FP-growth算法

相较于Apriori 算法：FP-growth算法对于挖掘长的短的频繁模式，都是有效和可以伸缩的，并比Apriopri算法快了1 个数量级；但当数据库很大时，构造基于内存的FP-tree 是不太现实的。

 

关于关联分析算法有一个非常有名的故事：”尿布和啤酒”。故事是这样的：美国的妇女们经常会嘱咐她们的丈夫下班后为孩子买尿布，而丈夫在买完尿布后又要顺手买回自己爱喝的啤酒，因此啤酒和尿布在一起被购买的机会很多。这个举措使尿布和啤酒的销量双双增加，并一直为众商家所津津乐道。

起初Apriori算法的提出有效的能发现这种物品间的关联规则，但是Apriori算法频繁的扫描数据集，造成效率低下，在大的数据集上执行的会非常缓慢。后来FP-Growth算法的提出有效的解决了这个缺点。

FP-Growth(Frequent Pattern Tree，频繁模式树)算法是韩家炜老师提出的关联分析算法，巧妙的将树型结构引入算法中，它采取如下分治策略：提供频繁项集的数据库压缩到一棵频繁模式树（FP-Tree），但仍保留项集关联信息；该算法和Apriori算法最大的不同有两点： 
第一，不产生候选集。 
第二，只需要两次遍历数据库，大大提高了效率。

流程如下： 
1：先扫描一遍数据集，得到频繁项为1的项目集，定义最小支持度（项目出现最少次数），删除那些小于最小支持度的项目，然后将原始数据集中的条目按项目集中降序进行排列。 
2：第二次扫描，创建项头表（从上往下降序），以及FP树。 
3：对于每个项目（可以按照从下往上的顺序）找到其条件模式基（CPB，conditional patten base）,递归调用树结构，删除小于最小支持度的项。如果最终呈现单一路径的树结构，则直接列举所有组合；非单一路径的则继续调用树结构，直到形成单一路径即可。

如果上述不是很明白的话，以下用图进行展示： 
如下图所示数据清单（第一列为购买id，第二列为物品项目）： 

第一步：构造FP树 
1：扫描事务数据库对每个物品进行记数: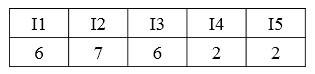 
 
2：定义minsup=20%，即最小支持度（物品最少出现的次数）为2。 
3：按照降序排列重新排列物品集。 
 
（如果出现小于2的物品则需要删除） 
4：按照项目出现次数重新调整数据库中的物品清单。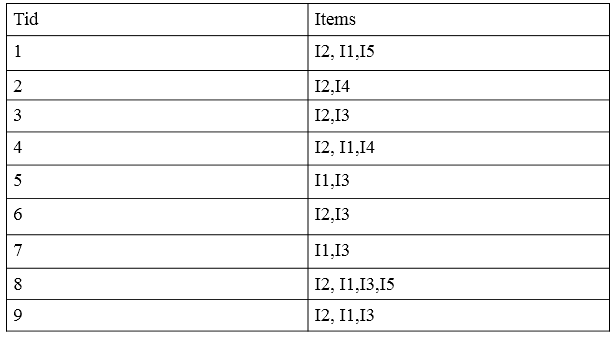 
 
5：进行FP树的构建： 
加入第一条清单（I2,I1,I5）：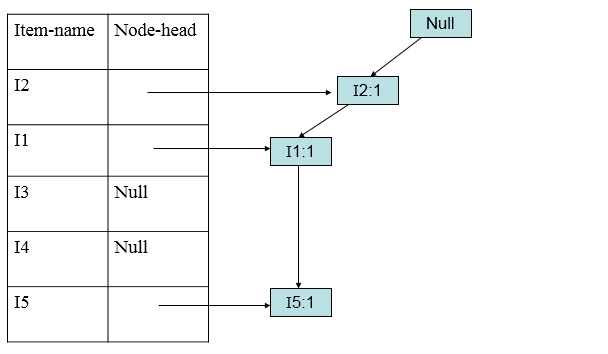 
 
加入第二条（I2,I4）： 
 
出现相同的节点要进行累加（I2）。 
加入第三条（I2,I3）： 
 
加入第四条（I2,I1,I4）：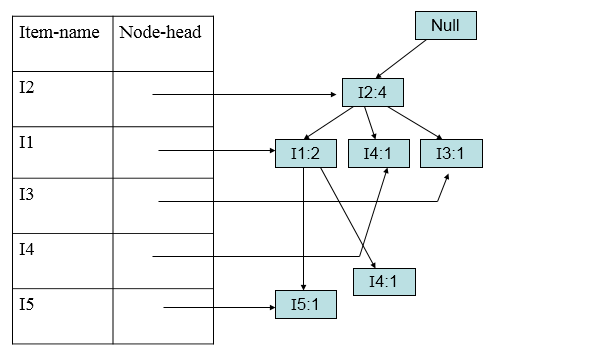 
 
加入第五条（I1,I3）：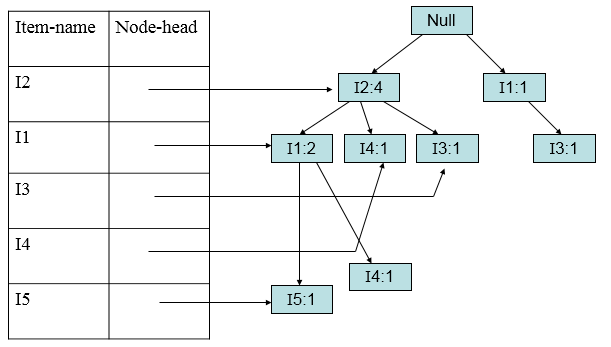 
 
加入第六条（I2,I3）：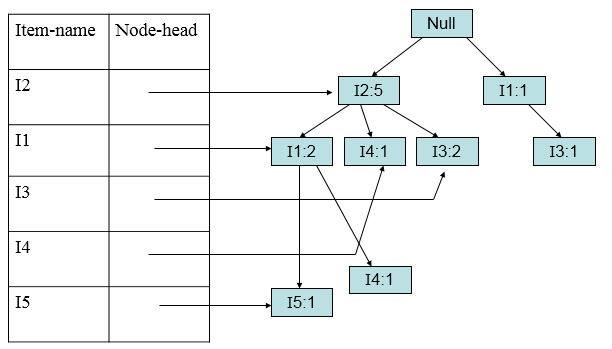 
 
加入第七条（I1,I3）： 
 
加入第八条（I2,I1,I3,I5）：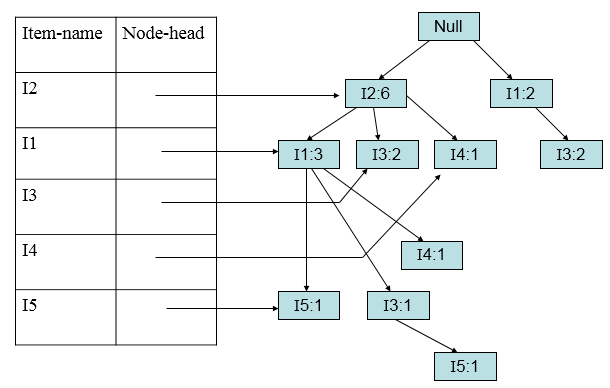 
 
加入第九条（I2,I1,I3）：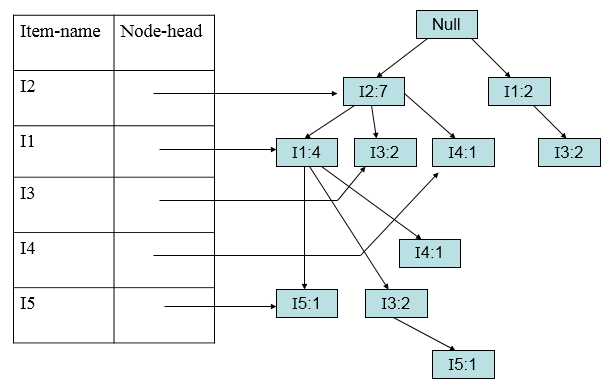 
 

这样FP树建立起来。

第二步：挖掘频繁项集 
可以按照从下往上的顺序: 先考虑I5： 
得到条件模式基<(I2,I1:1)>,<(I2,I1,I3:1)>,构造FP树： 
（条件模式基：顺着I5的链表，找出所有包含I5的前缀路径，这些前缀路径就是I5的条件模式基）。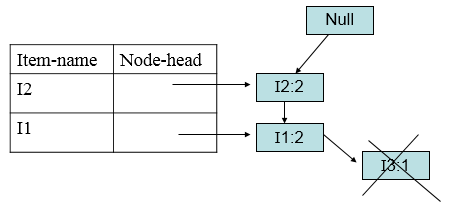 
 
删除小于支持度的节点。 
形成单条路径后进行组合。得到I5频繁项集：{{I2,I5:2},{I1,I5:2},{I2,I1,I5:2}}。 
接着考虑I4，得到条件模式基<(I2,I1:1)>、<(I2:1)>,构造条件FP树：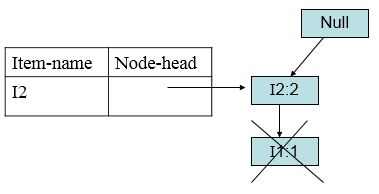 
 
得到I4频繁项集：{{I2,I4:2}}。 
然后考虑I3，得到条件模式基<(I2,I1:2)>、<(I2:2)>、<(I1:2)>构造条件FP树：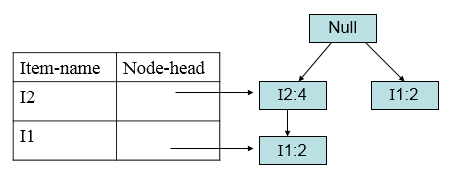 
 
由于此树不是单一路径，因此需要递归挖掘I3。 
递归考虑I3，此时得到I1条件模式基<(I2:2)>,即I1I3的条件模式基为<(I2:2)>构造条件FP树：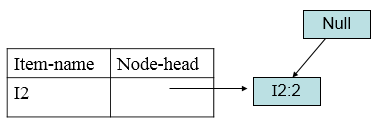 
 
得到I3的频繁项目集{{I2,I3:4},{I1,I3:4},{I2,I1,I3:2}}。 
最后考虑I1，得到条件模式基<(I2:4)>构造条件FP树：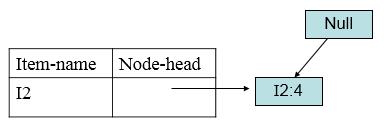 
 
得到I1的频繁项目集{{I2,I1:4}。

总结：FP-growth通过两次扫描数据库，将原始数据压缩在一个树形结构上，该树优点为路径共用，压缩数据，接着通过数找到每个item条件模式基，递归挖掘频繁项集，但不能用于发现关联规则。