关于Deeplearning中的激活函数梯度消失问题以及如何选择激活函数

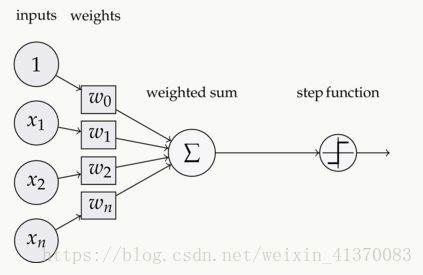
• 什么是激活函数？

如上：输入input,经过加权求和，再经过activation函数激活，再输出作为下一层的输入。

• 为什么要用激活函数

我们知道，经过加权求和时，输入呈现线性函数关系，此时如果没有激活函数，输出都呈现线性组合，不管神经网络有多少层，结果说到底为线性方程式，无法来映射现实中复杂的因素。之所以运用神经网络，是想让其能像人脑对外界复杂因素进行解析，而这些复杂因素往往并非简单线性所能解决。因此要对外界复杂因素的解析，就需要引入激活函数。激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

常见的激活函数有：sigmoid,tanh,Relu等

• 什么是梯度消失

梯度消失，常常发生在用基于梯度的方法训练神经网络的过程中。

当我们在做反向传播，计算损失函数对权重的梯度时，随着越向后传播，梯度变得越来越小，这就意味着在网络的前面一些层的神经元，会比后面的训练的要慢很多，甚至不会变化。

• 梯度消失的影响

我们知道网络开始的前面一些神经层，它们是整个网络的基础，负责学习和识别简单的模式，从而将学习和识别的模式一步步地传入下一层，倘若前面这些层他们的结果出现结果不准确的话，后面层也会受到相应的影响。甚至逐渐偏离我们想要的方向。

而且用基于梯度的方法训练出参数，主要是通过学习参数的很小的变化对网络的输出值的影响有多大。如果参数的改变，网络的输出值贡献很小，那么就会很难学习参数，花费时间是非常地长的。同时如果梯度迅速消失为0，我们可能将无法达到最优解或者局部最小值。

• 为什么会出现梯度消失（以下参考了慕课网老师的教程）

在训练神经网络时，为了让损失函数越来越小，其中一种优化的方法是梯度下降。梯度下降法简单的来说就是在权重的负梯度方向更新权重，如下面这个公式所示，一直到梯度收敛为零。在现实中我们会通过设定一个超参数叫做最大跌代数来控制，如果迭代次数太小，结果就会不准确，无法达到最优值或者局部最小值，如果迭代次数太大，那么训练过程会非常长。（个人在训练人脸比对时用FACENET，为了达到最优值，迭代次数迭代了30W次，耗时1000+个小时，同时也占用了公司服务器的大部分内存以及GPU的使用）

这里就需要计算参数的梯度，方法是用反向传播。

为了推导一下梯度消失的原因，我们来看一个最简单的神经网络的反向传播过程。

每个神经元有两个过程，一个是权重与上一层输出的线性组合，一个是作用激活函数。

来看一下最后的损失对第一层权重的梯度是怎样的：

其中各部分推导：

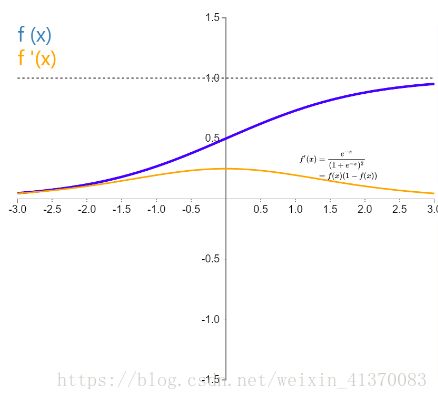
假设我们此时用的是sigmoid激活函数，那么我们来看看激活函数sigmoid以及其导数

同时一般情况下神经网络在权重初始化时，会按照高斯分布，平均值为0标准差为1这样进行初始化，所以权重矩阵也是小于1的。
于是可知道

由上面的例子可以看出，对第一层的权重求的偏导，就有五个小于1的数相乘，那么当层数越多，这就会以指数级迅速减小。

越靠前的层数，由于离损失越远，梯度计算式中包含的激活函数的导数就越多，那么训练也就越慢。

（那么梯度爆炸，也就是同样的道理，当激活函数的导数大于1的时候，它会呈指数级的增长。）

 

• 目前流行的解决方案

1.改变激活函数：

由前面的推导可以知道梯度消失的主要原因，是激活函数的导数小于 1，那么在选择激活函数时，就考虑这一点。

有哪些激活函数可以选择呢？

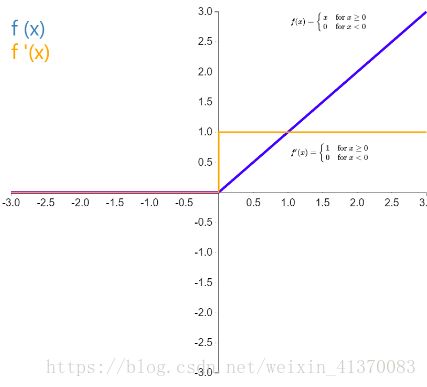
Relu

Rectified linear unit，x 大于 0 时，函数值为 x，导数恒为 1，这样在深层网络中使用 relu 激活函数就不会导致梯度消失和爆炸的问题，并且计算速度快。

但是因为 x 小于 0 时函数值恒为0，会导致一些神经元无法激活。

Leaky Relu，

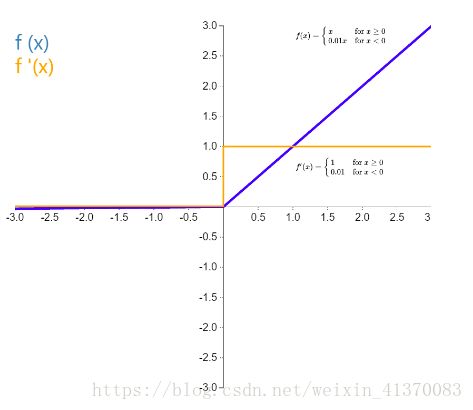
是 ReLU 激活函数的变体，为了解决 Relu 函数为 0 部分的问题，当 x 小于 0 时，函数值为 kx，有很小的坡度 k，一般为 0.01，0.02，或者可以作为参数学习而得。

优点
Leaky ReLU有ReLU的所有优点：计算高效、快速收敛、在正区域内不会饱和
导数总是不为零，这能减少静默神经元的出现，允许基于梯度的学习
一定程度上缓解了 dead ReLU 问题

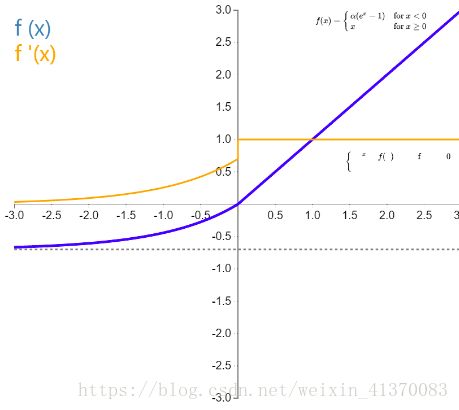
ELU

指数线性单元（Exponential Linear Unit，ELU）也属于 ReLU 的变体。x 小于 0 时为 alpha＊（e^x -1）和其它修正类激活函数不同的是，它包括一个负指数项，从而防止静默神经元出现，导数收敛为零，从而提高学习效率。

优点
不会有Dead ReLU问题
输出的均值接近0，zero-centered
缺点
计算量稍大

现在最常用的是 Relu，已经成了默认选择，
sigmoid 不要在隐藏层使用了，如果是二分类问题，可以在最后的输出层使用一下，
隐藏层也可以用 tanh，会比 sigmoid 表现好很多。

2.除了激活函数外的解决方案：

梯度消失：

• 逐层“预训练”（pre-training）＋对整个网络进行“微调”（fine-tunning）

• 选择合适的激活函数

• batch normalization 批规范化：通过对每一层的输出规范为均值和方差一致的方法，消除了 w 带来的放大缩小的影响

• 残差结构

• LSTM

梯度爆炸：

• 梯度剪切（ Gradient Clipping）

• 权重正则化

• 选择合适的激活函数

• batch normalization 批规范化，

• RNN 的 truncated Backpropagation through time ，LSTM

备注：以上是本人在做人脸比对项目时有关梯度消失问题的研究，同时参考了慕课网老师们的课件，所得出的感悟。如果存在知识点上的误导，希望大家可以email来联系我：[email protected]