医学图像分割模型的常用loss
1.交叉熵损失函数-cross entropy
- 二分类交叉熵损失函数binary_crossentropy
其中,N为像素点个数,
为输入实例
的真实类别,
为预测输入实例 属于类别 1 的概率. 对所有样本的对数损失表示对每个样本的对数损失的平均值, 对于完美的分类器, 对数损失为 0。
- 多分类交叉熵损失函数categorical_crossentropy
该损失函数分别检查每个像素，m为类别数(num_label),将类预测![y_{i}=[y_{i1},y_{i2},...,y_{im}]](http://img.e-com-net.com/image/info8/0829d2b940d3447a94a84aa603efcbf4.gif){kind=small}
(深度方向的像素向量)与我们的热编码目标向量![\hat{y}_{i}=[\hat{y}_{i1},\hat{y}_{i2},...,\hat{y}_{im}]](http://img.e-com-net.com/image/info8/cd94b9ce0fb0480cbc2b592337f06130.gif){kind=small}
进行比较。
由此可见，交叉熵的损失函数单独评估每个像素矢量的类预测，然后对所有像素求平均值，所以我们可以认为图像中的像素被平等的学习了。但是，医学图像中常出现类别不均衡（class imbalance）的问题，由此导致训练会被像素较多的类主导，对于较小的物体很难学习到其特征，从而降低网络的有效性。
pytorch代码实现
pytorch自带的nn.CrossEntropyLoss结合了nn.logSoftmax()和nn.NLLLoss()
class CrossEntropy(nn.Module):
def __init__(self,ignore_label=-1,weight=None):
super(CrossEntropy,self).__init__()
self.ignore_label=ignore_label
self.criterion=nn.CrossEntropyLoss(weight=weight,
ignore_index=self.ignore_label)
def forward(self, score,target):
'''
:param score: Tensor[bs,num_classes,256,256]
:param target: Tensor[bs,256,256]
:return:
'''
loss=self.criterion(score,target)
return loss2.带权重的交叉熵函数-Weighted cross entropy(WCE)
其中，![\omega=[\omega_{1},\omega_{2},...\omega_{m}]](http://img.e-com-net.com/image/info8/f340a620b1ff481fa6fcccdb37ecf35c.gif){kind=small}
为对预测概率图中每个类别的权重，用于加权在预测图上占比例小的类别对loss函数的贡献
3.Dice Coefficient Loss
dice coefficient 源于二分类，本质上是衡量两个样本的重叠部分。该指标范围从0到1，其中“1”表示完整的重叠。 其计算公式为：
其中
表示集合A、B 之间的共同元素，
表示 A 中的元素的个数，B也用相似的表示方法。
为了计算预测的分割图的 dice coefficient，将近似为预测图每个类别score和target之间的点乘，并将结果函数中的元素相加。
因为我们的目标是二进制的，因而可以有效地将预测中未在 target mask 中“激活”的所有像素清零。对于剩余的像素，主要是在惩罚低置信度预测; 该表达式的较高值（在分子中）会导致更好的Dice系数。
为了量化计算 和 
，部分研究人员直接使用简单的相加， 也有一些做法是取平方求和。
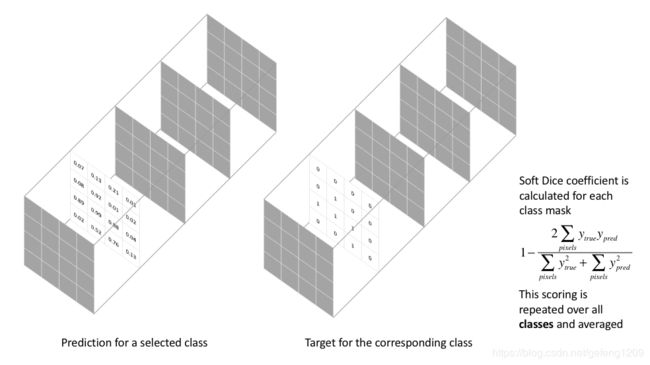
其中，在式子中 Dice系数的分子中有2，因为分母“重复计算” 了两组之间的共同元素。为了形成可以最小化的损失函数，我们将简单地使用1-Dice。这种损失函数被称为 soft dice loss，因为我们直接使用预测概率而不是使用阈值或将它们转换为二进制mask。
关于神经网络输出，分子涉及到我们的预测和 target mask 之间的共同激活，而分母将每个mask中的激活量分开考虑。实际上起到了利用 target mask 的大小来归一化损失的效果，使得 soft dice 损失不会难以从图像中具有较小空间表示的类中学习。
soft dice loss 将每个类别分开考虑，然后平均得到最后结果。
定义如下：
pytorch代码实现：
class SoftDiceLoss(nn.Module):
'''
Soft_Dice = 2*|dot(A, B)| / (|dot(A, A)| + |dot(B, B)| + eps)
eps is a small constant to avoid zero division,
'''
def __init__(self, weight=None):
super(SoftDiceLoss, self).__init__()
self.activation = nn.Softmax2d()
def forward(self, y_preds, y_truths, eps=1e-8):
'''
:param y_preds: [bs,num_classes,768,1024]
:param y_truths: [bs,num_calsses,768,1024]
:param eps:
:return:
'''
bs = y_preds.size(0)
num_classes = y_preds.size(1)
dices_bs = torch.zeros(bs,num_classes)
for idx in range(bs):
y_pred = y_preds[idx] #[num_classes,768,1024]
y_truth = y_truths[idx] #[num_classes,768,1024]
intersection = torch.sum(torch.mul(y_pred, y_truth),dim=(1,2)) + eps/2
union = torch.sum(torch.mul(y_pred, y_pred), dim=(1, 2)) + torch.sum(torch.mul(y_truth, y_truth), dim=(1, 2)) + eps
dices_sub = 2 * intersection / union
dices_bs[idx] = dices_sub
dices = torch.mean(dices_bs,dim=0)
dice = torch.mean(dices)
dice_loss = 1 - dice
return dice_loss
值得注意的是，dice loss比较适用于样本极度不均的情况，一般的情况下，使用 dice loss 会对反向传播造成不利的影响，容易使训练变得不稳定。有时使用dice loss会使训练曲线有时不可信，而且dice loss好的模型并不一定在其他的评价标准上效果更好，例如mean surface distance 或者是Hausdorff surface distance。不可信的原因是梯度，对于softmax或者是log loss其梯度简化而言为p−t，t为目标值，p为预测值。而dice loss为
，如果p，t过小则会导致梯度变化剧烈，导致训练困难。
4.IOU Loss
IOU类似于Dice，定义如下：
pytorch代码实现：
class SoftDiceLoss(nn.Module):
'''
Soft_Dice = 2*|dot(A, B)| / (|dot(A, A)| + |dot(B, B)| + eps)
eps is a small constant to avoid zero division,
'''
def __init__(self, weight=None):
super(SoftDiceLoss, self).__init__()
self.activation = nn.Softmax2d()
def forward(self, y_preds, y_truths, eps=1e-8):
'''
:param y_preds: [bs,num_classes,768,1024]
:param y_truths: [bs,num_calsses,768,1024]
:param eps:
:return:
'''
bs = y_preds.size(0)
num_classes = y_preds.size(1)
dices_bs = torch.zeros(bs,num_classes)
for idx in range(bs):
y_pred = y_preds[idx] #[num_classes,768,1024]
y_truth = y_truths[idx] #[num_classes,768,1024]
intersection = torch.sum(torch.mul(y_pred, y_truth),dim=(1,2)) + eps/2
union = torch.sum(torch.mul(y_pred, y_pred), dim=(1, 2)) + torch.sum(torch.mul(y_truth, y_truth), dim=(1, 2)) + eps
ious_sub = intersection / (union-intersection)
ious_bs[idx] = ious_sub
ious = torch.mean(ious_bs,dim=0)
iou = torch.mean(ious)
iou_loss = 1 - iou
return iou_lossIOU loss的缺点呢同DICE loss是相类似的，训练曲线可能并不可信，训练的过程也可能并不稳定，有时不如使用softmax loss等的曲线有直观性，通常而言softmax loss得到的loss下降曲线较为平滑。
5.Focal Loss
作者认为单级结构(YOLO,SSD)准确度低是由类别失衡(class imbalance)引起的。在深入理解这个概念前我们先来强化下“类别”这个概念：计算Loss的bbox可以分为positive和negative两类。当bbox(由anchor加上偏移量得到)与ground truth间的IOU大于上门限时(一般是0.5)，会认为该bbox属于positive example，如果IOU小于下门限就认为该bbox属于negative example。在一张输入image中，目标占的比例一般都远小于背景占的比例，所以两类example中以negative为主，这引发了两个问题：
１、negative example过多造成它的loss太大，以至于把positive的loss都淹没掉了，不利于目标的收敛；
２、大多negative example不在前景和背景的过渡区域上，分类很明确(这种易分类的negative称为easy negative)，训练时对应的背景类score会很大，换个角度看就是单个example的loss很小，反向计算时梯度小。梯度小造成easy negative example对参数的收敛作用很有限，我们更需要loss大的对参数收敛影响也更大的example，即hard positive/negative example。
这里要注意的是前一点我们说了negative的loss很大，是因为negative的绝对数量多，所以总loss大；后一点说easy negative的loss小，是针对单个example而言.
下图是hard positvie、hard negative、easy positive、easy negative四种example的示意图，可以直观的感受到easy negativa占了大多数。
二分类交叉熵定义损失如下：
可见普通的交叉熵对于正样本(positive)而言，输出概率越大损失越小。对于负样本(negative)而言，输出概率越小则损失越小。此时的损失函数在大量简单样本的迭代过程中比较缓慢且可能无法优化至最优.
Focal Loss定义如下：
是类别的预测概率，
是个大于0的值，
是个[0，1]间的小数，和都是固定值，不参与训练。从表达式可以看出：
1、对于前景类，越大，即越好预测，权重
就越小
对于背景类，越小，
越大，即越好预测，权重
就越小。
也就是说easy example可以通过权重进行抑制；
2、用于调节positive和negative的比例，前景类别使用时，对应的背景类别使用
；
3、和的最优值是相互影响的，所以在评估准确度时需要把两者组合起来调节。
目前在图像分割上只是适应于二分类。
代码：https://github.com/mkocabas/focal-loss-keras
from keras import backend as K
'''
Compatible with tensorflow backend
'''
def focal_loss(gamma=2., alpha=.25):
def focal_loss_fixed(y_true, y_pred):
#取前景后背景部分预测值，shape和y_true,y_pred相同
#取前景部分预测值，对背景忽略：设置为1
pt_1 = tf.where(tf.equal(y_true, 1), y_pred, tf.ones_like(y_pred))
#取背景部分预测值，对前景忽略：设置为0
pt_0 = tf.where(tf.equal(y_true, 0), y_pred, tf.zeros_like(y_pred))
return -K.sum(alpha * K.pow(1. - pt_1, gamma) * K.log(pt_1))-K.sum((1-alpha) * K.pow( pt_0, gamma) * K.log(1. - pt_0))
return focal_loss_fixed
使用方法：
model_prn.compile(optimizer=optimizer, loss=[focal_loss(alpha=.25, gamma=2)])
6.Generalized Dice loss
在使用DICE loss时，对小目标是十分不利的，因为在只有前景和背景的情况下，小目标一旦有部分像素预测错误，那么就会导致Dice大幅度的变动，从而导致梯度变化剧烈，训练不稳定。
GDL(the generalized Dice loss)公式如下：
在dice loss基础上增加了![\omega=[\omega_{1},\omega_{2},...,\omega_{m}]](http://img.e-com-net.com/image/info8/8ac845ae663848169fdfb83914387d82.gif){kind=small}
给每个类别加权，计算公式如下：
这样起到了平衡各类(包括背景类)目标区域对loss的贡献。
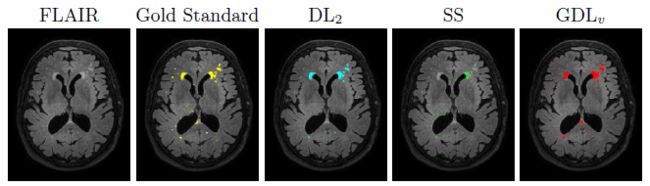
论文中的给出的分割效果：
但是在AnatomyNet中提到GDL面对极度不均衡的情况下，训练的稳定性仍然不能保证。
代码：
def generalized_dice_coeff(y_true, y_pred):
#y_true,y_pred shape=[num_label,H,W,C]
num_label=y_pred.shape[0]
w=K.zeros(shape=(num_label,))
w=K.sum(y_true,axis=(1,2,3))
w=1/(w**2+0.000001)
# Compute gen dice coef:
intersection_w = w*K.sum(y_true * y_pred, axis=[1,2,3])
union_w = w*K.sum(y_true+y_pred, axis=[1,2,3])
return K.mean( (2. * intersection_w + smooth) / (union_w + smooth), axis=0)
def generalized_dice_loss(y_true, y_pred):
return 1 - generalized_dice_coeff(y_true, y_pred)
未完待续......
参考：
医学图像分割常用的损失函数
从loss处理图像分割中类别极度不均衡的状况---keras
Focal Loss for Dense Object Detection解读