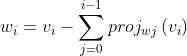彻底理解施密特正交化

在游戏编程中我们经常会用到施密特正交化，比如求解法线的切空间，我们需要把一组非正交的坐标系（ＮＢＴ），转换为正交的坐标系(N B’ T’）。

施密特正交化如何理解呢？我们先来看看官方给出的解释。

施密特正交化（Schmidt orthogonalization）是求欧氏空间正交基的一种方法。从欧氏空间任意线性无关的向量组α1，α2，……，αm出发，求得正交向量组β1，β2，……，βm，使由α1，α2，……，αm与向量组β1，β2，……，βm等价，再将正交向量组中每个向量经过单位化，就得到一个标准正交向量组，这种方法称为施密特正交化。

第一个问题什么是欧式空间？

游戏中所有向量的运算都是在欧式空间中，也就初中，高中学的向量空间都是欧式空间。

从起源来讲，欧式空间是满足欧几里得《几何原本》中几何五公理的空间。维基百科中给出的解释如下：

1. 从一点向另一点可以引一条直线。
2. 任意线段能无限延伸成一条直线。
3. 给定任意线段，可以以其一个端点作为圆心，该线段作为半径作一个圆。
4. 所有直角都相等。
5. 若两条直线都与第三条直线相交，并且在同一边的内角之和小于两个直角，则这两条直线在这一边必定相交。

第二个问题什么是线性无关向量组?

如果有向量组a1,a2,a3,...an，给定方程k1*a1+k2*a2+k3*a3+...+kn*an = 0，只存在唯一的一组解k1=k2=...=kn=0。那么该组向量就是线性无关向量组。

几何意义就是如果是二维向量组a1,a2，那么只要a1和a2不共边，他们就是线性无关向量组。

k1*a1 + k2*a2 = 0。假定a1和a2不是零向量且不共边，那么只有k1=k2=0，让a1和a2变成零向量，他们相加才会得0。否则两个非零且不共边的向量相加一定会得出一个新的非零向量。

共边向量相加可以得出零向量，比如两个方向相反且模一样的向量相加。

如果是三维向量组a1,a2,a3不共面，他们就是线性无关向量组。

如果a1,a2,a3共面的话根据共面向量定理a3 = x * a1 + y * a2。一定存在有序实数解x,y。

使得 x * a1 + y * a2 - a3 = 0。k1=x，k2 = y，k3 = -1。所以三个向量如果共面的话一定是线性相关的向量组。

如果三个向量不共面并且都不为零向量，那么他们相加一定会得出一个新的非零向量。所以只有通过k1=k2=k3=0，让a1,a2,a3变成零向量以后相加才能等于0。所以他们是线性无关向量组。

扩展到n维空间，也就是说如果一个向量组线性无关，那么其中任何一个向量都不能被其他向量线性表示。

比如在二维空间如果两个向量共边，那么这两个向量就可以乘以一个k来表示另外一个向量。

如果在三维空间如果三个向量共面，那么就存在一组有序的实数(x,y)分别乘上两个向量来表示另外一个向量。

换句话说向量组中的每个向量都是不能被其他向量替代的，那么这组向量就是线性无关向量。

接下来我们看看施密特正交化定义。

给定一组线性无关的向量组α1，α2，……，αm。根据这组向量我们其实可以定义一个m维的空间坐标系。只不过他们不是两两正交的坐标系。我们希望通过施密特正交化，求出一组正交坐标系β1，β2，……，βm，使得这两组坐标系等价。

什么是向量组等价，两个向量组可以互相线性表示。我们就说这两个向量组等价。下面我们给出施密特正交化的公式。

给定一组线性无关向量组{v0,...vn}，我们通过施密特正交化将其转换为一组正交化向量组{w0,...wn}的步骤是：

公式看上去很复杂，理解其中的几何意义后就不复杂了。

已知一个向量v和一个单位向量n，那么向量v在单位向量n上的投影向量就是这两个向量的点积

如果向量n不是单位向量，我们只需要把n变成单位向量即可，那么向量v在向量n上的投影向量为

向量w = v-p就能得到一个垂直的向量w。

对于二维空间中v0,v1它的正交向量组w0,w1就是。

令

 

三维向量同理附上一张贴图方便理解

 

以此类推就能理解斯施密特正交化的过程了。