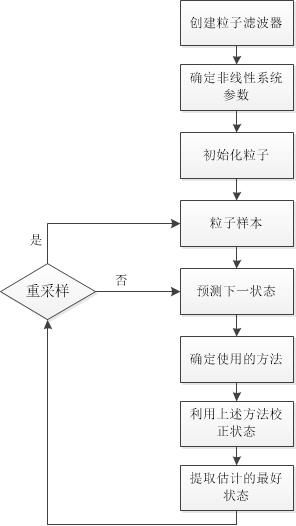
粒子滤波流程

粒子滤波算法递归地计算状态估计，包括两个步骤：

1、预测：算法利用给出的系统模型，由前一时刻的状态估计现在时刻的状态；

2、校正：算法利用当前感知方法去校正状态估计。

想要正确的使用粒子滤波，你必须确定如下参数：粒子数量，初始目标区域，状态估计方法。此外，如果你有特定的运动和感知模型，则分别在状态转换函数和测量似然函数中指定这些参数。想要更多信息，请参考粒子滤波参数（粒子滤波参数）。

下面是使用粒子滤波的基本流程图。本文详细介绍了预测估计流程，并且显示了如何在循环中运行粒子滤波以及连续状态估计的示例。

一、估计流程图

二、具体过程

创建粒子滤波器：

调用 robotics.ParticleFilter(点击打开链接)

设置非线性系统参数：

将这些粒子滤波器参数的参数设置为你自己具体的系统或者应用的参数，

StateTransitionFcn

MeasurementLikelihoodFcn

ResamplelingPolicy

ResamplelingMethod

StateEstimationMethod

默认给出的参数用于基本操作。StateTransitionFcn和MeasurementLikelihoodFcn函数定义为系统行为和方法集成。它们对于粒子滤波跟踪准确性非常的重要。想要了解更多，请参考Particle Filter Parameters.

初始化粒子：

利用初始化的方法设置粒子数量和初始状态。见robotics.ParticleFilter.initialize(点击打开链接)

分布的样本粒子：

你可以用两种方法采样初始化粒子位置，

1）、初始姿态和协方差——如果你确定你的初始化状态的ideas，这种方法则需要你明确你的初始位姿和协方差。此方法有助于将粒子聚集到更接近你的估   计，因此跟踪从一开始就更加有效；

2）、状态边界——如果你不知道你的初始状态，你可以指定每个状态变量的边界。粒子均匀的分布在每个变量的状态边界上。在跟踪过程中，大量分布的粒   子是无效的，只有很少一部分处于实际状态附近。使用状态边界，通常需要更多的粒子，计算时间和迭代来收敛到实际的状态估计。

预测：

根据具体的状态转移方程，粒子演化以估计下一状态。使用predict执行StateTransitionFcn属性中指定的状态转换函数。见robtics.ParticleFilter.predict(点击打开链接)

确定使用的方法：

由传感器收集的测量值用于下一步骤以校正当前预测状态。

校正：

使用测量值来调整预测状态并校正估计。使用正确的函数进行测量。robotics.ParticleFilter.correct(点击打开链接)使用MeasurementLikehoodFcn来计算每个粒子 的传感器测量可能性。粒子重采样要求更新在后续迭代中状态的改变。此步骤基于ResamplingMethod和ResamplingPolicy属性触发重采样。

提取最好的状态估计：

在校正之后，基于每个粒子的权重和robotics.ParticleFilter(点击打开链接)里面的属性StateEstimationMehod来进行自动提取最优状态估计。最优状态估计和协方 差来自于校正方程的输出。

重采样：

这一步不是分来调用的，而是在你调用校正时执行的。一旦状态充分改变，那么就要基于最新的估计重采样你的粒子。正确的方法会根据粒子当前分布及其权重触 发重采样来检查ResamplingPolicy。如果重采样没有被触发，相同的粒子会被用于下一状态的估计。如果你的装填变化不大，或者时间步长低，你可以调用 predict和correct方法，而不用重采样。

持续估计和校正：

重复预测和校正步骤是估计状态所必须的。校正步骤确定重采样步骤是否为必要的。以下情况时，多次调用预测和校正是必要的：

1）、没有可用的测量值，而控制输入和时间的更新以高频率在发生。使用预测方法演化粒子以更频繁地获得更新的预测状态；

2）、多测量读数可用。利用校正去触发从相同的或多传感器中读取数据。方程根据每一个收集的数据集去校正状态。

三、利用粒子滤波估计机器位置

利用粒子滤波去跟踪一个2维空间的机器。这个要目标位置随机添加了一些噪音。利用预测和校正，根据这个方法和一个假设运动模型来跟踪机器。

初始化粒子滤波器、确定默认状态转移方程、测量似然方程、重采样策略。

pf=robotics.ParticleFilter;

pf.StateEstimationMethod='mean';

pf.ResamplingMetod='systematic';

1000个样本粒子的初始位置为[0 0]，并且归一化协方差。

initialize(pf,1000,[0 0],eye(2));

在估计之前，先定义一个用于跟踪的正弦波路径。创建一个数组，用于存放预测和估计的位置。定义噪声幅度。

t=0:0.1:4*pi;

dot=[t; sin(t)]' :

robotPred=zeros(length(t),2);

robotCorrected=zeros(length(t),2);

noise=0.1;

根据测量值，开始预测和校正估计位置。根据Resampling属性进行粒子重采样。机器根据加了随机噪音的正弦波函数移动。

for i=1:length(t)

%预测下一位置。如果需要，则进行重采样

[robotPred(i,:),robotCov]=predict(pf);

%生成随机噪音

measurement(i, :)=dot(i, :)+noise*(rand([1 2])-noise/2);

%根据给出的测量值纠正位置以获取最优估计

%事实上点的位置是没有用的。用数组保存校正的位置

[robotCorrected(i , :),robotCov]=correct(pf,measurement(i,:));

end

对比估计位置画出真实轨迹。事实上，由于粒子的随机分布，结果可能有多种。

plot(dot(:,1),dot(:,2),robotCorrected(:,1),robotCorrected(:,2),'or')

xlim([0 t(end)])

ylim([-1 1])

legend('Actual position','Estimated position')

grid on

画出图像后，我们会发现，估计的机器运动轨迹和真实的轨迹是很相似的。

本文参考链接地址：

https://cn.mathworks.com/help/robotics/ug/particle-filter-workflow.html