LeetCode学习笔记——最小覆盖串/字母异位词（Sliding Window)

个人博客：The Blog Of WaiterXiaoYY 欢迎来互相交流学习。

找子串，选滑动窗口

从一个字符串中找出符合条件的字串，一般会想到滑动窗口，

今天总结两道题，套路是差不多的，也算是滑动窗口的经典问题，

一道是最小覆盖子串，一道是找到字符串中所有的字母异位词，

具体等会我们再说。

这两道题的思路是差不多的，

大概就是窗口的右边界一直移动，直到要求的字符纳入到窗口中，

然后开始移动左边界，左边界增加缩短窗口，等到该窗口不再符合要求，就是我们要求的结果，

下面，我们具体看看。

最小覆盖子串

给你一个字符串 S、一个字符串 T，请在字符串 S 里面找出：包含 T 所有字母的最小子串。

示例：

输入: S = "ADOBECODEBANC", T = "ABC"
输出: "BANC"

说明：

• 如果 S 中不存这样的子串，则返回空字符串 ""。
• 如果 S 中存在这样的子串，我们保证它是唯一的答案。

题目的意思是，从s中找出包含T的字串，然后这个字串得最小，

毫无疑问，这个子串的两边都是来自T里面的字符，

我们需要做的是确定这个这个子串的起始位置，还有这个字串的长度，这样子我们就可以直接从母串S中返回这个子串，

已经知道我们要用滑动窗口来做，滑动窗口是这样的，

我们需要两个指针，这两个指针代表的是窗口的边界，

他们的差值就是窗口的长度，也是子串的长度，

这个窗口并不是一开始就固定不变的，

因为我们并不能一开始就确定长度，所以这个窗口的长度是慢慢变大的，

在变大的同时也将纳入字符，

这时候我们还需要两个哈希表，

一个哈希表用来记录T里面字符的数量，表示我们的需求，

另一个哈希表记录的是我们窗口里面出现我们需求字符的数量，

如果两者一致了，则说明这个窗口已经将我们所需求的全部字符纳入了，

这是一个合格的窗口，但它不是一个最短窗口，

我们需要缩短这个窗口的长度，前面我们说了，最短字串的两边一定是T里面的字符，

所以此时右边界的字符一定是我们需求里面的最后一个字符，也就是右边界已经达到最大了，

但左边界还不一定，

这时候就需要我们移动左边界，当移动到我们需求的第一个字符的时候，就表示左边界达到了最大，

这时候右边界和左边界的差值就是我们的所要求的字串长度。

但此字串长度未必是我们结果，

因为也许还会有更短的，所以我们需要不断重复以上操作，去求所有结果里面的最小值，才是我们最终的结果。

以上就是这道题的思路，上面详细叙述了整个过程，如果你还不是很懂，就看下面的图文吧！

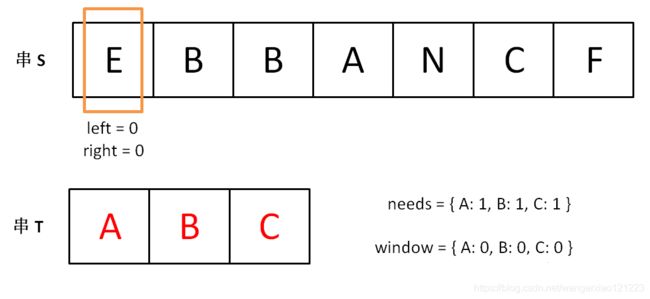
needs 和 window是我们两个计数的哈希表，

needs统计T中的字符数量，也就是我们的需求，

window 统计此时窗口中我们需求字符的数量，

初始状态：

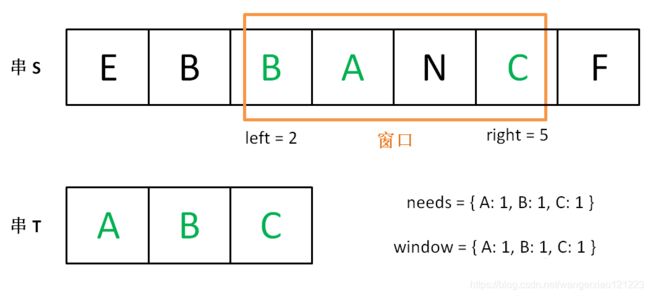
增加right，直到窗口[left, right]包含了T中所有的字符，右边界此时达到最大，

现在开始增加left，缩小窗口[left, right]，直到窗口的两边边界都为T中的元素，且窗口内的字符数量与需求的数量一致，

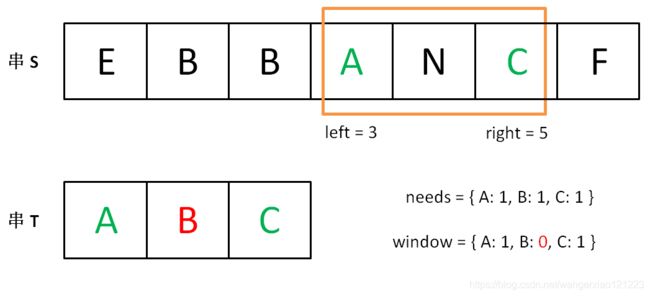
继续移动窗口左边界，直到窗口不再合格

之后重复以上过程，直到right 达到字符串 S的右边界，此时返回所有窗口的最小值。

如果能够明白这些，我们可以尝试来写一下我们的伪代码：

//两个字符串
String s,t;

//左边界和右边界
int left = 0, right = 0;
String res = s;

while(right < s.length()) {
    window.put(窗口的右边界);
    right++;
    如果窗口符合要求，此时移动左边界缩小窗口
    while(window 符合要求) {
        res = min(res, window);
        将window里左边界对应的符合要求的字符数量置为0;
        left++;
    }
}
return res;

哈希表window中存放的是字符串t中的对应的字符的数量，而不是窗口中所有出现的字符的数量，这点明确，再加上上面的伪代码可以理解了，我们就可以直接写出我们的最终代码了。

代码

class Solution {
    public String minWindow(String s, String t) {
        //两个哈希表用于计数
        HashMap<Character, Integer> window = new HashMap<>();
        HashMap<Character, Integer> need = new HashMap<>();
        //左右边界
        int left = 0;   
        int right = 0;
        //count用于统计window中的字符数量是否已经符合需求了
        int count = 0;
        //记录找到符合要求开始的字符位置
        int start = 0;
        int minlen = Integer.MAX_VALUE;
        //将字符串t的字符统计出来，作为我们的需求
        for(char c : t.toCharArray())
            need.put(c, need.getOrDefault(c, 0) + 1);
        //开始扩大窗口
        while(right < s.length()) {
            char c1 = s.charAt(right);
            //如果此字符串是我们需求的字符串
            if(need.containsKey(c1)) {
                //则加入到window中
                window.put(c1, window.getOrDefault(c1, 0) + 1);
                //对比两个哈希表中此字符的数量，如果相等，说明此字符满足我们需求了
                if(window.get(c1).equals(need.get(c1)))
                    count++;
            }
            right++;
            //当我们的需求的字符数量全部出现再这个窗口时，开始移动左边界缩小窗口
            while(count == need.size()){
                //如果窗口的大小小于最小值，则更新，并记录此时的位置，即窗口的开始的位置，也是字符串的开始位置
                if(right - left < minlen) {
                    start = left;
                    minlen = right - left;
                }
                //此时判断左边界的字符是否为我们的需求
                char c2 = s.charAt(left);
                if(need.containsKey(c2)) {
                    //如果符合，则将window中对应字符的数量减少
                    window.put(c2, window.getOrDefault(c2, 0) - 1);
                    //如果window中的字符数量已经少于需求数量，则count减少
                    if((int)window.get(c2) < (int)need.get(c2))
                        count--;
                }
                left++;
            }
        }
        //返回字符串
        return minlen == Integer.MAX_VALUE ? "" : s.substring(start, start + minlen);
    }
}

对于代码中有几处比较巧妙的地方，

一个是：

minlen = right - left;

窗口的长度等于right - left，这点母庸质疑，但其实这不是严格意义上的窗口位置，也就是说，right其实不是窗口的右边界，left也不是窗口的左边界，但是这样是没有错的。

因为在移动窗口的的时候，right和left都相应的加一，其实指向的是我们所认为的窗口边界的下一个字符。

第二个是：

if((int)window.get(c2) < (int)need.get(c2))  count--;

此时用了（int）进行强转，这里涉及到Integer的装箱拆箱的知识，

在没有加（int）的之前，面对相对比较短的字符串，没有问题，

但测试案例中有很长的字符串，当字符数量大于128时，此时java的Integer是自动装箱，

而Integer此时不能拆箱，所以要用（int）拆箱才能进行比较。

第三个是：

return minlen == Integer.MAX_VALUE ? "" : s.substring(start, start + minlen);

这里主要对结果的处理，利用String类里面的substring()方法返回字符串中想要的开始位置和长度。

找到字符串中所有的字母异位词

给定一个字符串 s 和一个非空字符串 p，找到 s 中所有是 p 的字母异位词的子串，返回这些子串的起始索引。

字符串只包含小写英文字母，并且字符串 s 和 p 的长度都不超过 20100。

说明：

• 字母异位词指字母相同，但排列不同的字符串。
• 不考虑答案输出的顺序。

示例 1:

输入:
s: "cbaebabacd" p: "abc"

输出:
[0, 6]

解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的字母异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的字母异位词。

示例 2:

输入:
s: "abab" p: "ab"

输出:
[0, 1, 2]

解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的字母异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的字母异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的字母异位词。

这道题和上面那道题是很相似的，如果看懂了上面那道题，其实完全可以做这道题了，

我们再来分析一下这道题，

找字串问题，首先想滑动窗口，

在s中找出对应p的子串，但字母的顺序可以不同，返回每个子串开始的位置，

那我们照样可以用两个哈希表来记录窗口中需求的字符数量和我们需求的字符数量，

这道题和上道题不同，上道题窗口中可以有不是我们需求的字符，但这道题中窗口的字符一定是我们需求的字符才可以，

所以我们只需要找到字符数量相等了，此时的起点位置就是我们的结果，我们需要用一个列表来记录我们的结果，

结合以上，直接上代码了，

代码

class Solution {
    public List<Integer> findAnagrams(String s, String p) {
        //用一个列表来记录我们的结果
        List<Integer> res = new ArrayList<>();
        //两个哈希表用于计数
        HashMap<Character, Integer> window = new HashMap<>();
        HashMap<Character, Integer> need = new HashMap<>();
        //左右边界
        int left = 0;   
        int right = 0;
        //count用于统计window中的字符数量是否已经符合需求了
        int count = 0;
        //记录找到符合要求开始的字符位置
        int start = 0;
        //将字符串t的字符统计出来，作为我们的需求
        for(char c : t.toCharArray())
            need.put(c, need.getOrDefault(c, 0) + 1);
        //开始扩大窗口
        while(right < s.length()) {
            char c1 = s.charAt(right);
            //如果此字符串是我们需求的字符串
            if(need.containsKey(c1)) {
                //则加入到window中
                window.put(c1, window.getOrDefault(c1, 0) + 1);
                //对比两个哈希表中此字符的数量，如果相等，说明此字符满足我们需求了
                if(window.get(c1).equals(need.get(c1)))
                    count++;
            }
            right++;
            //当我们的需求的字符数量全部出现再这个窗口时，开始移动左边界缩小窗口
            while(count == need.size()){
                //此时窗口的长度等于p的长度，则说明该窗口符合，加入到结果中
                if(right - left == p.length()) {
                    res.add(left);
                }
                //此时判断左边界的字符是否为我们的需求
                char c2 = s.charAt(left);
                if(need.containsKey(c2)) {
                    //如果符合，则将window中对应字符的数量减少
                    window.put(c2, window.getOrDefault(c2, 0) - 1);
                    //如果window中的字符数量已经少于需求数量，则count减少
                    if((int)window.get(c2) < (int)need.get(c2))
                        count--;
                }
                left++;
            }
        }
        return res;
    }
}

---

整理完于2020.4.7，本文参考于 labuladong 的文章，文中图片源自 labuladong的算法小抄，只为学习而用，侵删。