【读书笔记】《算法竞赛进阶指南》读书笔记——0x40数据结构进阶

记录一下自己刷《算法竞赛进阶指南》的过程，梦想还是要有的 ╯︿╰

---

并查集（Disjoint-Set）

路径压缩：采取路径压缩优化的并查集，每一次查询操作的均摊复杂度为$O(logN)$

按秩合并：秩一般有两种定义：
1. 树的深度（未压缩路径时）
2. 集合的大小

无论采取哪种定义，都可以把“集合的秩”储存在“代表元素”，也就是树根上，在合并时把秩较小的树根作为秩较大的树根的子节点。

值得一提的是，当把“秩”定义为集合的大小时，“按秩合并”也被称为“启发式合并”，他是数据结构相关问题中的一种重要思想，启发式合并的原则是，把较小的结构合并到较大的结构中，并且只增加小的结构的查询代价。

采用按秩合并的并查集，每一次查询操作的均摊复杂度为$O(logN)$

同时采用路径压缩和按秩合并的并查集，每一次查询操作的均摊复杂度可以进一步降低到$O(\alpha (N))$，其中$\alpha (N)$称为反阿克曼函数，是一个比$\log (N)$增长还慢的函数，近似为常数（由Tarjan证明）

实际应用中，一般只用路径压缩优化就够了。

例题：POJ 1456 Supermarket

使用贪心和并查集；
把商品按利润从大到小排序，建立一个关于过期日期的并查集，起初每一天各自构成一个集合，对于每一个商品，若它在$d$天之后过期，就在并查集中查询树根（记为$r$），若$r$大于$0$，就把该商品安排在第r天，同时让$r$成为$r-1$的子节点，累积答案。

struct pro
{
    int val;
    int day;
    friend bool operator<(pro p1, pro p2)
    {
        return p1.val > p2.val;
    }
};

pro prod[10005];
int father[10005], n;

void init()
{
    for (int i = 0; i <= 10002; ++i)
        father[i] = i;
}

int getFather(int son)
{
    if (father[son] == son) return son;
    else return father[son] = getFather(father[son]);
}

int main()
{
    cin.sync_with_stdio(false);
    cin.tie(0);

    while (cin >> n)
    {
        init();
        for (int i = 0; i < n; ++i)
            cin >> prod[i].val >> prod[i].day;

        int ans = 0;
        sort(prod, prod + n);

        for (int i = 0; i < n; ++i)
        {
            int fa = getFather(prod[i].day);
            if (fa > 0)
            {
                ans += prod[i].val;
                father[getFather(fa)] = getFather(fa - 1);
            }
        }

        cout << ans << endl;
    }
}

这两个代码的耗时竟然是一样的(+_+)?

struct pro
{
    int val;
    int day;

    friend bool operator<(pro p1, pro p2)
    {
        return p1.val < p2.val;
    }
};

int father[10000 + 5], n;

void init()
{
    for (int i = 0; i <= 10000 + 2; ++i)
        father[i] = i;
}

int getFather(int son)
{
    if (father[son] == son) return son;
    else return father[son] = getFather(father[son]);
}

int main()
{
    cin.sync_with_stdio(false);
    cin.tie(0);

    while (cin >> n)
    {
        init();

        pro p;
        priority_queue <pro> q;
        for (int i = 0; i < n; ++i)
        {
            cin >> p.val >> p.day;
            q.push(p);
        }

        int ans = 0;
        while (!q.empty())
        {
            p = q.top();
            q.pop();

            int fa = getFather(p.day);
            if (fa > 0)
            {
                ans += p.val;
                father[getFather(fa)] = getFather(fa - 1);
            }
        }

        cout << ans << endl;
    }
}

“扩展域”与“边带权”的并查集

边带权的并查集：

并查集实际上是由若干棵树构成的森林，偶们可以在树中的每条边上记录一个权值，即维护一个数组$d$，用$d[x]$保存$x$到父节点$fa[x]$之间的边权，在每次路径压缩后，更新这些节点的$d$值。

例题： CH4101 银河英雄传说

自己的代码，未关流，2008ms
书本资料里的标称，744ms
自己的代码，关流，864ms

const int MAX = 30005;

// father[x]记录x的父节点，dis[x]记录x到根节点的距离，num[x]记录x为树根的集合大小
int father[MAX], dis[MAX], num[MAX];

void init()
{
    for (int i = 0; i < MAX; ++i)
    {
        father[i] = i; // 初始化
        dis[i] = 0;
        num[i] = 1;
    }
}

int getFather(int son)
{
    if (son != father[son])
    {
        int root = getFather(father[son]); // 递归计算集合代表

        dis[son] += dis[father[son]]; // 对边权求和

        father[son] = root; // 路径压缩
    }
    return father[son];
}

void merge(int x, int y)
{
    x = getFather(x);
    y = getFather(y);

    father[x] = y;
    dis[x] = num[y];
    num[y] += num[x];
}

int main()
{
    cin.sync_with_stdio(false);
    cin.tie(0);
    int cases;

    while (cin >> cases)
    {
        init();
        char cmd;
        int i, j;

        while (cases--)
        {
            cin >> cmd >> i >> j;

            if (cmd == 'M')
            {
                merge(i, j);
            }
            else
            {
                if (getFather(i) != getFather(j))
                    cout << -1 << endl;
                else
                    cout << abs(dis[i] - dis[j]) - 1 << endl;
            }
        }
    }
}

书本标称：

int n;
int p[30010], dis[30010], size[30010];
int find(int k)
{
	if (p[k] != k)
	{
		int f = find(p[k]);
		dis[k] += dis[p[k]];
		p[k] = f;
	}
	return p[k];
}
int main()
{
	for (int i = 1; i <= 30000; i++)
	{
		size[i] = 1;
		p[i] = i;
	}
	scanf("%d", &n);
	while (n--)
	{
		char s[2];
		int x, y;
		scanf("%s", s);
		scanf("%d%d", &x, &y);
		int fi = find(x), fj = find(y);
		if (s[0] == 'M')
		{
			p[fi] = fj;
			dis[fi] = size[fj];
			size[fj] += size[fi];
		}
		else
		{
			if (fi != fj)  printf("-1\n");
			else printf("%d\n", abs(dis[x] - dis[y]) - 1);
		}
	}
	return 0;
}

例题： POJ 1733 Parity Game

首先，因为题目里的$N$很大，需要对每一次询问的$left$和$right$进行离散化，使其范围缩小到$[0,2M]$内；
边权为$0$时表示奇偶性相同，边权为$1$时代表奇偶性不同，这样在路径压缩的时候使用异或$(xor)$运算就可以很方便的实现奇偶性的合并；
对于每一个询问，先检利用并查集查左节点和右节点是否在同一集合内（即当前的区间是否已经由之前的询问而已知）；
如果不在同一个集合内，则合并两个节点，异或运算大法；
如果在同一个集合内，验证$val[x](xor)val[y]$和题目给出的情况是否符合；

struct q
{
    int left; // 区间左端
    int right; // 区间右端
    int ans; // 记录奇偶性
} query[10005];

int arr[10005], // 离散化之后的数组
    val[10005], // 记录奇偶性（边的权值）
    father[10005], // 父节点
    n, m; // 题目里的n和m

void init()
{
    for (int i = 0; i < 10005; ++i)
    {
        val[i] = 0; // 初始化
        father[i] = i;
    }
}

int getFather(int son)
{
    if (father[son] != son)
    {
        int root = getFather(father[son]); // 找到根节点
        val[son] ^= val[father[son]]; // 合并权值
        father[son] = root; // 路径压缩
    }
    return father[son];
}

int main()
{
    while (cin >> n >> m)
    {
        int t = 0;
        char s[10];
        init();

        for (int i = 0; i < m; ++i) // 读入数据
        {
            cin >> query[i].left >> query[i].right >> s;

            if (s[0] == 'o')
                query[i].ans = 1; // 奇数
            else
                query[i].ans = 0; // 偶数

            arr[++t] = query[i].left - 1; // 为离散化做准备
            arr[++t] = query[i].right;
        }

        sort(arr, arr + t); // 离散化
        n = int(unique(arr, arr + t) - arr); // STL的unique函数

        int ans = m;
        for (int i = 0; i < m; ++i)
        {   // STL的lower_bound
            int x = int(lower_bound(arr, arr + n, query[i].left - 1) - arr);
            int y = int(lower_bound(arr, arr + n, query[i].right) - arr); // 找到离散化之后的值

            int fx = getFather(x); // 查询父节点
            int fy = getFather(y);

            if (fx == fy)
            {
                if (val[x] ^ val[y] != query[i].ans) // 是否说谎
                {
                    ans = i;
                    break;
                }
            }
            else
            {
                father[fx] = fy; // 合并节点
                val[fx] = val[x] ^ val[y] ^ query[i].ans;
            }
        }
        cout << ans << endl;
    }
}

使用“扩展域”的并查集

对于POJ 1733 Parity Game：
把每一个变量$x$拆成两个节点$x_{odd}$和$x_{even}$，其中$x_{odd}$表示$sum[x]$是奇数，$x_{even}$表示$sum[x]$是偶数；也经常将这两个节点称为$x$的奇数域和偶数域；

对于每个问题，设离散化后$left-1$和$right$的值分别为$x$和$y$，设$ans$表示该问题的回答，（0代表偶数个，1代表奇数个）；

1. 若$ans=0$，则合并$x_{odd}$与$y_{odd}$，$x_{even}$与$y_{even}$，这表示“x为奇数”与“y为奇数”可以互相推出，“x为偶数”与“y为偶数”可以互相推出，它们是等价的；

2. 若$ans=1$，则合并$x_{odd}$与$y_{even}$，$x_{even}$与$y_{odd}$，这表示“x为奇数”与“y为偶数”可以互相推出，“x为偶数”与“y为奇数”可以互相推出，它们是等价的；

上述合并同时还维护了关系的传递性，比如，在处理完$(x,y,0)$与$(y,z,1)$之后，x和z之间的关系也就已知了；

这种做法就相当于在无向图上维护节点之间的联通情况，只是扩展了多个域来应对多种传递关系；

使用扩展域并查集解决POJ 1733 Parity Game：

const int MAX = 10005;

struct q
{
    int left;
    int right;
    int ans;
} query[MAX];

int discrete[MAX * 2], father[4 * MAX], n, m;

void init()
{
    for (int i = 0; i < 4 * MAX; ++i)
        father[i] = i;
}

int getFather(int son)
{
    if (father[son] == son) return son;
    else return father[son] = getFather(father[son]);
}

int main()
{
    while (cin >> n >> m)
    {
        init();
        int t = 0;
        char s[10];

        for (int i = 0; i < m; ++i)
        {
            cin >> query[i].left >> query[i].right >> s;

            discrete[t++] = query[i].left - 1;
            discrete[t++] = query[i].right;

            if (s[0] == 'o')
                query[i].ans = 1;
            else
                query[i].ans = 0;
        }

        sort(discrete, discrete + t); // 传说中的离散化
        n = int(unique(discrete, discrete + t) - discrete);

        int ans = m;
        for (int i = 0; i < m; ++i)
        {
            int x = int(lower_bound(discrete, discrete + n, query[i].left - 1) - discrete);
            int y = int(lower_bound(discrete, discrete + n, query[i].right) - discrete);

            int x_odd = x;
            int x_even = x + n;
            int y_odd = y;
            int y_even = y + n;

            if (query[i].ans == 0) // 回答奇偶性相同
            {
                if (getFather(x_odd) == getFather(y_even))
                {
                    ans = i;
                    break;
                }
                else
                {
                    father[getFather(x_odd)] = getFather(y_odd);
                    father[getFather(x_even)] = getFather(y_even);
                }
            }
            else // 回答奇偶性不同
            {
                if (getFather(x_odd) == getFather(y_odd))
                {
                    ans = i;
                    break;
                }
                else
                {
                    father[getFather(x_odd)] = getFather(y_even);
                    father[getFather(x_even)] = getFather(y_odd);
                }
            }
        }

        cout << ans << endl;
    }
}

例题： POJ 1182 食物链

把每个动物$x$拆为同类域$x_{self}$、捕食域$x_{eat}$、天敌域$x_{enemy}$；

若一句话说“x与y为同类”，则说明“x的同类”与“y的同类”一样、“x的捕食物种”与“y的捕食物种”一样、“x的天敌”与“y的天敌”一样，此时，合并$x_{self}$与$y_{self}$、$x_{eat}$与$y_{eat}$、$x_{enemy}$与$y_{enemy}$；

若一句话说“x吃y”，则说明“x的捕食物种”就是“y的同类”、“x的同类”就是“y的天敌”，“x的天敌”就是“y的捕食物种“，此时应该合并$x_{eat}$与$y_{self}$、$x_{self}$与$y_{enemy}$、$x_{enemy}$与$y_{eat}$；

在处理每句话之前，都要检查这句话的真假：
有两种信息与”x与y是同类“矛盾：

1. $x_{self}$与$y_{eat}$在同一集合，说明y吃x；
2. $x_{eat}$与$y_{self}$在同一集合，说明x吃y；
   有两种信息与”x吃y矛盾“：
3. $x_{self}$与$y_{self}$在同一集合，说明x与y是同类；
4. $x_{self}$与$y_{eat}$在同一集合，说明y吃x；

这道题狗血问题挺多的，首先用cin、cout关流也会超时，然后不能写成多组样例输入（可能是scanf行为的问题，没正经研究过C）
然后就很正常了，ICPC之路任重道远啊！！！

const int MAX = 50005;

int father[3 * MAX], n, k;

void init(int num)
{
    for (int i = 0; i <= 3 * num; ++i)
        father[i] = i;
}

int getFather(int son)
{
    if (father[son] == son) return son;
    else return father[son] = getFather(father[son]);
}

void merge(int x, int y)
{
    x = getFather(x);
    y = getFather(y);
    father[x] = y;
}

int main()
{
    scanf("%d%d", &n, &k);

    init(n);
    int d, x, y, ans = 0;

    for (int i = 0; i < k; ++i)
    {
        scanf("%d %d %d", &d, &x, &y);

        if (x > n || y > n)
        {
            ans++;
            continue;
        }

        int x_self = x;
        int y_self = y;
        int x_eat = x + n;
        int y_eat = y + n;
        int x_enemy = x + 2 * n;
        int y_enemy = y + 2 * n;

        if (d == 1) // x与y是同类
        {
            if (getFather(x_eat) == getFather(y_self) || getFather(x_self) == getFather(y_eat))
                ans++;
            else
            {
                merge(x_self, y_self);
                merge(x_eat, y_eat);
                merge(x_enemy, y_enemy);
            }
        }
        else // x吃y
        {
            if (getFather(x_self) == getFather(y_self) || getFather(x_self) == getFather(y_eat))
                ans++;
            else
            {
                merge(x_self, y_enemy);
                merge(x_eat, y_self);
                merge(x_enemy, y_eat);
            }
        }
    }

    printf("%d\n", ans);
}

---

树状数组（Binary Indexed Trees）

若一个正整数$x$的二进制表示为$a_{k-1}{a}_{k-2}...a_2{a}_1{a}_0$，其中等于一的位是$a_{i_1},a_{i_2},a_{i_3},...,a_{i_m}$，则正整数$x$可以被二进制分解为：

$$x=2^{i_1}+2^{i_2}+2^{i_3}+...+2^{i_m}$$

不妨设$i_1>i_2>,,,>i_m$，进一步地，区间$[1,x]$可以分成$O(\log x)$个小区间：

1. 长度为$2^{i_1}$的小区间$[1,2^{i_1}]$
2. 长度为$2^{i_2}$的小区间$[2^{i_1}+1,2^{i_1}+2^{i_2}]$
3. 长度为$2^{i_3}$的小区间$[2^{i_1}+2^{i_2}+1,2^{i_1}+2^{i_2}+2^{i_3}]$
   …

这些小区间共同的特点是：若区间结尾为$R$，则区间长度就等于$lowbit(R)$。例如：

$$x=7=2^2+2^1+2^0$$

区间可以分为$[1,4]、[5,6]、[7,7]$三个小区间，长度分别是$lowbit(4)=4、lowbit(6)=2、lowbit(7)=1$。

下面这段代码可以计算出区间$[1,x]$分成的$O(\log x)$个小区间：

while (x > 0)
{
    printf("[%d, %d]\n", x - (x & -x), x);
    x -= (x & -x);
}

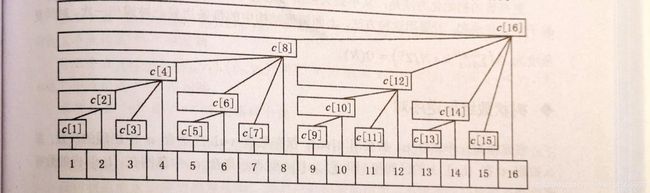
树状数组(Binary Indexed Trees)就是一种建立在上述思想上的数据结构，其基本用途是维护区间的前缀和。

对于给定的序列$a[]$我们建立一个数组$c[]$，其中$c[x]$保存$a[x-lowbit(x)+1]$到$a[x]$中所有数的和。

树状数组支持的基本操作有两个，第一个操作是查询前缀和，即$a[1]$到$a[x]$的和。按照我们刚才提出的方法，应该求出$x$的二进制表示中每一个等于$1$的位，把$[1,x]$分成$O(\log x)$个小区间，而每一个小区间的区间和都已经保存在数组$c[]$中，所以，将上面的代码改写即可已在$O(logx)$的时间内查询前缀和：

int query(int index)
{
    int ans = 0;
    for ( ; x > 0; x -= (x & -x))
        ans += c[x];
    return ans;
}

例如，对于上面那一张插图，计算${\sum }_{i=1}^{6}a[i]$，答案首先加上$c[6]$，然后因为$6$的二进制表示为$110$，减去$lowbit(6)$为$4$，此时答案再加上$c[4]$，最后$4-lowbit(4)=0$，循环终止，返回答案。

树状数组支持的第二个基本操作是单点增加，意思是给原始序列中一个数$a[x]$加上$y$，同时正确维护序列的前缀和。根据上面给出的树形结构和它的性质，只有节点$c[x]$及其所有祖先节点保存的“区间和”包含$c[x]$，而任意一个节点的祖先节点至多只有$\log N$个，逐一对其进行更新即可。下面的代码在$O(\log N)$的时间内进行单点增加操作。

void modify(int index, int delta)
{
    for ( ; index <= N; index += (index & -index))
        c[x] += delta;
}

在执行所有的操作之前，我们需要对树状数组进行初始化，为了简便，比较一般的初始化方法是：直接建立一个全为0的数组，然后对每一个位置执行修改操作，时间复杂度为$O(N\log N)$。通常采用这种初始化方法就已经足够。

更高效的初始化方法是：从小到大一次考虑每一个节点$x$，借助$lowbit$运算扫描它的子节点并求和。若采取这种方法，上面树形结构的每一条边只会被遍历一次，时间复杂度为$O(N)$。

树状数组模板

int arr[N]; // 原始数组
int tree[N]; // 树状数组

int lowbit(int x) // lowbit函数
{
    return x & -x;
}

int query(int index) // 查询前缀和
{
    int ans = 0;
    for ( ; index > 0; index -= lowbit(index))
        ans += tree[index];
    return ans;
}

void update(int index, int delta) // 单点更新
{
    for (; index <= N; index += lowbit(index))
        tree[index] += delta;
}

memset(tree, 0, sizeof(tree)); // 初始化
for (int i = 0; i <= N; ++i)
{
    update(i, arr[i]);
}

树状数组与逆序对

任意给定一个集合$a$，如果用$t[val]$保存数值$val$在$a$中出现的次数，那么$t$在$[l,r]$上的区间和（${\sum }_{i=l}^{r}t[i]$）就表示集合$a$中范围在$[l,r]$内的数有多少个。

我们可以在集合$a$的数值范围上建立一个树状数组，来维护$t$的前缀和，这样即使是在$a$中插入或者删除一个数，都可以进行高效的统计。

如果对于一个序列$a$，若$i<j$且$a[i]>a[j]$，就称$a[i]$与$a[j]$构成逆序对；按照上述思路，可以用以下方法利用树状数组求逆序对个数。

1. 在序列$a$的数值范围上建立树状数组，初始化为$0$；
2. 倒序扫描给定的序列$a$，对于每一个数$a[i]$：
   1. 在树状数组中查询前缀和$[1,a[i]-1]$，查询结果累加到$ans$中；
   2. 执行单点更新操作，将$a[i]$位置上的数加上$1$；表示$a[i]$又出现了一次；
3. $ans$即为所求逆序对个数；

代码：

int ans = 0;
for (int i = N; i > 0; --i)
{
    ans += query(a[i]);
    update(a[i], 1);
}
cout << ans << endl;

在这种解法中，因为倒序扫描，已经出现过的数就是$a[i]$后面的数，所以通过树状数组查询到的结果就是$a[i]$后面有几个数比它小，查询结果累加起来就是最后的答案。时间复杂度为$O((N+M)\log M)$，$M$为数值范围大小。

当数值范围较大时，当然可以先进行离散化，再用树状数组进行计算，不过因为离散化本身需要通过排序来实现，所以在这种情况下不如直接用归并排序来计算逆序对的个数了。

例题： Contest Hunter 4201 楼兰图腾

解法：

1. 倒序扫描序列$arr$，求出每一个$arr[i]$后面有几个数比它大，记为$Right[i]$。
2. 正序扫描序列$arr$，求出每一个$arr[i]$前面有几个数比它大，记为$Left[i]$。
3. ${\sum }_{i=1}^{N}Left[i]\ast Right[i]$就是$V$的个数。

“^”个数的求法同理。

看似很暴力的解法效率竟然还可以！10s的时限，以下代码272ms通过！
书本自带的标称看不懂?

using ll = long long;
constexpr ll MAX = 200000 + 5;

ll arr[MAX], tree[MAX], Left[MAX], Right[MAX], n;

ll lowbit(ll x)
{
    return x & -x;
}

ll query(ll index)
{
    ll ans = 0;
    for ( ; index > 0; index -= lowbit(index))
        ans += tree[index];
    return ans;
}

void update(ll index, ll delta)
{
    for (; index <= n; index += lowbit(index))
        tree[index] += delta;
}

int main()
{
    cin.sync_with_stdio(false);
    cin.tie(0);

    while (cin >> n)
    {
        for (ll i = 0; i < n; ++i)
            cin >> arr[i];

        memset(tree, 0, sizeof(tree));
        for (ll i = n - 1; i >= 0; --i)
        {
            Right[i] = query(arr[i] - 1); // 比arr[i]小的数的个数
            update(arr[i], 1);
        }

        memset(tree, 0, sizeof(tree));
        for (ll i = 0; i < n; ++i)
        {
            Left[i] = query(arr[i] - 1); // 比arr[i]小的数的个数
            update(arr[i], 1);
        }

        ll ans1 = 0;
        for (ll i = 0; i < n; ++i)
            ans1 += Left[i] * Right[i]; // 统计答案

        memset(tree, 0, sizeof(tree));
        for (ll i = n - 1; i >= 0; --i)
        {
            Right[i] = query(n) - query(arr[i]); // 比arr[i]大的数的个数
            update(arr[i], 1);
        }

        memset(tree, 0, sizeof(tree));
        for (ll i = 0; i < n; ++i)
        {
            Left[i] = query(n) - query(arr[i]); // 比arr[i]大的数的个数
            update(arr[i], 1);
        }

        ll ans2 = 0;
        for (ll i = 0; i < n; ++i)
            ans2 += Left[i] * Right[i]; // 统计答案

        cout << ans2 << " " << ans1 << endl;
    }
}

书本光盘带的标称

const int maxn=2000000;
int left[maxn],right[maxn],sum[maxn];
int i,j,n;
long long ans1,ans2;

void build(int l,int r,int c)
{
    int mid=(l+r)/2;
    left[c]=l;
    right[c]=r;
    sum[c]=0;
    if (l!=r)
    {
        build(l,mid,c*2);
        build(mid+1,r,c*2+1);
    }
}

void insert(int x,int c)
{
    int mid=(left[c]+right[c])/2;
    if (left[c]==right[c])
    {
        sum[c]=1;
        return;
    }
    if (x<=mid) insert(x,c*2);
    if (x>=mid+1) insert(x,c*2+1);
    sum[c]=sum[c*2]+sum[c*2+1];
}

int answer(int l,int r,int c)
{
    if (l>r) return 0;
    int mid=(left[c]+right[c])/2;
    if ((l==left[c])&&(r==right[c]))
         return sum[c];
    if (r<=mid) return answer(l,r,c*2);
    if (l>=mid+1) return answer(l,r,c*2+1);
    return answer(l,mid,c*2)+answer(mid+1,r,c*2+1);
}

int main()
{
    scanf("%d",&n);
    build(1,n,1);
    for (i=1;i<=n;i++)
    {
        int y;
        scanf("%d",&y);
        insert(y,1);
        ans1+=(long long)answer(y+1,n,1)*(n-y-answer(y+1,n,1));
        ans2+=(long long)answer(1,y-1,1)*(y-1-answer(1,y-1,1));
    }
    printf("%lld %lld\n",ans1,ans2);
    return 0;
}

树状数组的扩展应用

给出如下问题：

给定长度为$N(N\le 10^5)$，的数列$A$，然后输入$Q(Q\le 10^5)$行操作指令。
第一种指令形如“C l r d”，表示把数列中第l~r个数都增加d。
第二种指令形如“Q x”，表示询问数列中第x个数的数值。

本题的指令有“区间增加”和“单点查询”，而树状数组维护的是“前缀和”，仅支持“单点修改”，需要作出一些转化来应对这个问题。

建立一个新数组$b[]$，初始值全部设为零，对于每条指令“C l r d”，我们把它转化成以下两条指令：

1. $b[l]=b[l]+d$
2. $b[r+1]=b[r+1]-d$

在执行过上面两条指令后，我们来考虑一下数组$b[]$的前缀和（${\sum }_{i=1}^{x}b[i]$）的情况：

1. 对于$1\le x<l$，前缀和不变；
2. 对于$l\le x\le r$，前缀和增加了$d$；
3. 对于$r<x\le N$，前缀和不变；

可以发现，经过这一套骚操作，数组$b[]$的前缀和就反映了指令“C l r d”对$a[x]$的影响；

于是，我们可以利用树状数组来维护$b[]$的前缀和，因为各次操作之间具有可累加性，所以查询数组$b[]$的前缀和${\sum }_{i=1}^{x}b[i]$，就可以知道目前为止所有“C l r d”对$a[x]$增加的总数值，再加上$a[x]$本身的值，就是“Q x”操作的结果。

例题： POJ 3468 A Simple Problem with Integers

题意：

给定长度为$N(N\le 10^5)$，的数列$A$，然后输入$Q(Q\le 10^5)$行操作指令。
第一种指令形如“C l r d”，表示把数列中第l~r个数都增加d。
第二种指令形如“Q l r”，表示询问数列中第l~r个数的和。

前面我们已经讨论过，数组$b[]$的前缀和${\sum }_{i=1}^{x}b[i]$就是经过“C l r d”后$a[x]$增加的值，那么序列$a[]$的前缀和${\sum }_{i=1}^x$就是：

$$\sum _{i=1}^x\sum _{j=1}^{i}b[j]$$

上式可以改写为：（推导略……）

$$\sum _{i=1}^x\sum _{j=1}^{i}b[j]=\sum _{i=1}^x(x-i+1)\ast b[i]=(x+1)\sum _{i=1}^{x}b[i]-\sum _{i=1}^{x}i\ast b[i]$$

于是乎，对于这道题，就可以使用两个树状数组来维护；

具体来说，建立两个树状数组$c_0$和$c_1$，初始值全部设为0，对于每条指令“C l r d”，执行以下四个操作：

1. 在树状数组$c_0$中，把位置$l$上的数加上$d$；
2. 在树状数组$c_0$中，把位置$r+1$上的数减去$d$；
3. 在树状数组$c_1$中，把位置$l$上的数加上$l\ast d$；
4. 在树状数组$c_1$中，把位置$r+1$上的数减去$(r+1)\ast d$；

除此之外，我们建立一个数组$sum[]$，储存数组$a[]$原始的前缀和，对于每一条指令“Q r l”，计算：

$$(sum[r]+(r+1)\ast query(c_0,r)-query(c_1,r))-(sum[l-1]+l\ast query(c_0,l-1)-query(c_1,l-1))$$

自己写的代码：（3219ms）

typedef long long ll;
const ll MAX = 100000 + 5;

ll c0[MAX], c1[MAX], sum[MAX], n, q;

ll lowbit(ll x)
{
    return x & -x;
}

ll query(ll c[], ll index)
{
    ll ans = 0;
    for ( ; index > 0; index -= lowbit(index))
        ans += c[index];
    return ans;
}

void update(ll c[], ll index, ll delta)
{
    for ( ; index <= n; index += lowbit(index))
        c[index] += delta;
}

int main()
{
    cin.sync_with_stdio(false);
    cin.tie(0);

    while (cin >> n >> q)
    {
        memset(sum, 0, sizeof(sum));
        memset(c0, 0, sizeof(c0));
        memset(c1, 0, sizeof(c1));

        for (int i = 1; i <= n; ++i)
        {
            ll t;
            cin >> t;
            sum[i] = sum[i - 1] + t;
        }

        char cmd;
        ll l, r, d;
        while (q--)
        {
            cin >> cmd;

            if (cmd == 'C')
            {
                cin >> l >> r >> d;

                update(c0, l, d);
                update(c0, r + 1, -d);

                update(c1, l, l * d);
                update(c1, r + 1, -(r + 1) * d);
            }
            else
            {
                cin >> l >> r;

                ll ans = 0;

                ans += sum[r];
                ans += (r + 1) * query(c0, r);
                ans -= query(c1, r);

                ans -= sum[l - 1];
                ans -= l * query(c0, l - 1);
                ans += query(c1, l - 1);

                cout << ans << endl;
            }
        }
    }
}

书本标称1907ms（赌五毛是输入输出的锅(╯‵□′)╯︵┻━┻）

值得指出的是，为什么要把${\sum }_{i=1}^x(x-i+1)\ast b[i]$变成$(x+1)\ast {\sum }_{i=1}^{x}b[i]-{\sum }_{i=1}^{x}i\ast b[i]$进行统计呢？？？仔细观察该式的定义，这里的变量$x$是关于前缀和${\sum }_{i=1}^{x}a[i]$这个询问的变量，而$i$是每一次修改时影响的对象。

对于前者来说，求和式中的每一项同时包含$x$和$i$，在修改时无法确定$(x-i+1)$的值，只能维护$b[i]$的前缀和，在询问时需要面对一个“系数为等差数列”的求和式，计算起来非常困难。

对于后者来说，求和式中的每一项都只与$i$有关。它通过一次容斥，把$(x+1)$提取为常量，使得$b[i]$的前缀和与$i\ast b[i]$的前缀和可以分别由树状数组进行维护，这种分离包含有多个变量的项，使公式中不同的变量之间相互独立的思想非常重要，我们在下一章讨论动态规划的优化策略时会多次用到。

例题： POJ 2182 Lost Cows

有$n$头奶牛（$n\le 10^5$），已知它们的身高为$[1,n]$且各不相同，但不知道每一头奶牛的具体身高。
现在这$n$头奶牛站成一排，已知第$i$头奶牛前面有$A_i$头奶牛比它低，求每一头奶牛的身高。

如果最后一头奶牛前面有$A_n$头奶牛比它高，那么显然它的身高是$H_n=A_n+1$;
如果倒数第二头奶牛前面有$A_{n-1}$头奶牛比它身高高，那么：

1. 如果$A_{n-1}<A_n$，则它的身高$H_{n-1}=A_{n-1}+1$；
2. 如果$A_{n-1}\ge A_n$，则它的身高$H_{n-1}=A_{n-1}+2$；

以此类推，如果第$k$头奶牛前面有$A_k$头奶牛身高比它高，那么它的身高$H_k$是数值$[1,n]$中第$A_k+1$小的没有在$\{H_{k+1},H_{k+2},...,H_n\}$中出现过的数。

具体来说，我们建立一个长度为$n$的$01$序列$b[]$，初始值全部设为$1$。然后，倒序扫描每一个$A_i$并执行以下两个操作：

1. 查询序列$b$中第$A_i+1$个$1$在什么位置，这个位置号就是第$i$头奶牛的身高$H_i$。
2. 把$b[H_i]$置为零。

也就是说，我们需要维护一个01序列，支持查询第$k$个1的位置，以及修改序列中的一个数值。

方法一：树状数组 + 二分，单次操作$O({\log }^{2}n)$
方法二：树状数组 + 倍增，单次操作$O(\log n)$

自己的代码，树状数组 + 二分，110ms；书本标称一样的方法63ms，输入输出。。。

const int MAX = 8000 + 5;

int tree[MAX], A[MAX], H[MAX], n;

int lowbit(int x)
{
    return x & -x;
}

int query(int index)
{
    int ans = 0;
    for ( ; index > 0; index -= lowbit(index))
        ans += tree[index];
    return ans;
}

void update(int index, int delta)
{
    for ( ; index <= n; index += lowbit(index))
        tree[index] += delta;
}

int binarySearch(int index)
{
    int left = 1, right = n, mid;

    while (left < right)
    {
        mid = (left + right) >> 1;

        int num = query(mid);

        if (num >= index)
            right = mid;
        else
            left = mid + 1;
    }

    return left;
}

int main()
{
    cin.sync_with_stdio(false);
    cin.tie(0);

    while (cin >> n)
    {
        memset(A, 0, sizeof(A));
        memset(H, 0, sizeof(H));
        memset(tree, 0, sizeof(tree));

        for (int i = 1; i <= n; ++i)
            update(i, 1);

        for (int i = 2; i <= n; ++i)
            cin >> A[i];

        for (int i = n; i > 0; --i)
        {
            H[i] = binarySearch(A[i] + 1);
            update(H[i], -1);
        }

        for (int i = 1; i <= n; ++i)
            cout << H[i] << endl;
    }
}

补充：二维树状数组

no bb just watch the code!

int tree[MAX_ROWS + 1][MAX_COLS + 1];

int lowbit(int x) 
{
    return x & -x;
}

int query(int rows, int cols)
{
    int ans = 0;
    for (int i = rows; i > 0; i -= lowbit(i))
    {
        for (int j = cols; j > 0; j -= lowbit(j))
        {
            ans += tree[i][j];
        }
    }
    return ans;
}

void update(int rows, int cols, int delta)
{
    for (int i = rows; i <= MAX_ROWS; i += lowbit(i))
    {
        for (int j = cols; j <= MAX_COLS; j += lowbit(j))
        {
            tree[i][j] += delta;
        }
    }
}

---

线段树（Segment Tree）

线段树是一种基于分治思想的二叉树结构，用于在区间上进行信息统计。与按照二进制位 进行区间划分的树状数组相比，是一种更加通用的数据结构：

1. 线段树的每一个节点都代表一个区间；
2. 线段树具有唯一的根节点，代表的区间是整个统计范围；
3. 线段树的每一个叶节点都代表一个长度为$1$的元区间$[x,x]$；
4. 对于每个内部节点$[l,r]$，它的左子节点是$[l,mid]$，右子节点是$[mid+1,r]$，其中$mid=(l+r)>>1$（向下取整）

可以发现，出去树的最后一层，整棵线段树一定是一棵完全二叉树，树的深度为$O(\log N)$。因此，我们可以按照与二叉堆类似的父子二倍结点编号法：

1. 根节点的编号为1
2. 编号为$x$的节点的左子节点编号为$x\ast 2$，右子节点的编号为$2\ast x+1$。

这样一来，就可以用结构体数组来保存线段树；
在理想情况下，$N$个节点的满二叉树有$N+N/2+N/4+...+2+1=2N-1$个节点，因为在上述储存方式下，还有最后一层产生了空余，所以保存线段树的数组长度要不小于$4N$才能保证不会越界。

线段树的建树

线段树的基本用途是对序列进行维护，支持查询与修改指令，给定一个长度为$N$的序列$A$，我们可以在区间$[1,N]$上建立一棵线段树，每个叶节点$[i,i]$保存$A[i]$的值，线段树的二叉树结构可以很方便的从下往上传递信息。

以区间最大值的问题为例，记$data(l,r)$等于$ma{x}_{l\le i\le r}\{A[i]\}$，显然$data(l,r)=max(data(l,mid),data(mid+1,r))$。

以下代码建立了一棵线段树并保存相应区间上的最大值：

int A[N];

struct SegmentTree
{
    int left;
    int right;
    int value;
} tree[4 * N];

void build(int index, int left, int right)
{
    tree[index].left = left;
    tree[index].right = right;

    if (left == right) 
    {
        tree[index].value = A[left]; // 叶节点
    }
    else 
    {
        int mid = (left + right) >> 2; // 向下取整
        build(2 * index, left, mid); // 左子树
        build(2 * index + 1, mid + 1, right); // 右子树
        tree[index].value = max(tree[2 * index].value, tree[2 * index + 1].value);
    }
}

build(1, 1, N); // 调用入口

线段树的单点修改

单点修改是一条形如“C x v”的指令，表示把$A[x]$的值修改为$v$。

在线段树中，根节点是执行各种指令的入口，我们需要从根节点出发，递归找到代表$[x,x]$的叶节点，然后从下往上更新$[x,x]$以及它所有祖先节点上保存的信息，时间复杂度为$O(\log N)$。

代码如下所示：

void change(int index, int pos, int newValue)
{
    if (tree[index].left == tree[index].right)
    {
        tree[index].value == newValue;
    }
    else 
    {
        int mid = (tree[index].left + tree[index].right) >> 1;
        
        if (pos <= mid)
            change(2 * index, pos, newValue); // 要更新的节点在左子树上
        else 
            change(2 * index + 1, pos, newValue); // 要更新的节点在右子树上

        tree[index].value = max(tree[2 * index].value, tree[2 * index + 1].value); // 从下往上更新信息
    }
}

线段树的区间查询

区间查询是一条形如“Q l r”的指令，例如查询区间$[l,r]$上的最大值。

我们只需要从根节点开始，递归执行以下过程：

1. 若$[l,r]$完全覆盖了当前节点代表的区间，则立即回溯，并且该节点的$value$值作为候选答案。
2. 若左子节点与$[l,r]$有重叠部分，则递归访问左子节点。
3. 若右子节点与$[l,r]$有重叠部分，则递归访问右子节点。

代码示例如下：

int query(int index, int from, int to) // 用from、to代替上文的l、r
{
    if (from <= tree[index].left && tree[index.right] <= to)
    {
        return tree[idnex].value;
    }
    else 
    {
        int mid = (tree[index].left + tree[index].right) >> 1;

        int ans = INT_MIN; // 找一个最小值出来作比较

        if (from <= mid)
            ans = max(ans, query(2 * index, from, to)); // 与左子树有重合
        if (mid + 1 <= to)
            ans = max(ans, query(2 * index + 1, from, to)) // 与右子树有重合

        return ans;    
    }
}

cout << query(1, from, to); // 调用入口

query(1, 2, 8)

该查询过程会把查询区间$[from,to]$在线段树上分成$O(\log N)$个节点，取它们的最大值作为答案。（时间效率如何证明略ε=ε=ε=(~￣▽￣)~，参考原书）。

在讨论区间修改之前，先来A几道题

例题： Contest Hunter 4301 Can you answer on these queries III

在线段树的每一个节点上，除了区间端点之外，再维护四个信息：区间和$sum$，区间最大连续子段和$value$，紧靠左端的最大连续子段和$lmax$，紧靠右端的最大连续子段和$rmax$。

线段树的整体框架不变，我们只需要完善在$build$和$change$函数中从下往上传递的信息：

$$tree[index].sum=tree[2\ast index].sum+tree[2\ast index+1].sum$$
$$tree[index].lmax=max(tree[2\ast index].lmax,tree[2\ast index].sum+tree[2\ast index+1].lmax)$$
$$tree[index].rmax=max(tree[2\ast index+1].rmax,tree[2\ast index+1].sum+tree[2\ast index].rmax)$$
$$tree[index].value=max(tree[2\ast index].value,tree[2\ast index+1].value,tree[2\ast index].rmax+tree[2\ast index+1].lmax)$$

自己的代码，注意各个函数中状态的更新：

using ll = long long;

constexpr ll MAX = 500000 + 5, inf = -0x3fffffff;

ll arr[MAX], n, m;

struct SegmentTree
{
    ll left, right, value, sum, lmax, rmax;
} tree[4 * MAX];

void init(SegmentTree& t, ll val)
{
    t.value = t.rmax = t.lmax = t.sum = val;
}

void pushDown(ll index)
{
    tree[index].sum = tree[2 * index].sum + tree[2 * index + 1].sum;

    tree[index].lmax = max(tree[2 * index].lmax, tree[2 * index].sum + tree[2 * index + 1].lmax);

    tree[index].rmax = max(tree[2 * index + 1].rmax, tree[2 * index + 1].sum + tree[2 * index].rmax);

    tree[index].value = max(max(tree[2 * index].value, tree[2 * index + 1].value), tree[2 * index].rmax + tree[2 * index + 1].lmax);
}

void build(ll index, ll left, ll right)
{
    tree[index].left = left;
    tree[index].right = right;

    if (left == right)
    {
        tree[index].value = arr[left];
        tree[index].lmax = arr[left];
        tree[index].rmax = arr[left];
        tree[index].sum = arr[left];
    }
    else
    {
        ll mid = (left + right) >> 1;

        build(2 * index, left, mid);
        build(2 * index + 1, mid + 1, right);

        pushDown(index);
    }
}

void change(ll index, ll pos, ll newValue)
{
    if (tree[index].left == tree[index].right)
    {
        tree[index].value = tree[index].sum = tree[index].lmax = tree[index].rmax = newValue;
    }
    else
    {
        ll mid = (tree[index].left + tree[index].right) >> 1;

        if (pos <= mid)
            change(2 * index, pos, newValue);
        else
            change(2 * index + 1, pos, newValue);

        pushDown(index);
    }
}

SegmentTree query(ll index, ll from, ll to) // 注意此题中查询函数的状态更新
{
    if (from <= tree[index].left && tree[index].right <= to)
    {
        return tree[index];
    }
    else
    {
        ll mid = (tree[index].left + tree[index].right) >> 1;

        SegmentTree a, b, c;

        init(a, inf);
        init(b, inf);
        c.sum = 0;

        if (from <= mid)
        {
            a = query(2 * index, from, to);
            c.sum += a.sum;
        }
        if (mid + 1 <= to)
        {
            b = query(2 * index + 1, from, to);
            c.sum += b.sum;
        }

        if (from > mid) // 考虑左子树未被访问
            c.lmax = b.lmax;
        else
            c.lmax = max(a.lmax, a.sum + b.lmax);

        if (to <= mid) // 考虑右子树未被访问
            c.rmax = a.rmax;
        else
            c.rmax = max(b.rmax, b.sum + a.rmax);

        c.value = max(max(a.value, b.value), a.rmax + b.lmax);

        return c;
    }
}

int main()
{
    cin.sync_with_stdio(false);
    cin.tie(0);

    while (cin >> n >> m)
    {
        for (ll i = 1; i <= n; ++i)
            cin >> arr[i];

        memset(tree, 0, sizeof(tree));
        build(1, 1, n);

        ll a, b, c;
        while (m--)
        {
            cin >> a >> b >> c;

            if (a == 1)
            {
                if (b > c) swap(b, c);

                cout << query(1, b, c).value << endl;
            }
            else
            {
                change(1, b, c);
            }
        }
    }
}

例题： Contest Hunter 4302 Interval GCD

给定一个长度为$N$的数列$A$，以及$M$条指令，（$N\le 10^5,M\le 10^5$），每条指令可能是以下两种之一：

1. “C l r d”，表示把$A[l],A[l+1],...,A[r]$都加上$d$；
2. “Q l r”，表示询问$A[l],A[l+1],...,A[r]$的最大公约数；

对于每一个询问，给出一个整数表示答案。

因为$gcd(x,y)=gcd(x,y-x),gcd(x,y,z)=gcd(x,y-x,z-y)...$，且该性质对任意多个整数都成立，我们可以构造一个长度为$N$的新数列$B$，其中$B[i]=A[i]-A[i-1]$，$B[1]$可以为任意值，称数列$B$为数列$A$的差分序列，用线段树维护其最大公约数。

这样一来，对于每次“Q l r”，只要求出$gcd(a[l],query(1,l+1,r))$即可。

在指令“C l r d”下，只有$B[l]$增加了d，$B[r]$减小了d，所以只需要两次单点修改。

一个线段树加一个树状数组即可。

代码写的比较乱:

using ll = long long;

constexpr ll MAX = 500000 + 5;

ll arr[MAX], diff[MAX], bin[MAX], n, m;

struct SegmentTree
{
    ll left, right, value;
} tree[4 * MAX];

ll gcd(ll a, ll b)
{
    if (b == 0) return a;
    else return gcd(b, a % b);
}

void build(ll index, ll left, ll right) // 线段树建树
{
    tree[index].left = left;
    tree[index].right = right;

    if (left == right)
    {
        tree[index].value = diff[left];
    }
    else
    {
        ll mid = (left + right) >> 1;

        build(2 * index, left, mid);
        build(2 * index + 1, mid + 1, right);

        tree[index].value = gcd(tree[2 * index].value, tree[2 * index + 1].value);
    }
}

void change(ll index, ll pos, ll delta) // 线段树单点修改
{
    if (tree[index].left == tree[index].right)
    {
        tree[index].value += delta;
    }
    else
    {
        ll mid = (tree[index].left + tree[index].right) >> 1;

        if (pos <= mid)
            change(2 * index, pos, delta);
        else
            change(2 * index + 1, pos, delta);

        tree[index].value = gcd(tree[2 * index].value, tree[2 * index + 1].value);
    }
}

ll query(ll index, ll from, ll to) // 线段树区间查询
{
    if (from <= tree[index].left && tree[index].right <= to)
        return abs(tree[index].value);

    ll mid = (tree[index].left + tree[index].right) >> 1;

    ll ans = 0;

    if (from <= mid)
        ans = gcd(ans, query(2 * index, from, to));
    if (to >= mid + 1)
        ans = gcd(ans, query(2 * index + 1, from, to));

    return abs(ans);
}

ll bin_query(ll index) // 树状数组查询前缀和
{
    ll ans = 0;
    for ( ; index > 0; index -= (index & -index))
        ans += bin[index];
    return ans;
}

void bin_add(ll index, ll delta) // 树状数组单点修改
{
    for ( ; index <= n; index += (index & -index))
        bin[index] += delta;
}

int main()
{
    cin.sync_with_stdio(false);
    cin.tie(0);

    while (cin >> n >> m)
    {
        for (ll i = 1; i <= n; ++i)
        {
            cin >> arr[i];
            diff[i] = arr[i] - arr[i - 1];
        }

        build(1, 1, n);

        char cmd;
        ll x, y, z;
        while (m--)
        {
            cin >> cmd;

            if (cmd == 'Q')
            {
                cin >> x >> y;

                ll al = arr[x] + bin_query(x);
                ll val = query(1, x + 1, y);

                cout << gcd(al, val) << endl;
            }
            else
            {
                cin >> x >> y >> z;

                change(1, x, z);
                change(1, y + 1, -z);

                bin_add(x, z); // 树状数组维护arr数组中每一个位置增加的情况
                bin_add(y + 1, -z);
            }
        }
    }
}

延迟标记（区间修改）

在线段树的“区间查询”指令中，每当遇到被询问区间$[l,r]$完全覆盖的节点时，可以立即把该节点上储存的信息作为候选答案返回.我们已经证明，被询问区间$[l,r]$会被线段树分成$O(\log N)$个小区间（节点），从而在$O(\log N)$的时间内求出答案。

不过，在“区间修改指令”中，如果某个节点被修改区间$[l,r]$完全覆盖，那么以该节点为根的整棵子树的所有节点储存的信息都会发生变化，若逐一进行更新，将使得一次区间修改的指令的时间按复杂度增加到$O(N)$，这是无法接受的。

试想，如果我们在一次区间修改指令中发现节点$p$代表的区间$[p_l,p_r]$被修改区间$[l,r]$完全覆盖，并且我们逐一更新了子树$p$中的所有节点，但在之后的查询指令中却根本没有用到$[l,r]$的子区间作为候选答案，那么更新整棵子树都是徒劳的。

换言之，在执行区间修改指令时，同样可以在$l\le p_l\le p_r\le r$的情况下立即返回，只不过在回溯之前向节点$p$增加一个标记，标识该节点“曾经被修改”，但其子节点未被更新。

如果在后续的指令中，需要从节点$p$向下递归，我们再检查节点$p$是否被标记，若有标记，就根据节点$p$储存的信息更新其两个子节点，同时为这两个子节点增加标记，最后清除$p$的标记。

也就是说，除了在修改指令中直接划分成的$O(\log N)$个节点之外，对任意节点的修改都延迟到“在后续的操作中递归进入它的父节点时”再执行。这样一来，每条查询或修改指令的时间复杂度都降低到了$O(\log N)$。这些标记被称为“延迟标记”，延迟标记提供了线段树中从上往下传递信息的方式。这种延迟也是设计算法与解决问题的一个重要思路。

例题： POJ 3468 A Simple Problem with Integers

自己写的代码，3907ms，比树状数组稍慢一点→_→

typedef long long ll;

const ll MAX = 100000 + 10;

struct SegmentTree
{
    ll left, right, sum, add;
} tree[4 * MAX];

ll arr[MAX], n, m;

void build(ll index, ll left, ll right)
{
    tree[index].left = left;
    tree[index].right = right;

    if (left == right)
    {
        tree[index].sum = arr[left];
    }
    else
    {
        ll mid = (left + right) >> 1;

        build(2 * index, left, mid);
        build(2 * index + 1, mid + 1, right);

        tree[index].sum = tree[2 * index].sum + tree[2 * index + 1].sum;
    }
}

void spread(ll index)
{
    if (tree[index].add != 0)
    {
        tree[2 * index].sum += tree[index].add * (tree[2 * index].right - tree[2 * index].left + 1); // 更新左子节点

        tree[2 * index + 1].sum += tree[index].add * (tree[2 * index + 1].right - tree[2 * index + 1].left + 1); // 更新右子节点

        tree[2 * index].add += tree[index].add; // 给左子节点打延迟标记

        tree[2 * index + 1].add += tree[index].add; // 给右子节点打延迟标记

        tree[index].add = 0; // 消除根节点的延迟标记
    }
}

void change(ll index, ll from, ll to, ll delta)
{
    if (from <= tree[index].left && tree[index].right <= to)
    {
        tree[index].sum += delta * (tree[index].right - tree[index].left + 1); // 更新节点信息

        tree[index].add += delta;
    }
    else
    {
        spread(index); // 向下传递延迟标记

        ll mid = (tree[index].left + tree[index].right) >> 1;

        if (from <= mid)
            change(2 * index, from, to, delta);
        if (mid + 1 <= to)
            change(2 * index + 1, from, to, delta);

        tree[index].sum = tree[2 * index].sum + tree[2 * index + 1].sum;
    }
}

ll query(ll index, ll from, ll to)
{
    if (from <= tree[index].left && tree[index].right <= to)
        return tree[index].sum;
    else
    {
        spread(index); // 向下传递延迟标记

        ll mid = (tree[index].left + tree[index].right) >> 1, ans = 0;

        if (from <= mid)
            ans += query(2 * index, from, to);
        if (to >= mid + 1)
            ans += query(2 * index + 1, from, to);

        return ans;
    }
}

int main()
{
    cin.sync_with_stdio(false);
    cin.tie(0);

    while (cin >> n >> m)
    {
        // memset(tree, 0, sizeof(tree)); // 没有多组样例输入→_→
        
        for (ll i = 1; i <= n; ++i)
            cin >> arr[i];
        
        build(1, 1, n);

        char cmd;
        ll l, r, d;
        while (m--)
        {
            cin >> cmd;
            
            if (cmd == 'C')
            {
                cin >> l >> r >> d;
                change(1, l, r, d);
            }
            else
            {
                cin >> l >> r;
                cout << query(1, l, r) << endl;
            }
        }
    }
}

扫描线

例题： POJ 1151 Atlantis

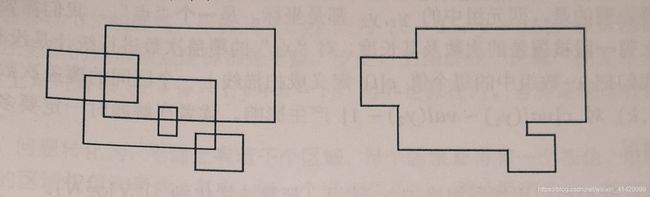
给定平面直角坐标系中的$N$个矩形，并求它们的面积并，即这些矩形的并集在坐标系中覆盖的总面积。

试想，如果我们用一条竖直直线从左到右扫过整个坐标系，那么直线上被并集图形覆盖的长度只会在每个图形的左右边界处发生变化。

换言之，整个并集图形可以被分成$2\ast N$段，每一段在直线上覆盖的长度（记为$L$）是固定的，因此该段的面积就是$L\ast$该段的宽度，各段面积之和即为所求答案。这跟直线就被称为扫描线，这种解题思路就被称为扫描线法。

具体来说，我们可以取出$N$个矩形的左右边界。若一个矩形的两个顶点为$(x_1,y_1),(x_2,y_2)$，其中$x_1<x_2,y_1<y_2$，则左边界记为四元组$(x_1,y_1,y_2,1)$，右边界记为四元组$(x_2,y_1,y_2,-1)$，把这$2N$个四元组按照横坐标递增的顺序排序。

注意到本题中纵坐标范围较大且不一定是整数，我们需要先对纵坐标进行离散化。设$val(y)$表示$y$被离散化后映射到的数值，$raw(i)$表示整数$i$对应的原始$y$坐标值。

在离散化后，若有$M$个不同的$y$坐标值，分别对应$raw(1),raw(2),...,raw(M)$，则扫描线至多被分成$M-1$段，其中第$i$段的区间为$[raw(i),raw(i+1)]$。

建立数组$c[]$，用$c[i]$记录扫描线上第$i$段被覆盖的次数，初始值全为0。

逐一扫描排序后的$2N$个四元组，设当前的四元组为$(x,y_1,y_2,k)$，首先，我们把$c[val(y_1)],c[val(y_1)+1],...,c[val(y_2)-1]$这些值都加上$k$，相当于覆盖了$[y_1,y_2]$这个区间。

此时，如果下一个四元组的横坐标为$x_2$，则扫描线从$x$扫描到$x_2$的过程中，被覆盖的长度就固定为${\sum }_{c[i]>0}(raw(i+1)-raw(i))$，即数组$c[]$中至少被覆盖过一次的段的总长度。

于是，我们就在当前答案上累加$(x_2-x)\ast {\sum }_{c[i]>0}(raw(i+1)-raw(i))$。

对于每个四元组，采用朴素算法在数组$c[]$上进行修改与统计，可以在$O(N^2)$的时间内求出每个并集图形的面积。

感动，纯自己写的竟然一发过了/(ㄒoㄒ)/~~，忽略CE、PE→_→
79ms, as shown below:

const int MAX = 150;

struct element
{
    double x, y1, y2; // 四元组储存边的信息
    int k;
} edges[2 * MAX];

bool cmp(element e1, element e2) // POJ的C++98(* ￣︿￣)
{
    return e1.x < e2.x;
}

int n, m, cases = 1, c[2 * MAX];
double ys[2 * MAX]; // 纵坐标离散化

int val(double y) // 题解里的val操作
{
    return int(lower_bound(ys, ys + m, y) - ys);
}

double raw(int i) // 题解里的raw操作
{
    return ys[i];
}

int main()
{
    cin.sync_with_stdio(false);
    cin.tie(0);

    while (cin >> n && n > 0)
    {
        cout << "Test case #" << cases++ << endl;

        int index = 0;
        double x1, x2, y1, y2;
        for (int i = 0; i < n; ++i)
        {
            cin >> x1 >> y1 >> x2 >> y2;

            edges[index].x = x1; // 记录四元组
            edges[index].y1 = y1;
            edges[index].y2 = y2;
            edges[index].k = 1;
            ys[index] = y1;

            index++;

            edges[index].x = x2; // 记录四元组
            edges[index].y1 = y1;
            edges[index].y2 = y2;
            edges[index].k = -1;
            ys[index] = y2;

            index++;
        }

        double ans = 0; // 答案
        memset(c, 0, sizeof(c)); // 题解里的数组c[]，初始值设置为0
        sort(edges, edges + index, cmp); // 为四元组排序
        sort(ys, ys + index); // 离散化1
        m = int(unique(ys, ys + index) - ys); // 离散化2

        for (int i = 1; i < index; ++i)
        {
            int val_y1 = val(edges[i - 1].y1);
            int val_y2 = val(edges[i - 1].y2);
            int k = edges[i - 1].k;

            double delta_x = edges[i].x - edges[i - 1].x;

            for (int i = val_y1; i < val_y2; ++i) // 更新扫描线的覆盖情况
            {
                c[i] += k;
            }

            for (int j = 0; j < m - 1; ++j) // 计算答案
            {
                if (c[j] > 0)
                {
                    ans += delta_x * (raw(j + 1) - raw(j));
                }
            }
        }

        cout << "Total explored area: " << fixed << setprecision(2) << ans << endl << endl;
    }
}

懒得用树状数组或者线段树维护$c[]$了，虽然可以把算法优化到$O(N\log N)$。

例题： POJ 2482 Stars in Your Window

天空中有很多星星（看作平面直角坐标系），已知每颗星星的坐标和亮度（都是整数），求用宽为$w$，高为$h$的矩形（均为整数）能圈住的星星的亮度总和的最大值（矩形边界上的星星不算）。

因为矩形的大小固定，所以此矩形可以由它的任意一个顶点确定，我们可以考虑把矩形的右上顶点放在什么位置，圈住的星星亮度总和最大。

对于一个星星$(x,y,c)$，能将其圈住的矩形的右上顶点能摆放的位置也是一个矩形区域，这个矩形区域的左下顶点为$(x,y)$，右上顶点为$(x+w,y+h)$。为了避免歧义，以下用区域代指这个范围。

由于题目中说矩形边界上的星星不算，为了处理这种情况，不妨将所有星星向左、向下移动$0.5$个单位距离，即坐标从$(x,y)$变为$(x-0.5,y-0.5)$；在此基础上，不妨假设圈住星星的矩形的顶点坐标都是整数。于是，上文的“区域”的左下角可以看作$(x,y)$，右上角可以看作$(x+w-1,y+h-1)$，边界也算在内，可以证明这些假设不会影响答案。(￣▽￣)"

此时，问题转化为：平面上有若干个区域，每个区域都带有一个权值，求在哪个坐标上重叠的区域权值和最大。其中，每一个区域都是由一颗星星产生的，权值等于星星的亮度，把原问题矩形的右上角放在该区域中，就能圈住这颗星星。

在转化后的问题中，我们使用扫描线算法，取出每个区域的左右边界，保存成两个四元组：$(x,y,y+h-1,c)$和$(x+w,y,y+h-1,-c)$，把这些四元组按照横坐标从小到大排序。

同时，关于纵坐标建立一棵线段树，维护区间最大值，初始值全部设为0，我们可以认为线段树上的一个值$y$代表元区间$[y,y+1]$，而区间$[y,y+h-1]$可以表示为线段树中的$y,y+1,y+2,...,y+h-1$这几个值，这样一来，线段树维护的就是若干个数值构成的序列了。

逐一扫描每个四元组$(x,y_1,y_2,c)$，并在线段树中执行区间修改，把$[y_1,y_2]$中的每一个数都加上$c$，然后用根节点的值更新答案即可。

自己的代码，266ms→_→

typedef long long ll;

ll n, w, h, discrete[20005], m;

struct element // 为扫描线服务的四元组
{
    ll x, y1, y2, c;
} stars[20005];

bool cmp(element e1, element e2)
{
    return e1.x < e2.x;
}

struct SegmentTree
{
    ll value, left, right, add;
} tree[20005 * 4]; // 线段树统计区间最大值

void build(ll index, ll left, ll right) // 线段树建树，因为还没有开始扫描，所以add和value都设为0
{
    tree[index].left = left;
    tree[index].right = right;
    tree[index].add = tree[index].value = 0;

    if (left == right) return;

    ll mid = (left + right) >> 1;

    build(2 * index, left, mid);
    build(2 * index + 1, mid + 1, right);
}

void spread(ll index)
{
    if (tree[index].add != 0)
    {
        tree[2 * index].add += tree[index].add;
        tree[2 * index].value += tree[index].add;

        tree[2 * index + 1].add += tree[index].add;
        tree[2 * index + 1].value += tree[index].add;

        tree[index].add = 0;
    }
}

void change(ll index, ll from, ll to, ll delta) // 区间修改
{
    if (from <= tree[index].left && tree[index].right <= to)
    {
        tree[index].value += delta;
        tree[index].add += delta;
    }
    else
    {
        spread(index);

        ll mid = (tree[index].left + tree[index].right) >> 1;

        if (from <= mid)
            change(2 * index, from, to, delta);
        if (to > mid)
            change(2 * index + 1, from, to, delta);

        tree[index].value = max(tree[2 * index].value, tree[2 * index + 1].value);
    }
}

int main()
{
    cin.sync_with_stdio(false);
    cin.tie(0);

    while (cin >> n >> w >> h)
    {
        ll len = 0, x, y, c;
        for (ll i = 0; i < n; ++i)
        {
            cin >> x >> y >> c;

            stars[len].x = x;
            stars[len].y1 = y;
            stars[len].y2 = y + h - 1;
            stars[len].c = c;
            discrete[len] = y;

            len++;

            stars[len].x = x + w;
            stars[len].y1 = y;
            stars[len].y2 = y + h - 1;
            stars[len].c = -c;
            discrete[len] = y + h - 1;

            len++;
        }

        sort(stars, stars + len, cmp);
        sort(discrete, discrete + len); // 离散化
        m = ll(unique(discrete, discrete + len) - discrete);
        build(1, 1, m); // 这里len其实就是2 * n，m是离散化后储存纵坐标的数组的长度

        for (ll i = 0; i < len; ++i)
        {
            // 更改纵坐标为离散化之后的值
            stars[i].y1 = lower_bound(discrete, discrete + m, stars[i].y1) - discrete;
            stars[i].y2 = lower_bound(discrete, discrete + m, stars[i].y2) - discrete;
        }

        ll ans = 0;
        for (ll i = 0; i < len; ++i) // 线段树统计区间最大值，只有两颗星星的“区域”相交，“亮度”才会叠加到一起
        {
            change(1, stars[i].y1, stars[i].y2, stars[i].c);
            ans = max(ans, tree[1].value);
        }

        cout << ans << endl;
    }
}

---

分块

Page217 2019-1-13 有缘再会→_→