CenterNet(Objects as Points)学习笔记

论文: Objects as Points
Code: https://github.com/xingyizhou/CenterNet

CenterNer的提出

• 一般的detection方法将object识别成(无旋转的)矩形框。大部分成功的object检测器会枚举出很多object的位置和尺寸，对每一个候选框进行分类。这是浪费的、低效的。
• 常规方法中的后处理方法(nms等)是很难微分(differentiate)和训练的。

本文中采取了一种不同的方法，它把object建模成一个点–对应bounding box的中心点, 该方法基于中心点，称作CenterNet。相比于对应的基于bbouding box的检测器，CenterNet是端到端可微分的，更简洁的，更快的，而且更精确的。

确立了中心点后，一些其他的特征，比如物体的尺寸，3D里的orientation, dimension, depth等信息，姿势估计里的关键点等信息，都可以直接该中心点的图像特征回归得到。因此，在这种思路下，object detection就是一个标准的关键点估计问题：把图像送入一个全卷积网络，产生一张heatmap，这张heatmap里的peaks就是物体的中心，在每一个peak位置的图像特征用来预测objects的宽度和高度。在检测时，没有nms作为后处理，是一个单一的forward-pass过程。

CenterNet方法是通用的，只需少量工作就可以扩展到其他的问题，如3D的object detection, 多人的姿态估计。实验结果也证明了这一点。

CenterNet 有什么优点?

• 它不基于anchor，不需要很多人工设置的超参数(anchor的尺寸，anchor的正负overlap iou阈值)
• 它不需要nms操作，容易训练
• 输出的分辨率较大(output stride = 4), 传统的目标检测器一般为 output stride = 16, 因此它可以忽略了需要多个尺寸检测的需求
• 相比于CornerNet、ExtremeNet等free-anchor的方法，它不需要把预测的点进行group的过程，因此更快。

CenterNet介绍

$I\in R^{W\ast H\ast 3}$表示一张宽W、高H的输入图像。CenterNet的目标是产生一张关键点heatmap $\hat{Y}\in [0,1{]}^{\frac{W}{R}\ast \frac{H}{R}\ast C}$, $R$是输出的stride, C是关键点类别的数量， 在COCO的object detection里 $C$ = 80。$R$一般选用4。骨干网络论文中采取了stacked hourglass network, up-ResNet和deep layer aggregation(DLA).

整个网络的输出包含C + 4个通道，所有的这些输出共享相同的全卷积骨干网络。接下来介绍的loss函数里会详细说明为啥是+4通到

heatmap中的值只有0，1是如何实现的?从论文下面介绍来看，这里产生的heatmap的大小还是在0-1之间，表示置信度。之后再看一下源码，确认一下。

${\hat{Y}}_{x,y,c}=1$表示一个检测到的关键点， ${\hat{Y}}_{x,y,c}=0$表示是背景。

CenterNet的Loss函数

• 关键点的分类loss

  对于每一个关键点$p\in R^2$, 设它的类别是$c$, 我计算它的低分率表示$\tilde{p}=\lfloor \frac{p}{R}\rfloor$, 这样可以通过如下的高斯核得到一个ground truth的heatmap $Y\in [0,1{]}^{\frac{W}{R}\ast \frac{H}{R}\ast C}$
  $$Y_{xyc}=exp(-\frac{(x-{\tilde{p}}_x{)}^2+(y-{\tilde{p}}_y{)}^2}{2{\sigma }_p^2})$$
  如果某一类的两个Gaussians重叠了，则选择最大值。

  loss函数为惩罚削减的逐像素的逻辑回归的focal loss。

  $$L_k=\frac{-1}{N}{\Sigma }_{xyc}=\{\begin{array}{l}(1-{\hat{Y}}_{xyc}{)}^{\alpha }log({\hat{Y}}_{xyc}),Y_{xyc}=1\\ \\ (1-Y_{xyc}{)}^{\beta }({\hat{Y}}_{xyc}{)}^{\alpha }log(1-{\hat{Y}}_{xyc}),others\end{array}$$
  $\alpha$和$\beta$是focal loss中的超参数，这里设置为$\alpha =2$, $\beta =4$。 $N$是在图像$I$里的关键点的数量，选择N进行归一化。

• 偏移(offset) loss
  由于output stride的存在，也产生了离散化误差，$\frac{p}{R}-\tilde{p}=\frac{p}{R}-\lfloor \frac{p}{R}\rfloor$，所以在每个中心点处也预测偏移$\hat{O}\in R^{\frac{W}{R}\ast \frac{W}{R}\ast 2}$，所有的c个类别贡献偏移预测量。

  偏移loss采取的L1 loss,
  $$L_{off}=\frac{1}{N}{\Sigma }_p|{\hat{O}}_{\tilde{p}}-(\frac{p}{R}-\tilde{p})|$$

  偏移loss只计算在关键点位置$\tilde{p}$的误差，其它所有的位置都会被忽略掉。

• 尺寸loss(宽、高)

  $(x_1^{(k)},y_1^{(k)},x_2^{(k)},y_2^{(k)})$表示objcet的bounding box, 它的类别是$c_k$。
  我们使用$\hat{Y}$来预测中心点，除此之外，论文中还要对每一个object k进行回归尺寸$s_k=(x_2^{(k)}-x_1^{(k)},y_2^{(k)}-y_1^{(k)})$。

  为了减轻计算负担，论文中对所有的object类别采用单一的尺寸预测 $\hat{S}\in R^{\frac{W}{R}\ast \frac{H}{R}\ast 2}$, 尺寸loss也采用L1 loss,

  $$L_{size}=\frac{1}{N}{\Sigma }_{k=1}^N|{\hat{S}}_{pk}-s_k|$$

  这里没有对尺度(scale)进行归一化，而是直接使用了元素图像的坐标。

训练的总的loss为
$$L_{det}=L_k+{\lambda }_{size}{L}_{size}+{\lambda }_{off}{L}_{off}$$
其中,${\lambda }_{size}=0.1,{\lambda }_{off}=1$

CenterNet的预测

在预测时首先独立的在heatmaps提取每一个类别的peaks。作者把heatmap中大于等于8邻域的位置当做是peaks，并选取top 100。

CenterNet最终预测多少个检测框呢或者通过什么方式控制的呢?有待解决

${\hat{P}}_c$表示类别c的n个检测中心, $\hat{P}={({\hat{x}}_i,{\hat{y}}_i)}_{i=1}^n$, 每一个关键点位置的坐标都是整数$(x_i,y_i)$, ${\hat{Y}}_{x_i,y_i,c}$是它检测的置信度，从而可以产生一个bounding box:
$$({\hat{x}}_i+\delta {\hat{x}}_i-{\hat{w}}_i/2,{\hat{y}}_i+\delta {\hat{y}}_i-{\hat{h}}_i/2,{\hat{x}}_i+\delta {\hat{x}}_i+{\hat{w}}_i/2,{\hat{y}}_i+\delta {\hat{y}}_i+{\hat{h}}_i/2,)$$

其中 $(\delta {\hat{x}}_i,\delta y_i)={\hat{O}}_{{\hat{x}}_i,{\hat{y}}_i}$是偏移量， $({\hat{w}}_i,{\hat{h}}_i)={\hat{S}}_{{\hat{x}}_i,{\hat{y}}_i}$是尺寸预测。

Peak keypoint提取可以同可以通过 3 x 3 的 maxpooling操作实现。

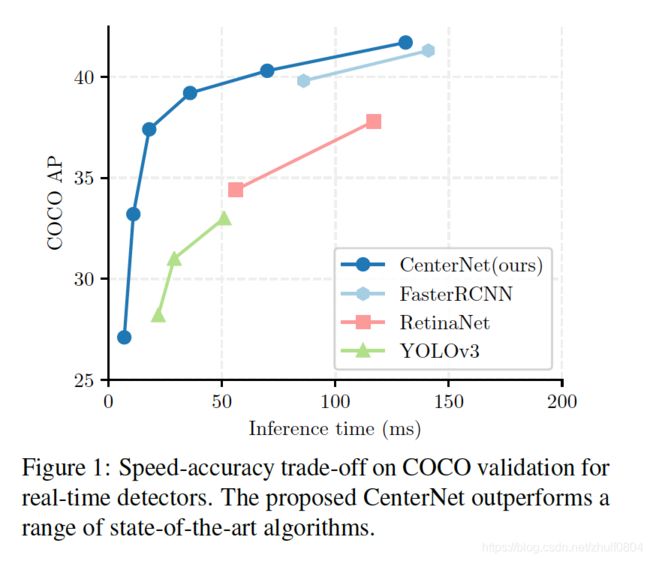
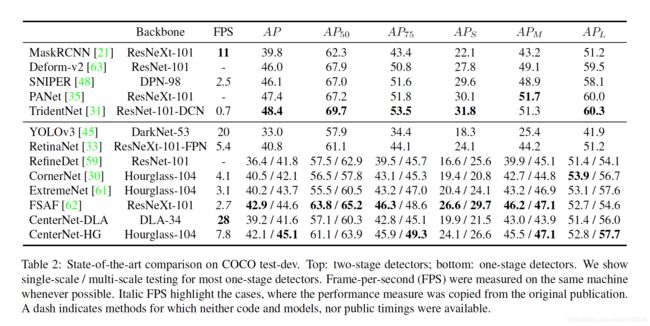
CenterNet的性能

速度和精度如下所示

CenterNet有什么缺点

• 当两个不同的object完美的对齐，可能具有相同的center，这个时候只能检测出来它们其中的一个object。

不确定的地方

• 每一个heatmap预测多少个object? 或者由heatmap怎么得到有效的center points?
• 当两个不同的object完美的对齐，可能具有相同的center，这个时候只能检测出来它们其中的一个object。 为什么只能检测出一个?