计算机图形学-3D观察与图像渲染流水线-投影全解析

本文目标：

1. 理清OpenGL在3D观察的整个流程。
2. 清楚各个专业术语的含义。
3. 对坐标系变换的数学有所掌握。

1 三维观察与观察流程

1.1 三维观察与照相观察的对比

• 三维观察过程与使用照相机拍摄照片类似

	对象	定位	场景范围	成像
照相	自然景物	设定相机位置、方向、相机的正向上方向	改变相机焦距大小	胶片
三维观察	三维虚拟场景	设置三维观察坐标系	选定观察体大小	观察平面

1.2 三维观察流水线(模型渲染管线)

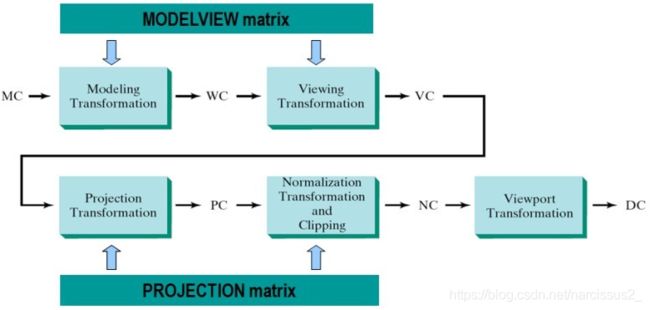
• 让我们先来弄清楚OpenGL中的渲染管线。管线是一个抽象的概念，之所以称之为管线是因为显卡在处理数据的时候是按照一个固定的顺序来的，而且严格按照这个顺序。就像水从一根管子的一端流到另一端，这个顺序是不能打破的。先来看看下面的图：

术语

• MC：模型坐标系
• Modelling transformation：模型变换
• WC：世界坐标系
• Viewing Transformation：视点变换
• VC：视界坐标系
• Projection Transformation:投影变换
• PC：投影坐标系
• Normalization Transformation and Clipping: 正则化变换和剪裁
• NC:正则化坐标
• View Transformation: 视窗转换
• DC: 设备坐标

图解

• 图中显示了OpenGL图形管线的主要部分，也是我们在进行图形编程的时候常常要用到的部分。
• 一个顶点数据从图的左上角(MC)进入管线，最后从图的右下角(DC)输出。
• MC是Model Coordinate的简写，表示模型坐标。DC是Device Coordinate的简写，表示设备坐标。当然DC有很多了，什么显示器，打印机等等。这里DC我们就理解成常说的屏幕坐标好了。MC是模型坐标，也说成本地坐标(相对于世界坐标)。MC要经过模型变换(Modeling Transformation)才变换到世界坐标（但是事实上这个转换时不存在的，只需要一个转换modelling转换到viewing 参考文章：https://blog.csdn.net/caoshangpa/article/details/80272903)

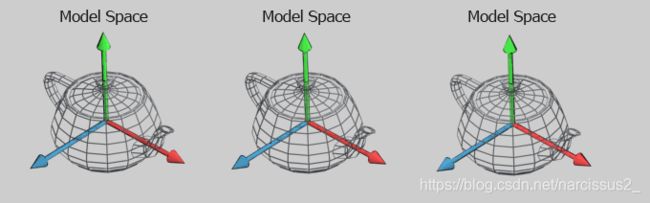
1.3 模型坐标系

• 这是模型在被应用任何变换之前的初始位置和方向所在的坐标系，也就是当前绘图坐标系。该坐标系不是固定的，且仅对该模型适用。
• 在默认情况下，该坐标系与世界坐标系重合。这里能用到的函数有glTranslatef()，glScalef(), glRotatef()，当用这些函数对当前绘图坐标系进行平移、伸缩、旋转变换之后， 世界坐标系和当前绘图坐标系不再重合。
• 改变以后，再用glVertex3f()等绘图函数绘图时，都是在**当前绘图坐标系进行绘图，所有的函数参数也都是相对当前绘图坐标系来讲的。**如图则是对物体进行变换后，模型坐标系与世界坐标系的相对位置。
• 模型坐标系也叫本地（局部）坐标系。

1.4 观察坐标系

• 模型变换：模型坐标系->世界坐标系
• 视变换：世界坐标系->观察坐标系
• 在OpenGL中，我们有GL_MODELVIEW矩阵，它代表着模型变换矩阵和视点变换矩阵的组合(Mview*Mmodel)，它可以直接使模型坐标系转换到世界坐标系。OpenGL中不存在单独的模型变换和视点变换，所以都使用GL_MODELVIEW矩阵使模型坐标系转换到观察坐标系。
  
• 默认情况下，眼坐标系和世界坐标系是重合的。使用函数gluLookAt()则可以指定眼睛(相机)的位置和眼睛看的方向，函数原型：

void gluLookAt(GLdouble eyex, GLdouble eyey, GLdouble eyez, 
                        GLdouble centerx, GLdouble centery, GLdouble centerz,
                        GLdouble upx, GLdouble upy, GLdouble upz)

函数参数中：
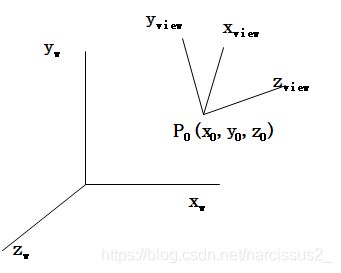
点(eyex, eyey, eyez)代表眼睛所在位置$p_0$；
点(centerx, centery,centerz)代表眼睛看向的位置；
向量(upx, upy, upz)代表视线向上方向，其中视点和参考点的连线与视线向上方向要保持垂直关系。（这个是view-up vector，为什么我们需要这个向量呢？因为我们可以歪着头看物品)

正着头看物品

歪着头看物品

定义观察坐标系过程

• 我们现在有“眼睛所在位置”，“眼睛看向的位置”，“视线向上方向”，于是：
• 我们可以获得VPN(view-plane normal vector)，是一个眼睛看向位置指向眼睛所在位置的向量(可以通过上面获取)，有了它就能定义$Z_{view}$方向，我们用N来表示它的单位向量。
• 用视线向上方向就可以直接获得$Y_{view}$方向，我们用V来表示它的单位向量。
• V和N的点积可以确定$x_{view}$，我们称为N，这样观察坐标系就确定完成了。
  
  
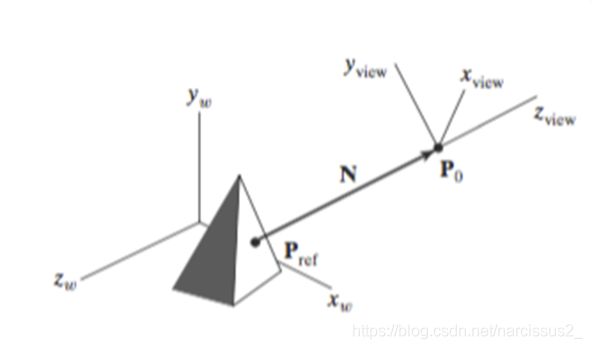
  注意：我们的观察物体在$Z_{view}$的负半轴上

定义观察平面

• 通常在观察坐标系中定义一个平面作为剪裁窗口所在的平面，即观察平面，它与$z_{view}$垂直，用一个标量设定观察平面在沿$z_{view}$轴方向的位置$z_{vp}$。
• 为从观察原点沿着观察方向到观察平面的距离，常被设置在负$z_{view}$方向。
• 观察平面的方向用平面法向量N来定义，并与$z_{view}$正轴同方向，观察平面总是与平面$x_{view}{y}_{view}$平行。
  （摘自三维观察:PPT)
  
  

向上向量(view-up vector)

• 我们发现，向上向量在输入gluLookAt的时候非常容易输入不精确（不和N严格垂直)，所以观察函数一般会自动调整向量V的方向。
• 通过将其投影到观察平面上得到与观察平面法向量垂直的向量作为V。

1.4.2 世界坐标系向相机坐标系的变换(难)

步骤1： 理解齐次坐标

https://blog.csdn.net/smilejiasmile/article/details/79606234

步骤2：让我们来举个2维的例子

我们来研究从MC到WC的坐标转换

**问题：**已知MC在WC的原点坐标为（4,3），在MC坐标上有点p(1,1)，求转换矩阵和这个点在WC的位置（用列向量表示)。

解：设点$p(x,y)$ 变换后的点为 $p^{\prime }(x^{\prime },y^{\prime })$，假设MC开口朝右（只是便于理解），那么我们的坐标系就不用通过旋转，那么有$$x^{\prime }=x+T_x,y^{\prime }=y+T_y$$
于是转换矩阵易得为$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& T_x\\ 0& 1& T_y\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}x+T_x\\ y+T_y\\ 1\end{array}\right]$$
带入$x=0,y=0,x^{\prime }=4,y^{\prime }=3$，则求出$T_x=4,T_y=3$。
此时再带入$x^{\prime }=1,y^{\prime }=1$求出$x=5,y=4$，这不是我们想要的结果，因为MC的开口朝左。此时我们需要让WC开口逆旋转90°。

用极坐标表示点P:

$$\{\begin{array}{r}x=r\cos \alpha \\ y=r\sin \alpha \end{array}$$

用极坐标表示点$p^{\prime }$

$$\{\begin{array}{r}{x}^{\prime }=r\cos (\alpha +\theta )=rcos\alpha cos\theta -rsina\alpha sin\theta \\ y^{\prime }=r\sin (\alpha +\theta )=rcos\alpha sin\theta +rsin\alpha cos\theta \end{array}$$
将上面的$x,y$带入下面的式子即可得到
$$\{\begin{array}{r}{x}^{\prime }=xcos\theta -ysin\theta \\ y^{\prime }=xsin\theta +ycos\theta \end{array}$$
于是即可推出
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]\cdot \left[\begin{array}{ccc}cos\theta & sin\theta & 0\\ -sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]$$
代入$\theta =90°$，则矩阵变成$$\left[\begin{array}{ccc}0& 1& 0\\ -1& 0& 0\\ 0& 0& 1\end{array}\right]$$
把(1,1)乘以旋转矩阵
$$\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]\cdot \left[\begin{array}{ccc}0& 1& 0\\ -1& 0& 0\\ 0& 0& 1\end{array}\right]=\left[\begin{array}{c}1\\ -1\\ 1\end{array}\right]$$
再把结果代入之前的平移矩阵：$$\left[\begin{array}{ccc}1& 0& 3\\ 0& 1& 4\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}1\\ -1\\ 1\end{array}\right]=\left[\begin{array}{c}4\\ 3\\ 1\end{array}\right]$$

根据二维方程，思考三维方程

推导思路是完全一样的，只是变成了从WC到MC。这个是平移矩阵，我们假定世界坐标系上有一点$p_0(x_0,y_0,z_0)$，那么我们发现转换矩阵的原点坐标变成了$p_0$坐标的相反数，这是因为相对$p_0$，世界坐标系的原点坐标就是这个位置。

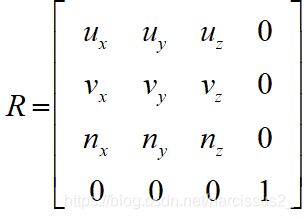
2. 投影变换

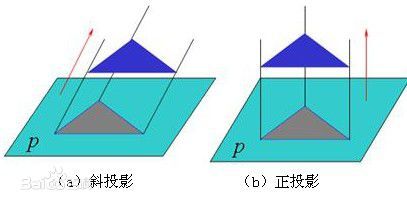
2.1 平行投影

• 转换为查看坐标后，对象描述将投影到视图平面。
• 在平行投影中，坐标位置沿着平行线转移到视图平面。
• 平行投影的特点，光源无限远，可以近似为平行光
• 两种方法获得平行投影
  • 沿垂直于平面的线投影（正投影）(parallel projections)
  • 以与视图倾斜的角度投影（斜投影）(Oblique parallel projections)
    
• P平面即为观察平面

正投影实例

斜投影实例

2.2 透视投影

• 在透视投影中，对象位置沿着会聚到视图平面后面点的线转换为投影坐标。
• 透视投影不保留对象的相对比例
• 场景视图更真实，因为投影显示中的远处对象的大小减小。

透视投影图片示例

2.2.1透视投影转换坐标

• 虚线表示空间位置$(x,y,z)$到$(x_{prp},y_{prp},z_{prp})$的投影参考点的投影路径。
• 投影线在视图平面与坐标位置$(x_p,y_p,z_{vp})$相交，其中$z_{vp}$是$z_{view}$轴上视图平面的某个选定位置（就说我们是通过确定z点来确定这些点的位置的)。
  
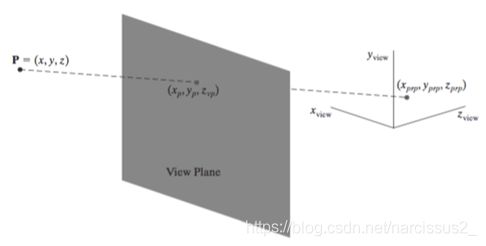
  描述沿该透视投影线的坐标位置的等式以参数形式表示为：
  
  由于z点已知，则可以用z代换u：
  
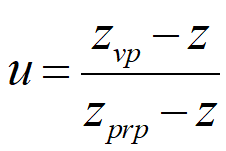
  通过代换，我们得到了新的方程：
  

2.2.2 相交点（灭点）（消失点）

• 一般灭点透视就分为三种，一点透视，二点透视和三点透视
  
• 使用透视映射将场景投影到视图平面上时，与视图平面平行的线将投影为平行线
• 但是，场景中与视平面不平行的任何平行线都会投影到会聚线中
• 消失点是指一组投影线看起来会聚的点 - 每组投影平行线都有一个单独的消失点
• 主要消失点是一组与一个物体的主轴平行的线
• 我们用投影平面的方向控制主要消失点的数量，因此透视投影被分类为一点，两点和三点投影
• 投影中的主要消失点的数量等于与视图平面相交的主轴的数量

2.3 正交投影

• 正交投影（或正交投影）是将对象描述沿与视图平面法向量n平行的直线转换为视图平面。
• 它最常用于生成对象的前视图、侧视图和俯视图。
• 物体的前、侧和后正交投影称为立面。
• 顶部正交投影称为平面图。
• 下面是两个正方体的示例

正视图(front evaluation view)

侧视图(side evaluation view)

俯视图(plan view)

2.4 正交投影视图体（orthogonal projection view volume）

• 我们这里强调一点，观察平面是一个无限平面，通常有uv轴构成，显然无限平面不可能容纳在有限平面内，因此定义了剪裁窗口。
  
• ※何为正交投影视图体积，其实就是正视图（前后两面）、俯视图（上下两面）、侧视图（左右两面），总计六面围城的长方体空间就称为正交投影视图体积。可以依靠上面的三视图想象。超出这个范围的外部场景将被剪切。
  

2.5 透视投影视图体（Perspective-projection view volume）

• 有正交投影视图体积就有透视投影视图体

• 透视投影视图体积通常被称为视觉金字塔(pyramid of vision)，因为它近似于我们眼睛的视锥或相机

• 通过添加垂直于$z_{view}$轴并平行于视图平面的近和远剪裁平面，我们切除无限透视投影视图体积的一部分，以形成截断的棱锥，或者称为棱台

• 我们从一个方向观察投影观察体
  
  

• 透视投影观察体完全可由视场角、裁剪窗口的横纵比及从投影参考点到近和远裁剪平面的距离来确定。裁剪窗口的左下角和右上角的坐标位置与棱台中心点及窗口的高、宽之间存在如下关系
  $$x_{wmin}=x_c-宽度/2，x_{wmax}=x_c+宽度/2，y_{wmin}=y_c-高度/2，y_{wmax}=y_c+高度/2$$

投影视图的规范化变换

• 透视投影观察体中透视投影变换，会将棱台内部的坐标位置，映射到矩形平行管道的正交投影坐标。
  
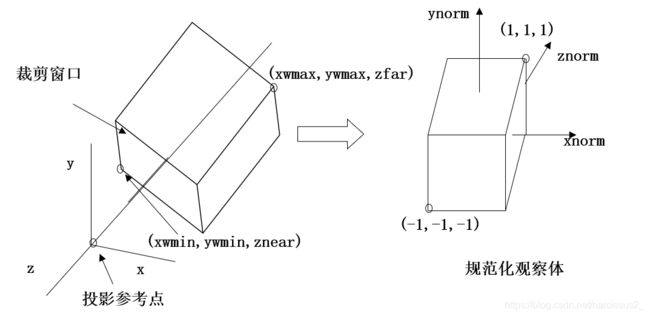
• 于是乎$(x_{wmin},y_{wmin},z_{near})$全部映射到了$(-1,-1.-1)$,$(x_{wmax},y_{wmax},z_{far})$全部映射到了$(1,1,1)$
  
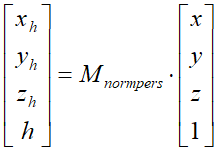
• 又是一个坐标系转换，无非套用上面的公式，最后得到结果
  
• 一旦我们完成了对标准化投影坐标的转换，剪切就可以应用于对称立方体（或单位立方体）。
• 标准化视图体积的内容可以转移成屏幕坐标。

3 总结：

• 3D场景的查看过程遵循2D查看中使用的一般方法，我们创建世界坐标场景，然后设置查看坐标参考框架和传输对象描述，3D观察需要投影例程并涉及更多空间参数
• 使用相机类比来描述3D观察参数，其中使用视图参考点（摄像机位置），视平面法线向量N（摄像机镜头方向）和查看向量V（视图向量V）建立视图坐标参考系。相机朝上）
• 可以用投影向量指定平行投影（正交或倾斜）
• 利用在投影参考点处相交的投影线获得对象的透视投影
• 平行投影保持物体比例，但透视投影减小了远处物体的尺寸
• 如果线不与视平面平行，则透视投影会使平行线收敛到消失点。

参考资料：

http://glasnost.itcarlow.ie/~powerk/GeneralGraphicsNotes/projection/orthographicprojection.html
https://blog.csdn.net/smilejiasmile/article/details/79606234
https://blog.csdn.net/Goncely/article/details/5397729
http://glasnost.itcarlow.ie/~powerk/GeneralGraphicsNotes/projection/orthographicprojection.html
https://blog.csdn.net/qq_16334327/article/details/81228679
https://blog.csdn.net/caoshangpa/article/details/80272903
《计算机图形学：原理及实践》
三维观察ppt

图片自制或取于网络素材