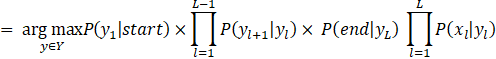HMM及维特比算法
参考
HMM：https://blog.csdn.net/sinat_25346307/article/details/79119366
Viterbi算法：https://blog.csdn.net/shenxiaoming77/article/details/79228378
一、HMM定义 以词性标注为例说明
图1 词性标注任务
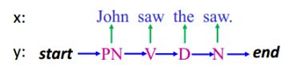
1、问题：如图1所示，已知x，求x的词性标注y。
该问题转化为数学语言即为：在已知x的条件下计算得y的最大概率，如公式(1)所示
|
|
(1) |
由条件概率公式可得公式(2)
|
|
(2) |
由于x是已知的，所以公式(2)中的p(x)可以省去，故公式(2)可以用公式(3）
|
|
(3) |
在HMM中，我们实际使用公式(4)的形式来求解，公式(3)使用条件概率公式可得公式(4)
|
|
(4) |
2、HMM是一种有监督学习，需要有训练数据训练参数。
图2为一条训练数据，已知句子x的词性y，其中PN为名词，V为动词，D为冠词，N为名词。
图2已知句子x的词性y
可得P(y)公式(5)
|
|
(5) |
则可得
公式(6)
|
|
(6) |
将其一般化，可将第一步的概率P(y)称为转移概率(transition probability)，第二步的概率
称为输出概率(emission probability)。其概率值都可以通过训练数据得到。
第1步P(y) 转移概率可表示为公式(7)
|
|
(7) |
第2步
输出概率可表示为公式(8)
|
|
(8) |
将公式(7)(8)带入公式(4)即为HMM模型，如公式(9)所示。
| |
(9) |
二、HMM具体举例，使用Viterbi算法
1、问题
假设已知：
第1天小明感觉正常。
第2天小明感觉有点冷。
第3天小明觉有点头晕。
小明的身体观察序列x为：正常、冷、头晕
小明身体的隐藏状态有2种分别为：健康、发烧
求已知x的情况下，推断出小明每一天的身体状态呢?
2、转化为数学语言
正常、冷、头晕分别用0、1、2表示；健康、发烧分别用A、B表示。
则小明的观察序列x为：0，1，2
小明身体的隐藏状态有2种分别为：A、B
已知概率：
1）初始概率
| |
| |
2）转移概率
| |
| |
3）输出概率
| |
| |
3、问题进一步具体化
求：推断出小明每一天的身体状态呢?
已知：观察序列x和HMM模型。HMM模型即为初始概率、转移概率、输出概率。
4、求解，使用维特比算法
1）第1天 l=1， 
取值为0， 
的取值为A或B
由HMM模型公式(9)可得到公式(10)
|
|
(10) |
注意：这里
实际为
当
时, 带入公式(10)可得到公式(11)
| |
(11) |
当
时, 带入公式(10)可得到公式(12)
|
|
(12) |
2）第2天 l=2，
取值为1， 
的取值为A或B
由HMM模型公式(9)可得到公式(13)
|
|
(13) |
1、）当
时,公式(13)可化为公式(14)
| |
(14) |
公式(14)中的
可取A或B，此时由公式(9)可得公式(15)
| |
(15) |
由公式(15)可看出，当
取A时，
概率最大，记录此条路径。
这里在解释一下:
当前观测值为1，假定当前隐含状态为健康A，求当前的联合概率分布
。首先从昨天的状态到当前的健康A状态有两种路径(昨天的状态还没确定，而只是先计算出每个状态的概率分布)： 昨天健康A ----> 今天健康A， 昨天发烧 B-----> 今天健康A。 这两个路径分别的概率为 0.3 * 0.7 以及 0.04 * 0.4， 可以看到 当前如果为健康A时，昨天为健康A的概率更大，因此我们选定昨天健康 A----> 今天健康A 这条路径，即记录下当前为健康A时，昨天也为健康A状态， 然后求得当前的联合概率分布
= （0.3 * 0.7 ） * 0.4即如下：
= max{0.3*0.7, 0.04*0.4} * 0.4=0.3* 0.7 * 0.4=0.084
此时我们需要记录概率最大的路径的前一个状态，即0.084路径的前一个状态，我们在小本本上记下，第二天健康A时，第一天的状态也为健康A。
2、）当
时,公式(13)可化为公式(16)
| |
(16) |
公式(16)中的
可取A或B，此时由公式(9)可得公式(17)
| |
(17) |
由公式(17)可看出，当
取A时，
概率最大，记录此条路径。
一样的道理，从昨天的状态到当前的发烧B状态也有两种路径： 昨天健康A ----> 今天发烧B， 昨天发烧B -----> 今天发烧B，这两个路径分别的概率为 0.3 * 0.3以及 0.04 * 0.6， 可以看到 当前如果为发烧B时，昨天为健康A的概率更大，因此我们选定昨天健康A ----> 今天发烧B 这条路径，即记录下当前为发烧B时，昨天也为健康B状态， 当前的联合概率分布
= （0.3 * 0.3 ） * 0.3， 即如下：
= max{0.3*0.3, 0.04*0.6} * 0.3=0.027,
同样的在0.027这个路径上，第二天为发烧B时，第一天也是健康A的。
3) 第3天 l=3， 
取值为2， 
的取值为A或B
由HMM模型公式(9)可得到公式(18)
| |
(18) |
1、） 
的取值为A，公式(18)可化为公式(19)
| |
(19) |
公式(19)中的
可取A或B，此时由公式(9)可得公式(20)
| |
(20) |
由公式(20)可看出，当
取A时，
取A时；
概率最大，记录此条路径。
2、） 
的取值为B，公式(18)可化为公式(21)
| |
(21) |
公式(21)中的
可取A或B，此时由公式(9)可得公式(22)
| |
(22) |
由公式(22)可看出，当
取B时，
取A时；
概率最大，记录此条路径。
4）到第三天是最后一天， 此时看第三天为发烧B时状态概率最大，即为最优状态，即P(最优)=0.01512，这样我们可以得到最优路径的终点，是发烧B状态。
由最优状态开始回溯。根据前面所记录的， 在求得第三天发烧的时候，我们记录的第二天最大概率的状态为健康A，因此确定第二天为健康A状态，继续回溯，当第二天为健康A状态时，我们记录的第一天是健康A的。这样，我们的状态序列逆推出来了。即为：健康A，健康A，发烧B；这就是小明这3天的身体状态。
5）别人也给出了一个HMM概率图 可以参考下：
图3 HMM概率图