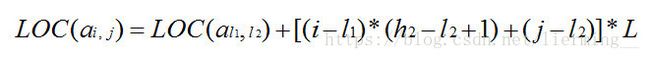特殊矩阵和压缩存储--------使用数组存储矩阵中的元素

         矩阵在计算机图形学、工程计算中占有举足轻重的地位。在数据结构中考虑的是如何用最小的内存

  空间来存储同样的一组数据。所以，不需要研究矩阵及其运算等，而把精力放在如何将矩阵更有效地存储

  在内存中，并能方便地提取矩阵中的元素。

----------数组的定义

         数组是由 n ( n >= 1 ) 个相同类型的数据元素构成的有限序列，每个数据元素称为一个数组元素，每个

    元素受 n 个线性关系的约束，每个元素在  n 个线性关系中的序号称为该元素的下标，并称该数组为 n 维

    数组。

         数组与线性表的关系 ： 数组是线性表的推广。一维数组可以看做是一个线性表；二维数组可以看做

    元素是线性表的线性表，依次类推。数组一旦被定义，它的维数和维界就不再改变。因此，除了结构的

   初始化和销毁之外，数组只会有存取元素和修改元素的操作。

----------数组的存储结构

        大多数计算机语言都提供了数组数据类型，逻辑意义上的数组可以采用计算机语言中的数组数据类型进行

   存储，一个数组的所有元素在内存中占有一段连续的存储空间。

        以一维数组  A[ 0...n-1 ] 为例，其存储结构关系为：

        LOC( a(i) ) =  LOC(a0)  + i * L （ 0 <=  i  < n）

         其中，L是每个数组元素所占存储单元。

      对于多维数组，有两种映射方法：按行优先和按列优先。以二维数组为例，按行优先存储的基本思想是：

 先行后列，先存储行号较小的元素，行号相等存储列号较小的元素。

      设二维数组的行下标和列下标的范围分别为 [ l1 , h1 ]  与 [ l2 , h2 ]  ，则存储结构关系为：

      

      假设 l1 和 l2 的值均为 0 ，则上式变为：

         

        当以按列优先存储时，得出存储结构关系式为：

       

  ---------矩阵的压缩存储

       压缩存储：指为多个值相同的元素只分配一个存储空间，对零元素不分配存储空间。其目的是为了

                     节省存储空间。

      特殊矩阵：指具有许多相同矩阵元素或零元素，并且这些矩阵元素或零元素的分布有一定规律性的

                     矩阵。常见的特殊矩阵有对称矩阵、上（下）三角矩阵 、 对角矩阵等。

     特殊矩阵的压缩存储方法：找出特殊矩阵中值相同的矩阵元素的分布规律，把那些呈现规律性分布的

                                           值相同的多个矩阵元素压缩到一个存储空间中。

     》》》 对称矩阵

            若一个 n 阶方阵 A[ 1....n ] [ 1......n ] 中任一个元素 a（i ，j）  都有  a( i , j ) = a( j , i ) 则称其

     为对称矩阵。

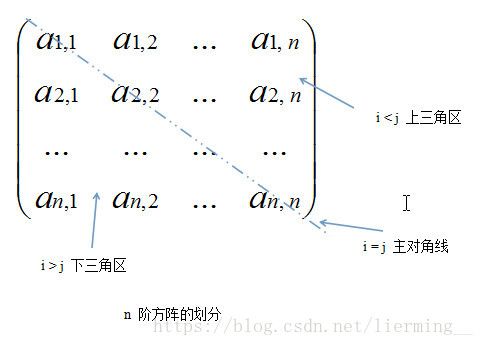
            对于一个 n 阶方阵 ，其中元素可以划分为 3 个部分，即上三角区、主对角线和下三角区，如下图

    所示：

           

           对于 n 阶对称矩阵，上三角区所有元素和下三角区对应元素相同，如果还采用二维数组存放，就会

     浪费几乎一半的空间我，为此将对称矩阵 A[ 1.....n ][ 1......n ] 存放在一个一维数组 B[ n (n+2) / 2 ] 中，

     即元素 a（i ， j） 存放在 b（k） 中。只存放主对角线和下三角区的元素。

           第 1 行：   1个元素   a(1,1)

           第 2 行：   2 个元素  a(2,1) , a(2,2)

           ...........................................

           第 i-1 行：  i -1 个元素

           第 i 行： j -1 个元素

         故，元素 a( i , j ) 在数组 B 中的下标 k = 1+2+...+( i-1 ) + j -1 = i ( i-1 ) / 2 +j -1  （数组下标从 0 开始）

      因此，元素下标之间的对应关系如下：

        

     》》》上（下）三角矩阵

           *** 下三角矩阵，如下图所示，上三角区的所有元素均为同一个常量。其存储思想为与对称矩阵类似，不同

                之处在于存储完下三角区和主对角线上的元素之后，紧接着存储对角线上 的常量一次，故可以将下三角

                矩阵 A[ 1........n ] [ 1........n ] 压缩存储在 B [ n ( n+1 ) / 2  +1 ] 中。

                 

                元素下标之间的对应关系为：

               

                下三角矩阵在内存中的压缩存储形式如下图：

                

         *** 上三角矩阵，如下图所示，下三角区的所有元素均为同一个常量。只需要存储主对角线、上三角

              区上的元素和下三角区的常量一次，可以将其压缩存储在 B [ n ( n+1 ) / 2  +1 ] 中。

             

             元素下标之间的对应关系如下：

                  

             上三角矩阵的在内存中的压缩存储形式如图：

                  

   

            补充：以上推导均假设数组的下标是从 0 开始，若题设有要求，则应该灵活应付。

》》》对角矩阵

            对角矩阵也称为带状矩阵。对于 n 阶方阵 A 中的任一元素 a( i , j ) ,当 | i - j | > 1  时，有

        a( i , j )  = 0 （1 <= i  , j <=  n）则称为三对角矩阵，如下图所示。在三对角矩阵中，所有非

       零元素都集中在以主对角线为中心的 3 条对角线的区域中，其他区域的元素都为 零 。

           

            对角矩阵也可以采用压缩存储，将 3 条对角线上的元素按行优先方式存在一维数组 B  中，且 a(1,1)

        存放于 B[ 0 ] 中，其存储形式如图：

           

           由此可以计算矩阵 A 中 3 条对角线上的元素 a( i , j ) ( 1 <= i  , j  <= n  , | i - j | < 1 ) 在一维数组

      B 中存放的下标为  。

           反之，若已知三对角线矩阵中某元素 a( i , j ) 在一维数组 B 中存放于第 k 个位置，则可求得

     

 

----------稀疏矩阵

       矩阵元素个数 s 相对于矩阵中非零元素个数 t 来说非常多，即 s >> t  矩阵称为稀疏矩阵。例如，

   若一个矩阵的阶为 100*100  ，而该矩阵中只有少于 100 个非零元素。

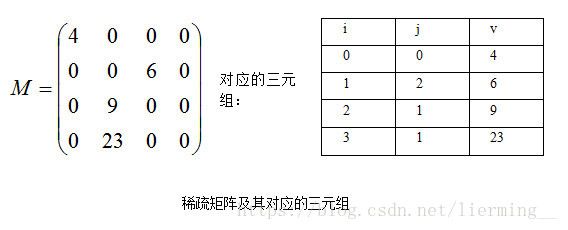
       如果采用常规的方法存储稀疏矩阵，那将相当浪费存储空间，因此仅存储非零元素。但通常非零

   元素的分布没有规律，所以，仅存储非零元素的值是不够的，还要存储它所在的行和列。因此，将

   非零元素及其相应的行和列构成一个三元组（行标，列标，值），如下图所示，然后再按照某种规律

   存储这些三元组。稀疏矩阵压缩存储后便失去了随机存取特性。