《数据结构与算法》课程设计//赫夫曼编码/译码器

《数据结构与算法》课程设计

一、 题目：赫夫曼编码/译码器

1.问题描述

利用赫夫曼编码进行通信可以大大提高信道利用率，缩短信息传输时间，降低传输成本。这要求在发送端通过一个编码系统对待传输数据预先编码，在接收端将传来的数据进行译码（复原）。对于双工信道（即可以双向传输信息的信道），每端都需要一个完整的编/译码系统。试为这样的信息收发站编写一个赫夫曼码的编/译码系统。

二、 实验目的

1.基本要求

一个完整的系统应具有以下功能：
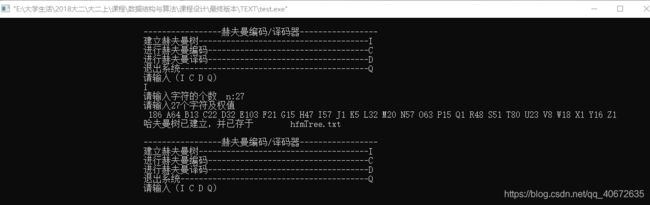
(1) I：初始化（Initialization）。从终端读入字符集大小n，以及n个字符和n个权值，建立赫夫曼树，并将它存于文件hfmTree中。
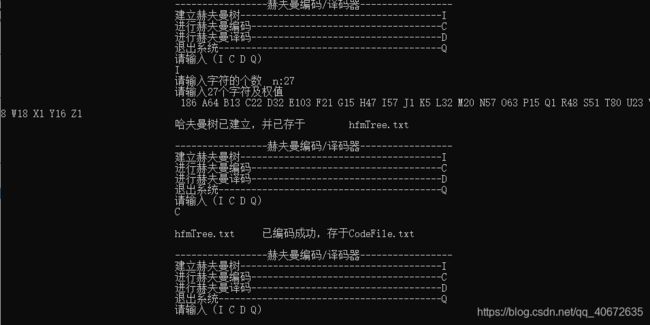
(2) E：编码（Encoding）。利用已建好的赫夫曼树（如不在内存，则从文件hfmTree中读入），对文件ToBeTran中的正文进行编码，然后将结果存入文件CodeFile中。
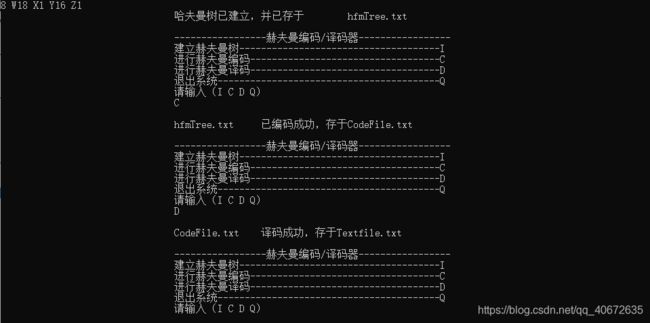
(3) D：译码（Decoding）。利用已建好的赫夫曼树将文件CodeFile中的代码进行译码，结果存入文件Textfile中。
以下为选做：
(4) P：打印代码文件（Print）。将文件CodeFile以紧凑格式显示在终端上，每行50个代码。同时将此字符形式的编码文件写入文件CodePrin中。
(5) T：打印赫夫曼树（Tree printing）。将已在内存中的赫夫曼树以直观的方式（比如树）显示在终端上，同时将此字符形式的赫夫曼树写入文件TreePrint 中。

2.测试要求

（1）已知某系统在通信联络中只可能出现八种字符，其频率分别为0.05、0.29、0.07、0.08、0.14、0.23、0.03、0.11，试设计赫夫曼编码。
(2) 用下表给出的字符集和频度的实际统计数据建立赫夫曼树，并实现以下报文的编码和译码：“THIS PROGRAME IS MY FAVORITE”。
字符 A B C D E F G H I J K L M
频度 186 64 13 22 32 103 21 15 47 57 1 5 32 20
字符 N O P Q R S T U V W X Y Z
频度 57 63 15 1 48 51 80 23 8 18 1 16 1

3.实现提示

(1) 编码结果以文本方式存储在文件Codefile中。
(2) 用户界面可以设计为“菜单”方式：显示上述功能符号，再加上“Q”，表示退出运行Quit。请用户键入一个选择功能符。此功能执行完毕后再显示此菜单，直至某次用户选择了“Q”为止。
(3) 在程序的一次执行过程中，第一次执行I，D或C命令之后，赫夫曼树已经在内存了，不必再读入。每次执行中不一定执行I命令，因为文件hfmTree可能早已建好。

三、 需求分析

《数据结构与算法》是计算机科学与技术专业重要的核心课程之一，在计算机专业的学习过程中占有非常重要的地位。《数据结构与算法课程设计》就是要运用本课程以及到目前为止的有关课程中的知识和技术来解决实际问题。特别是面临非数值计算类型的应用问题时，需要选择适当的数据结构，设计出满足一定时间和空间限制的有效算法。
本课程设计要求同学独立完成一个较为完整的应用需求分析。并在设计和编写具有一定规模程序的过程中，深化对《数据结构与算法》课程中基本概念、理论和方法的理解；训练综合运用所学知识处理实际问题的能力，强化面向对象的程序设计理念；使自己的程序设计与调试水平有一个明显的提高。

四、 概要设计

(1) typedef struct{
int weight;
char Data; //存放节点的字符
int Parent,Lchild,Rchild;
}HTNode,*HuffmanTree;

(2) typedef char** HuffmanCode;
(3) void HuffmanCoding(HuffmanTree &,char *,int *,int);
(4) void select(HuffmanTree HT,int j,int *s1,int *s2); //选择父母为 0且权值最小的两个结点
(5) void Initialization(); // 初始化赫夫曼树
(6) void Coding(); //赫夫曼编码
(7) void Decoding(); //赫夫曼译码
(8) void find(HuffmanTree &HT,char *code,char *text,int i,int m);
(9) HuffmanTree HT;
(10) int n=0; //赫夫曼树叶子结点数目
(11) int main()//主函数

五、 程序说明

本程序是一个赫夫曼编码/译码器，利用Initialization函数，初始化建立赫夫曼树，利用Coding函数进行赫夫曼编码，Deconding函数进行赫夫曼译码。其中Coding函数中涉及select函数，select函数的用途是寻找父母为0且权值最小的两个结点。Decongding函数中涉及find函数，find函数的主要功能是通过递归的方式，在赫夫曼树中寻找赫夫曼码所对应的字符，并写入到Textfile.txt中。

六、 详细设计

#include
#include
#include

typedef struct{
	int weight; 
	char Data; 													//存放节点的字符 
	int Parent,Lchild,Rchild; 
}HTNode,*HuffmanTree; 

typedef char** HuffmanCode; 
void HuffmanCoding(HuffmanTree &,char *,int *,int);
void select(HuffmanTree HT,int j,int *s1,int *s2);   //选择父母为 0且权值最小的两个结点 
void Initialization(); 										   // 初始化赫夫曼树 
void Coding(); 														//赫夫曼编码  
void Decoding(); 													//赫夫曼译码
void find(HuffmanTree &HT,char *code,char *text,int i,int m);
HuffmanTree HT; 
int n=0; 												  //赫夫曼树叶子结点数目

//------------------------------------------------------------------------------
																		//主函数 

int	main()
{
	char T;
	while (1)
	{	
		printf("\n");
		printf("\t\t\t\t-----------------赫夫曼编码/译码器-----------------\n");
		printf("\t\t\t\t建立赫夫曼树-------------------------------------I\n");
		printf("\t\t\t\t进行赫夫曼编码-----------------------------------C\n");
		printf("\t\t\t\t进行赫夫曼译码-----------------------------------D\n");
		printf("\t\t\t\t退出此程序---------------------------------------Q\n");
		printf("\t\t\t\t请输入（I C D Q）                          \n\t\t\t\t"); 
		scanf("%c",&T);	
		switch(T)			
		{							
			case 'I':				
				Initialization();				
				break ;				
			case 'C':				
				Coding();			
				break ;				
			case 'D':				
				Decoding();			
				break ;				
			case 'Q':				
				exit(1);				
			default		:				
				printf(	"\t\t\t\t输入错误 \n" );		
		}							
		getchar();
	}
	return	0;
}

//------------------------------------------------------------------------------
                   //初始化函数，输入n个字符及其对应的权值，根据权值建立赫夫曼树

void Initialization()
{
	
	FILE *fp;
	int	i,w[52];												//存放字符的权值 
	char character[52];											 // 存放 n个字符
	printf("\t\t\t\t请输入字符的个数:");	
	scanf("%d",&n);			
	printf("\t\t\t\t请输入%d个字符及权值:\n\t\t\t\t" ,n);
	for(i=0;i<n;i++)					
	{					
		char  b=getchar();  		
		scanf("%c" ,&character[i]);			
		scanf("%d",&w[i]);								 // 输入字符和对应的权值
	}					
	HuffmanCoding(HT,character,w,n);							     // 建立赫夫曼树
	if ((fp=fopen("hfmTree.txt","w"))==NULL) 
		printf("\t\t\t\thfmTree.txt	打开失败 \n"  );	
	for(i=1;i<=2*n-1;i++)				
	{					
		if(fwrite(&(HT[i].Data),sizeof (char),1,fp)!=1)
			printf(	"\t\t\t\t写入文件失败  \n");	
		if(fwrite(&(HT[i].weight),sizeof(int),1,fp)!=1)
			printf(	"\t\t\t\t写入文件失败  \n");	
		if(fwrite(&(HT[i].Parent),sizeof(int),1,fp)!=1)
			printf(	"\t\t\t\t写入文件失败  \n");	
		if(fwrite(&(HT[i].Lchild),sizeof(int),1,fp)!=1)
			printf(	"\t\t\t\t写入文件失败  \n");	
		if(fwrite(&(HT[i].Rchild),sizeof(int),1,fp)!=1)
			printf(	"\t\t\t\t写入文件失败  \n");		
	}					
	printf("\t\t\t\t赫夫曼树已建立，并已存于 hfmTree.txt\n");
	fclose(fp);					

}

//------------------------------------------------------------------------------
															//建立赫夫曼树的算法

void HuffmanCoding(HuffmanTree &HT,char *character, int *w, int n)
{
	int	m,i,s1,s2;
	HuffmanTree p;
	if(n<=1)
		return  ;
	m=2*n-1;
	HT=(HuffmanTree)malloc((m+1)* sizeof(HTNode));
	for(p=HT+1,i=1;i<=n;++i,++p,++character,++w)					   // 赋初值 
	{
		p->Data=*character;
		p->weight=*w;
		p->Parent=0;
		p->Lchild=0;
		p->Rchild=0;
	} 
	for(;i<=m;++i,++p)								   // 给后面的节点赋初值为 0 
	{
		p->Data=0;
		p->weight=0;
		p->Parent=0;
		p->Lchild=0;
		p->Rchild=0;
	} 
	for(i=n+1;i<=m;++i)										   // 生成新节点
	{
		select(HT,i-1,&s1,&s2);	
		HT[s1].Parent=i;HT[s2].Parent=i;
		HT[i].Lchild=s1;HT[i].Rchild=s2;
		HT[i].weight=HT[s1].weight+HT[s2].weight;
	} 
}

//------------------------------------------------------------------------------
											  //选择父母为 0且权值最小的两个结点

void select(HuffmanTree HT,int j, int *s1, int *s2)
{
	int	i;
	for(i=1;i<=j;i++)
		if (HT[i].Parent==0)
		{
			*s1=i;
			break;
		} 
	for(;i<=j;i++)
		if((HT[i].Parent==0)&&(HT[i].weight<HT[*s1].weight))
		*s1=i;									// 则 s1为最小结点的序号
	HT[*s1].Parent=1;	// 提前给 HT[*s1].Parent	赋值 1，以免找次小结点、 判断条件时受影响
		
		
	for(i=1;i<=j;i++)
		if(HT[i].Parent==0)
		{
			*s2=i;
			break;
		} 					   // 有一个没访问过的就跳出循环，以此为起点比较
	for(;i<=j;i++)
		if((HT[i].Parent==0)&&(i!=*s1)&&(HT[i].weight<HT[*s2].weight))
		*s2=i;									  // 找weight 次小的结点
}

//------------------------------------------------------------------------------
//进行赫夫曼编码

void Coding()
{
	FILE *fp,*fw;
	int	i,f,c,r,start;
	char *cd;
	char temp;
	HuffmanCode HC;
	{
		HC=(HuffmanCode)malloc((n+1)* sizeof (char*));
		cd=(char *)malloc(n*sizeof(char));
		cd[n-1]='\0';
		for(i=1;i<=n;++i)
		{
			start=n-1;
			for(c=i,f=HT[i].Parent;f!=0;c=f,f=HT[f].Parent)
				if (HT[f].Lchild==c)
					cd[--start]='0';
				else
					cd[--start]='1';
			HC[i]=(char *)malloc((n-start)* sizeof(char));  
			strcpy(HC[i],&cd[start]);	
		}
		free(cd);
	}
		if((fp=fopen("ToBeTran.txt","rb"))==NULL) 
			printf("\t\t\t\tToBeTran.txt 打开失败 \n");	
		if((fw=fopen("CodeFile.txt","wb+"))==NULL) 	 // 建立新文件进行读/ 写
			printf("\t\t\t\tCodeFile.txt 打开失败 \n");
		fscanf(fp,"%c",&temp);	// 从fp 所指的文件中读入第一个字符到	temp变量
		while(!feof(fp))
		{
			for(i=1;i<=n;i++)
				if (HT[i].Data==temp)
					break ;						   // 若和 1号节点相同则跳出循环
			for(r=0;HC[i][r]!='\0';r++)	// 在赫夫曼树中查找字符所在的位置
				fputc(HC[i][r],fw);	// 将字符对应的编码存入文件，把	HC[i][r]	写到 fw所指示文件
			fscanf(fp,"%c",&temp);					 // 从文件读入下一个字符
		}
		fclose(fw);
		fclose(fp);
		printf("\n\t\t\t\thfmTree.txt	已编码成功，存于CodeFile.txt\n"	);
}

//------------------------------------------------------------------------------
//进行赫夫曼译码

void Decoding()
{
	FILE *fp,*fw;
	int	m,i;
	char *code,*text,*p;
	if((fp=fopen("CodeFile.txt","rb"))==NULL) 			     // 打开文件进行只读
		printf("\t\t\t\tCodeFile.txt	打开失败 \n");
	if((fw=fopen("Textfile.txt","wb+"))==NULL) // 建立新文件读  / 写, 若已建立，内容会清空
		printf(	"\t\t\t\tTextfile.txt	打开失败 \n");
	code=(char*)malloc(sizeof(char));
	fscanf(fp,"%c",code);							 // 从文件读入一个 0或 1字符
	for(i=1;!feof(fp);i++)
	{
		code=(char *)realloc(code,(i+1)*sizeof(char));	
		fscanf(fp,"%c",&code[i]);			     // 从文件读入下一个 0或 1的字符
	}
	//	至此 CodeFile.txt文件中的 0、 1已全部读入，存放在  code数组中
	text=(char *)malloc(100*sizeof(char));
	p=text;
	m=2*n-1;
	if(*code=='0')
		find(HT,code,text,HT[m].Lchild,m);				   // 从根节点的左子树找
	else
		find(HT,code,text,HT[m].Rchild,m);				   // 从根节点的右子树找
		
	for(i=0;p[i]!='\0';i++)		       // 把译码好的字符存入文件 Textfile.txt 中
		fputc(p[i],fw);						   	// 把 p[i]写到 fw所指示的文件中
	fclose(fp);
	fclose(fw);
	printf(	"\n\t\t\t\tCodeFile.txt	译码成功，存于Textfile.txt\n"	);
}

//------------------------------------------------------------------------------
//译码时根据 01字符串寻找相应叶子节点的递归算法

void find(HuffmanTree &HT,char *code,char *text,int i, int m)
{
	if(*code!='\0')											 // 若译码未结束
	{
		code++;
		if(HT[i].Lchild==0&&HT[i].Rchild==0)				   // 若找到叶子节点
		{
			*text=HT[i].Data;					   	// 将叶子节点字符存入text 中
			text++;
			if((*code=='0'))
				find(HT,code,text,HT[m].Lchild,m);	   // 继续从根节点的左子树找
			else
				find(HT,code,text,HT[m].Rchild,m);	   // 继续从根节点的右子树找
		}
		else	
 			if(*code=='0')
				find(HT,code,text,HT[i].Lchild,m);	     	 // 从该节点左子树找
			else
				find(HT,code,text,HT[i].Rchild,m);			 // 从该节点右子树找
	}
	else
		*text='\0';
}

七、 调试分析

由所给的字符和权值建立赫夫曼树

由所建立的哈弗曼树编码 hfmtree.txt:

由哈弗曼树和哈弗曼编码译码 codefile.txt:

八、 实验心得与体会（总结）