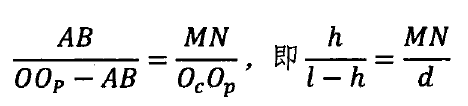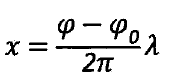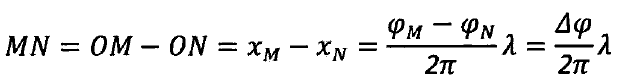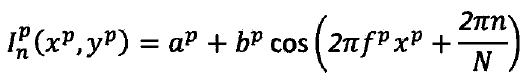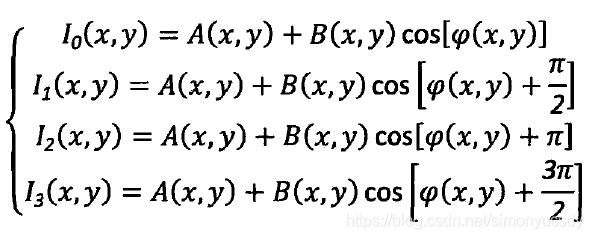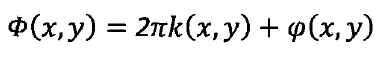结构光三维重建系统综述

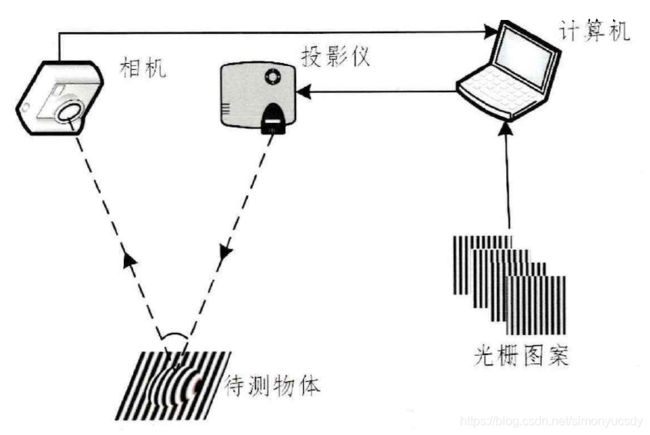
数字光栅投影（Digital Fringe Projector，DFP）三维测量系统主要由相机、投影设备(Projector)和计算机三部分组成，如图所示。首先在计算机端进行结构光图案编码，再由投影设备将编码图案投射到待测物体表面，因物体表面的高度变化将会对投射的条纹图像产生调制，然后由相机获取被调制的条纹图案传输到计算机进行条纹处理，计算出相位的分布，最后由相位和高度的映射关系求出待测物体的表面的高度。

相移法（Phase Shift），是通过对投影的光栅条纹进行一定的相移，然后投射多幅相移图案到有形变物体的表面，最后通过求解相位场的分布得到物体表面的三维深度信息，因其精度高适用于漫反射物体测量，这种方法最为常用。基于相移法的光栅投影三维重建系统，核心的工作包括系统校正、相机标定和解相位等关键技术。

1 数学建模

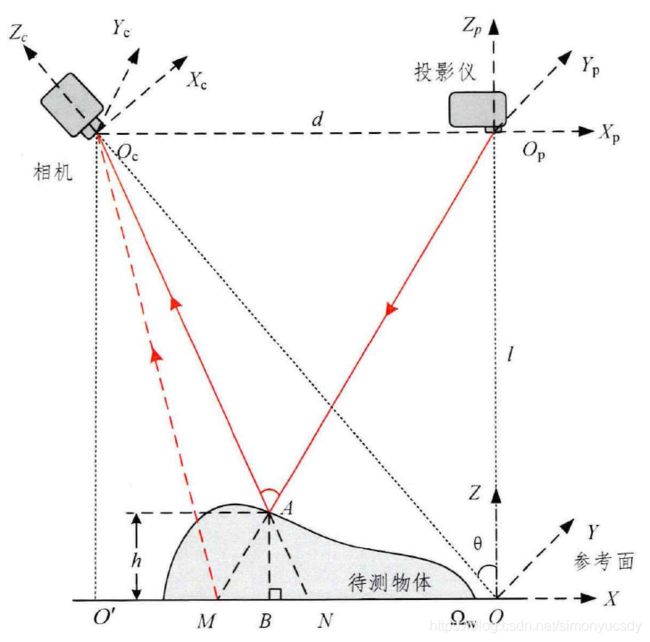
根据数字光栅投影系统模型组成及原理，建立维测量系统的几何模型如下图，Qw为参考坐标系OXYZ，其中XOY为参考平面，为参考坐标系，为投影仪坐标系。Oc、Op分别为相机（Camera）、投影仪（Projector）的光心，在参考面上的投影为，为待测物体上的任意一点。平面均平行于纸面。

其工作流程如下，假设开始参考平面上没有物体，从投影仪端有一束入射光线OpA投射到点Ｍ，此时在相机视野中对应该光线的投射点为参考面的点Ｍ，当放置待测物体后，该光线投射到物体表面上的A点，若相机和投影的角度保持不变，此时从相机端获取图片，由于物体高度的变化，在相机视野中对应该光线的原投射点Ｍ平移到了点N，点N为反射光线的反向延长线与参考面的交点。由于从点Ｍ到点N的位移携带了点A相对于参考平面的高度信息h，即AB的长度，由几何关系我们可以根据位移ＭN求得高度h。而位移ＭN的长度又和投影光栅紧密相连，基于此，下面建立高度和相位的映射关系的数学模型。

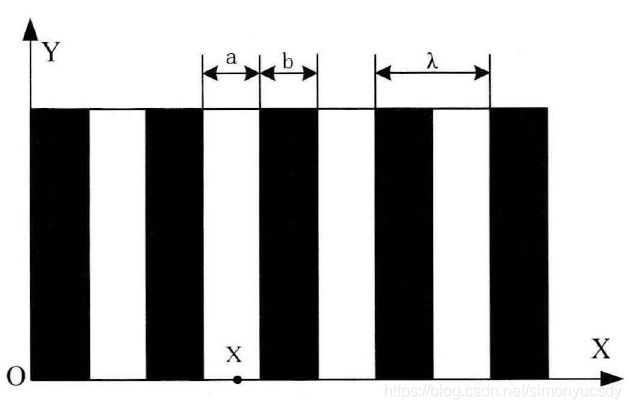
投射光栅条纹的分布如下图，ａ为线间缝宽，ｂ为栅线宽，Ａ为光栅节距。

有相似三角形性质可得到：三角形AMN~三角形AOcOp，于是有：

当参投影面和参考平面XOY平行时，投射的光栅相位将沿参考平面X轴方向变化，设平面上任一点相位为，根据光栅条纹分布特性可得：

为原点O0的初始相位。

带入到高度的换算公式中：

上式即为数字光栅投影测量法中高度和相位映射关系的核心表达式，为相位差，其中系统参数、、可以通过标定得到，而是在参考平面XOY的相位，也可通过标定获得，是在经待测物体调制后的相位，属于待求解量。

2 相对相位主值求解（求包裹相位）

相移法通过向待测物体投射系列正弦条纹，假设在投影空间中有一点，那么该点灰度值可用数学表达式表示为：

 Ｎ为相移总步数，n表示第ｎ次相移，n=1,2,3\...,N-1，ap为背景灰度值或直流分量，bp为调制强度或幅度。在条纹投射到待测物体表面之后，由相机端检测到的产生形变的条纹图像函数可表示为：

为待求相位主值，因此要求解，至少需要三幅图像。由上式可以求得标准N步相移法表达式：

以四步相移法为例，当N=4时，相位移间隔为，则四幅光栅图像的相位移依次是０，，，，对应的光强依次为：

3 解包裹相位

相位解包裹（Phase Unwrapping）求解是DFP三维测量技术中的关键步骤之一，也是研究热点和难点。

在光栅投影阶段采用标准Ｎ步相移法，为了恢复相位，这些方法均采用反正切函数逐像素计算相对相位主值，以至于求解的相位的值域在范围内，在这个阶段获得的相位称为包裹相位(Wrapped Phase)，要利用相位和高度的映射关系求解三维坐标，被包裹的相位必须恢复为完整的相位场，称为解包裹或解相位。

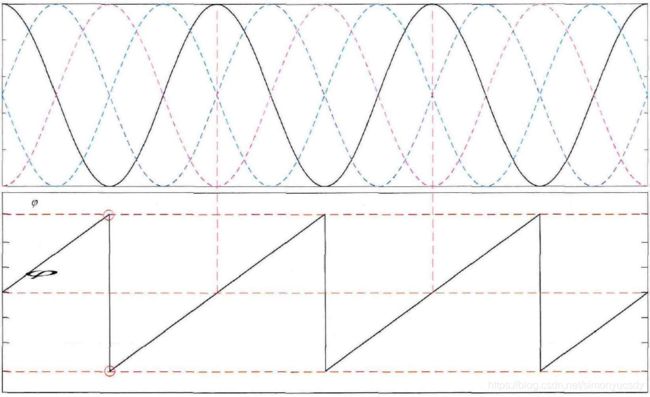
以四步相移法为例，由相移光栅计算得到的相对相位主值（包裹相位）显示如下图，从图中可以看出相对相位主值在不连续的地方相差，且这种不连续呈周期分布。

在实际情况中，相位主值除了在单个周期内连续分布外，在沿整个Ｘ方向分布也是连续的，我们发现相位突变的地方，相位值加上的整数倍即可得到实际的连续相位值，其数学表达式如下：

k是观察点的条纹级次。如果条纹图像中每一点处的条纹级次都有一个预设值且唯一确定，那么求得的连续称为绝对相位值（Absolute Phase），相位解包裹的本质也就是求解图像中每一点的条纹级次。

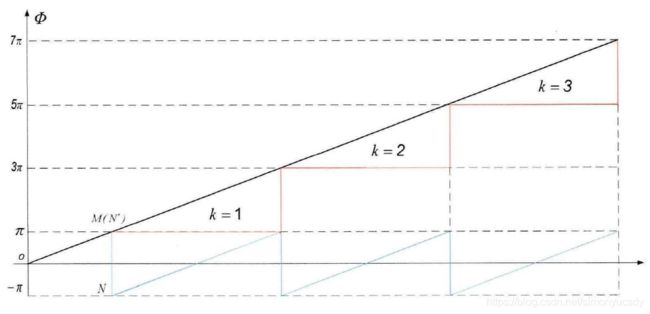
绝对相位值求解过程可得到如下图所示的绝对相位主值图，其函数曲线也由周期间断的锯齿形变为连续上升的直线，且条纹级次的变化依次递增。

4 相位解包裹方法

传统的相位解包裹方法可以分为两类：空间相位展开和时间相位展开。时间相位展开算法源于激光干涉测量法，且只能用于正弦光栅条纹，例如多频相移法。

格雷码法：

多频外差法：

5 误差分析及校正