复数基础——复数的绝对值,复数的极坐标形式的直观解释练习_8
目录
复数的绝对值
复数的极坐标形式的直观解释练习
复数的绝对值
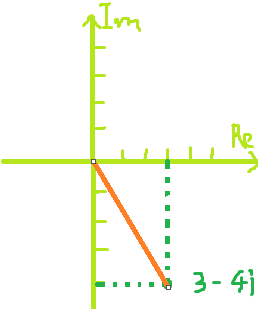
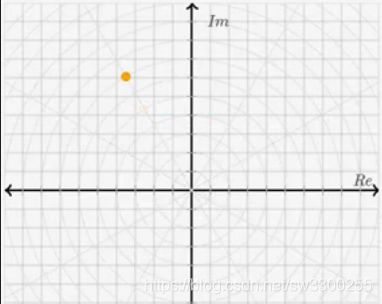
已知复数![]() ,我把它在复平面上标出来了:
,我把它在复平面上标出来了:
实部是3,也就是实轴上标注3,虚部是-4,纵轴向下4,这就是已知复数点 ![]() ,我们要求的是
,我们要求的是![]() 。不管是实数绝对值,还是复数绝对值,就是这点在坐标平面上到原点的距离,那么
。不管是实数绝对值,还是复数绝对值,就是这点在坐标平面上到原点的距离,那么![]() 的绝对值就等于
的绝对值就等于![]() 这一点在复平面上的位置到原点的距离:
这一点在复平面上的位置到原点的距离:
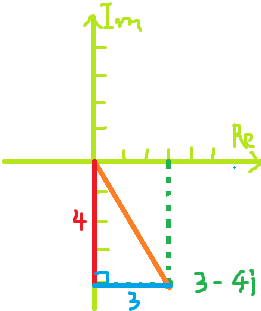
那么橙色这一段就是 ![]() 的绝对值,这段距离要怎么求?我们可以找到一个直角三角形然后用勾股定理来求,大家看,要建立一个直角三角形的话,这段距离,从0到-4,所以距离是4。
的绝对值,这段距离要怎么求?我们可以找到一个直角三角形然后用勾股定理来求,大家看,要建立一个直角三角形的话,这段距离,从0到-4,所以距离是4。
直角三角形的底边,从0到3,距离就是3,这就是直角:
这条边是水平的,红色边是垂直的,下面可以用勾股定理来求![]() 了,这点到原点的距离就是直角三角形的斜边长度,那么借助勾股定理,两直角边的平方:
了,这点到原点的距离就是直角三角形的斜边长度,那么借助勾股定理,两直角边的平方:
刚已经说过了,绝对值就是求距离,绝对值一定是正值(至少是非负值),所以等式两边开平方,取正平方根,取正平方根的话,25开平方是5:
或者这么说,这段距离就是5,这个长度是5,好,假设我们没有画图,还有一种直接的计算方法。当然,实虚部还是已知的,我们可以把实虚分别平方,加和,然后开平方。如果大家不想画图看一下,可以直接这么做,实际刚刚我们也是这么算的。
我们来做一下:实部平方 虚部平方 加和,然后开平方:
复数的极坐标形式的直观解释练习
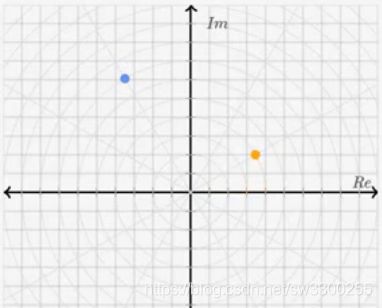
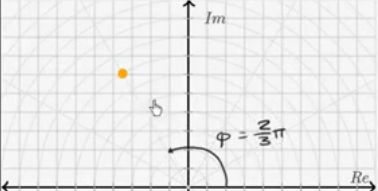
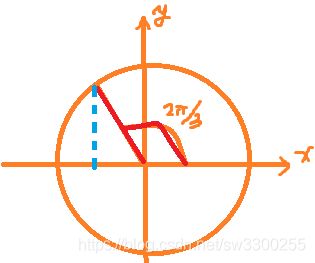
题目要求我们调整橙色复数的模和角度,也就是图中的橙色的点:
来跟蓝色的复数点![]() 重合,也就是这个点,要弄明白这个坐标,我们先标一下坐标轴,纵轴是虚轴,横轴是实轴,蓝色复数,实部为3.5,这个我们已经在复平面上做出来了,虚部是6.06。很明显,题目的作图方式是极坐标的方式,同时告诉我们,可以调整复数的角度,极坐标中复数的角度,我们通常称作辅角,半径叫做模,下面我们来调整一下橙色点的位置。
重合,也就是这个点,要弄明白这个坐标,我们先标一下坐标轴,纵轴是虚轴,横轴是实轴,蓝色复数,实部为3.5,这个我们已经在复平面上做出来了,虚部是6.06。很明显,题目的作图方式是极坐标的方式,同时告诉我们,可以调整复数的角度,极坐标中复数的角度,我们通常称作辅角,半径叫做模,下面我们来调整一下橙色点的位置。
大家看,如果增大半径,点就会外延,
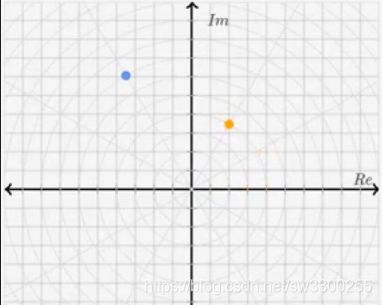
而增大角度的话,比如3/π,
在增大成π/2:
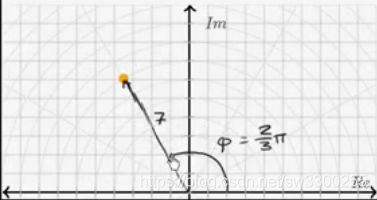
直接变成2π/3。这样的复数的角度就对了,只要再增大半径就可以重合了:
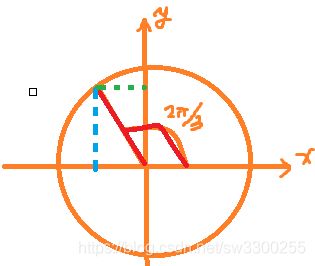
好的,重合时半径是7,角度是2π/3,下面来看,这个橙色点的复数是否就等于题目给的复数,橙色的点复数不仅在直角坐标系中,在具有实虚轴的复平面也表示了,下面我们来演算一下,我们来验证一下两个复数是不是相等的。
那么,这个辅角,在复平面中,这个角,我们一般用![]() 代表,
代表,![]() :
:
这个角度是弧度制的,模,就是指原点到该点的长度,通过这个工具,我们知道这个长度是7,
下面来验证一下,这个复数确实等于![]() ,这个点的位置,模是7,辅角已知,可以用7乘以e的辅角次方表示:
,这个点的位置,模是7,辅角已知,可以用7乘以e的辅角次方表示:
而根据欧拉公式,欧拉公式是数学史上非常著名非常有用的公式,这就等于:
确实,这里系统写的复数与我们得到的一致。下面来求![]() 和
和![]() 分别等于多少。
分别等于多少。
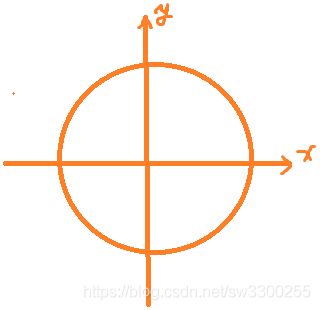
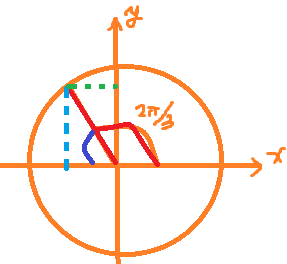
既然要求某个角的正余弦,不可避免我们要想到单位圆,角度是![]() ,我先画一个单位圆,希望大家不要把直角坐标系和刚我们研究的极坐标系混淆了,这不是极坐标系,因为表示的不是复数,这就是我们之前介绍过的单位圆,这是x轴,y轴:
,我先画一个单位圆,希望大家不要把直角坐标系和刚我们研究的极坐标系混淆了,这不是极坐标系,因为表示的不是复数,这就是我们之前介绍过的单位圆,这是x轴,y轴:
![]() 也就是120°,有点类似左边极坐标的表示,这个角度
也就是120°,有点类似左边极坐标的表示,这个角度![]() 。
。
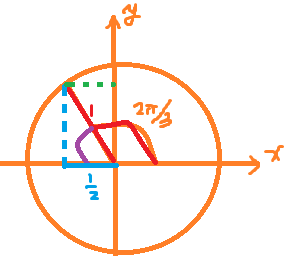
x坐标是什么呢?这个角度120°的话,这个角就是60°。
所以这是有30-60度角的特殊直角三角形,因为这是单位圆,所以半径就是1,30度角的对边就是斜边的一半,也就是1/2:
所以这个坐标是-1/2,而60度角的对边就是![]() ,所以这个距离是
,所以这个距离是![]() ,大家可以在计算器上算一下:
,大家可以在计算器上算一下:
根据我们找到的条件,那么得出:
来看这个复数是不是等于题目给的复数:
实部是相同的,都是-3.5,下面用计算器计算一下![]() ,虚部是不是在6.06左右,经过计算之后,确实等于6.06。得到的复数确实约等于
,虚部是不是在6.06左右,经过计算之后,确实等于6.06。得到的复数确实约等于![]() 。跟题目给的信息一致的。
。跟题目给的信息一致的。
——请不断重复练习、练习、练习、再练习。。。