【双目视觉探索路6】整体代码结构分析与作业完成(未完待续)
上一节的程序实现了立体视觉实现过程的所有步骤,现在对整体框架进行分析学习
书中框架结构介绍
书:Learning OpenCV3
第一步:读取左右图像对
目的:寻找亚像素精度的circles
方法:调用stereoCalibrate()标定
需求:相机矩阵_M以及畸变矢量_D
输出:_R,_T,_E,_F
第二步:评估精度
方式:图像上的点距离另一张图像上的极线到底有多远。
调用函数 undistortPoints()以及computeCorrespondEpilines()
第三步:计算校正图像
方式
Hartley-> cv::stereoRectifyUncalibrated()
如果使用这一步,代码还需要计算基础矩阵或者直接调用立体标定得到的基础矩阵
然后调用cv::remap()计算校正图像。
本实例中通过划线,表明了校正图像之间的联系。
Bouguet->stereoRectify()
第四步:计算视差图
这一部分通过StereoSGBM()寻找标定/非标定的校正立体图像对的视差图。
例子中给了水平放置以及垂直放置相机的校正实例。
但是垂直放置只能通过非标定校正算法,除非你通过代码对图像进行了转换
StereoCalib开放接口
接口参数表
static void StereoCalib(const char *imageList, int nx, int ny,
bool useUncalibrated)在主程序中,使用了StereoCalib函数,使用形式为
StereoCalib(board_list, board_w, board_h, true);其中board_list为包含了标定板名称的txt文件;board_w,board_h为棋盘格的方格数目,最后一个参数为校正的形式(使用标定校正(Bouguet's algorithm)还是非标定校正(Hartely's algorithm))
StereoCalib内部分析
工作流程
程序的流程为双目立体视觉成像的流程:
单目标定(获取内外参)->双目标定(相机之间的转换矩阵)->校正(输出行对准图像)->立体匹配(输出深度图)
立体校正的两种方法
前面几篇文章只是泛泛的提了一下立体校正,本文由于是进一步深入的应用,将对涉及的两种校正方法:Bouguet算法以及Hartely算法进行原理上的梳理。
资料来源:
Learning OpenCV3
Hartely算法(Hartley's algorithm)
本文研究的主程序对useUncalibrate赋值为true,进入程序中则自动选择非标定校正算法;这里采用的非标定校正算法就是Hartley算法。
Hartley算法通过将极点匹配到无穷远的方法寻找单应性,可以减少两立体图像之间的视差。这种方法绕过了计算相机的内参,从而不用进行点的匹配,因此算法复杂度较低。基础矩阵可由stereoCalibrate()获得。
优点:通过简单的观察场景中的点,可以实现在线立体标定(online stereo calibrate)
缺点:由于避开了图像的内参调用;我们无法了解图像的尺度因子,比如棋盘格到底是距离我们100cm还是100m。
函数
Bouguet算法(Bouguet's algorithm)
Bouguet算法就是标定算法,其输入参数为两相机之间的R/T矩阵。立体矫正在Bouguet算法的实现原理是:在最大化公共视场区域的同时,最小化重投影畸变。
由于目前我的数学基础还不扎实,以及目前这部分是为了用;这两种算法的原理在后续继续深入研究时将进行补充。
函数
本文调用函数汇总
stereoCalibrate
本函数实现立体标定,输出R、T、E、F矩阵
stereoRectifyUncalibrated
本函数实现Hartley's algorithm进行立体校正标定
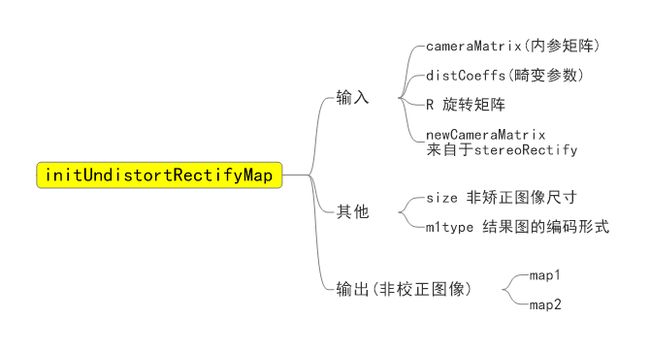
initUndistortRectifyMap
该函数的目的为获取校正图像,需求流程如下:
上述图像为立体矫正的过程。立体校正的流程为:原始图像a经过去畸变得到b,b再经过校正获得行对准图像c,c再经过裁剪获得最终图像d.
校正计算的过程则为c->a的过程。
在获得了立体标定项后,通过调用initUndistortRectifyMao能够预先计算从相机角度的左右查找图。对于任何图像-图像的匹配函数,前向匹配(由原图像计算到目标图像)会由于浮点的影响使信息丢失,从而使得目标图像更像一块奶酪。
在立体校正的过程中,我们将调用这个函数两次(分别对应于左右相机)
函数原型
remap
remap是一个基础的重映射函数,相关内容可以参考 OpenCV中的重映射:remap()函数
原型为
void remap(InputArray src, OutputArray dst, InputArray map1, InputArray map2,
int interpolation, intborderMode = BORDER_CONSTANT,
const Scalar& borderValue = Scalar())前两个参为输入输出矩阵;map1与map2可为映射矩阵模式,也可为图像色彩格式;第五个参数为插值方式;第六个参数为边界模式;第七个参数为边界颜色,默认Scalar()黑色。
具体例子不再拓展
StereoSGBM
函数上一节讲过,虽然用的比较笨,后续将进行继续修炼。
数据流
该部分目的是在梳理重建的过程中回归到作业中来。
作业
需了解及完成步骤
1,如何利用立体校正的方法获取前向平行图像?
2,如何用SGBM的方法获取视差图?
分步解决
早上键盘alt被默认锁定了,半天没打开,后面通过连按两次alt解除了锁定。废话不多说,直接进入正文
控制台窗口显示图像:
首先输出序列标定图像得到相应的内外参,然后running stereo calibration获得内外参后,获得重投影误差avg err,最后是校正与视差图获取。
调用函数第一项:stereoCalibrate
这部分调用的函数使用方法为
stereoCalibrate(
objectPoints, points[0], points[1], M1, D1, M2, D2, imageSize, R, T, E, F,
TermCriteria(TermCriteria::COUNT | TermCriteria::EPS, 100, 1e-5),
CALIB_FIX_ASPECT_RATIO | CALIB_ZERO_TANGENT_DIST |
CALIB_SAME_FOCAL_LENGTH
);
也就是为下面的校正与匹配提供了R,T,E,F四个矩阵
传递给第二项stereoRectify
回忆前文
Hartley-> cv::stereoRectifyUncalibrated()
如果使用这一步,代码还需要计算基础矩阵或者直接调用立体标定得到的基础矩阵
然后调用cv::remap()计算校正图像。
本实例中通过划线,表明了校正图像之间的联系。
实现
三个点:
1,基础矩阵
2,remap()计算校正图像
3,图像划线
coding
vector allpoints[2];
for (i = 0; i < nframes; i++) {
copy(points[0][i].begin(), points[0][i].end(),
back_inserter(allpoints[0]));
copy(points[1][i].begin(), points[1][i].end(),
back_inserter(allpoints[1]));
}
cv::Mat F = findFundamentalMat(allpoints[0], allpoints[1], cv::FM_8POINT);
cv::Mat H1, H2;
cv::stereoRectifyUncalibrated(allpoints[0], allpoints[1], F, imageSize,
H1, H2, 3);
R1 = M1.inv() * H1 * M1;
R2 = M2.inv() * H2 * M2;
// Precompute map for cvRemap()
//
cv::initUndistortRectifyMap(M1, D1, R1, P1, imageSize, CV_16SC2, map11,
map12);
cv::initUndistortRectifyMap(M2, D2, R2, P2, imageSize, CV_16SC2, map21,
map22);
// RECTIFY THE IMAGES AND FIND DISPARITY MAPS
//
cv::Mat pair;
if (!isVerticalStereo)
pair.create(imageSize.height, imageSize.width * 2, CV_8UC3);
else
pair.create(imageSize.height * 2, imageSize.width, CV_8UC3); 下一步:继续拆分程序进行解读
首先应当删除一些不需要的程序,然后进行分段test!梳理好思路,结合书上
12.27任务:
完成一对图像的校正与DepthMap生成的过程
分析代码段
// CALIBRATE THE STEREO CAMERAS
Mat M1 = Mat::eye(3, 3, CV_64F);
Mat M2 = Mat::eye(3, 3, CV_64F);
Mat D1, D2, R, T, E, F;
cout << "\nRunning stereo calibration ...\n";
stereoCalibrate(
objectPoints, points[0], points[1], M1, D1, M2, D2, imageSize, R, T, E, F,
TermCriteria(TermCriteria::COUNT | TermCriteria::EPS, 100, 1e-5),
CALIB_FIX_ASPECT_RATIO | CALIB_ZERO_TANGENT_DIST |
CALIB_SAME_FOCAL_LENGTH
);
//参数对应
//输入:objectPoints, imagePoints 1,2 双相机矩阵M1,D1 M2,D2 imageSize
//输出 R T E F
int nframes = (int)objectPoints.size();
// COMPUTE AND DISPLAY RECTIFICATION
//
if (showUndistorted) {
cv::Mat R1, R2, P1, P2, map11, map12, map21, map22;
//Hartley's Uncalibrated
vector allpoints[2];
for (i = 0; i < nframes; i++) {
copy(points[0][i].begin(), points[0][i].end(),
back_inserter(allpoints[0]));
copy(points[1][i].begin(), points[1][i].end(),
back_inserter(allpoints[1]));
}
cv::Mat F = findFundamentalMat(allpoints[0], allpoints[1], cv::FM_8POINT);
cv::Mat H1, H2;
cv::stereoRectifyUncalibrated(allpoints[0], allpoints[1], F, imageSize,
H1, H2, 3);
R1 = M1.inv() * H1 * M1;//inv()求逆
R2 = M2.inv() * H2 * M2;
// Precompute map for cvRemap()
//
cv::initUndistortRectifyMap(M1, D1, R1, P1, imageSize, CV_16SC2, map11,
map12);//相机内参矩阵,即便系数矩阵,一二相机之间的旋转矩阵,输入的矫正后的相机矩阵,无失真矩阵
cv::initUndistortRectifyMap(M2, D2, R2, P2, imageSize, CV_16SC2, map21,
map22);
// RECTIFY THE IMAGES AND FIND DISPARITY MAPS
//
cv::Mat pair;
if (!isVerticalStereo)
pair.create(imageSize.height, imageSize.width * 2, CV_8UC3);
else
pair.create(imageSize.height * 2, imageSize.width, CV_8UC3);
// Setup for finding stereo correspondences
//
StereoSGBM sgbm;
int SADWindowSize = 9;
//预处理sobel,获得图像梯度信息,用于计算代价
sgbm.preFilterCap = 63;
//代价参数,得到SAD代价
int numberOfDisparities = 64;
sgbm.SADWindowSize = SADWindowSize > 0 ? SADWindowSize : 3;
sgbm.minDisparity = 0;
sgbm.numberOfDisparities = numberOfDisparities;
//动态规划参数,默认四条路径
IplImage *img1 = cvLoadImage("left01.jpg", 0);
int cn = img1->nChannels;
sgbm.P1 = 8 * cn*sgbm.SADWindowSize*sgbm.SADWindowSize;
sgbm.P2 = 32 * cn*sgbm.SADWindowSize*sgbm.SADWindowSize;
//后处理参数,唯一性检测、亚像素插值、左右一致性检测、连通区域检测
sgbm.uniquenessRatio = 10;
sgbm.speckleWindowSize = 100;
sgbm.speckleRange = 32;
sgbm.disp12MaxDiff = 1;
Mat disp, disp8;
for (i = 0; i < nframes; i++) {
Mat img1 = imread(imageNames[0][i].c_str(), 0);
Mat img2 = imread(imageNames[1][i].c_str(), 0);
Mat img1r, img2r, disp, vdisp;
if (img1.empty() || img2.empty())
continue;
remap(img1, img1r, map11, map12, cv::INTER_LINEAR);
remap(img2, img2r, map21, map22, cv::INTER_LINEAR);
if (!isVerticalStereo) {
sgbm(img1r, img2r, disp);
cv::normalize(disp, vdisp, 0, 256, cv::NORM_MINMAX, CV_8U);
imshow("disparity", vdisp);
}
if (!isVerticalStereo) {
cv::Mat part = pair.colRange(0, imageSize.width);
cvtColor(img1r, part, cv::COLOR_GRAY2BGR);
part = pair.colRange(imageSize.width, imageSize.width * 2);
cvtColor(img2r, part, cv::COLOR_GRAY2BGR);
for (j = 0; j < imageSize.height; j += 16)
cv::line(pair, cv::Point(0, j), cv::Point(imageSize.width * 2, j),
cv::Scalar(0, 255, 0));
}
else {
cv::Mat part = pair.rowRange(0, imageSize.height);
cv::cvtColor(img1r, part, cv::COLOR_GRAY2BGR);
part = pair.rowRange(imageSize.height, imageSize.height * 2);
cv::cvtColor(img2r, part, cv::COLOR_GRAY2BGR);
for (j = 0; j < imageSize.width; j += 16)
line(pair, cv::Point(j, 0), cv::Point(j, imageSize.height * 2),
cv::Scalar(0, 255, 0));
}
cv::imshow("rectified", pair);
if ((cv::waitKey() & 255) == 27)
break;
}
} 函数总结如下,依次调用了下面三个函数:stereoRectifyUncalibrated, initUndistortRectifyMap和StereoSGBM
上面程序的核心在于
Mat disp, disp8;
for (i = 0; i < nframes; i++) {
Mat img1 = imread(imageNames[0][i].c_str(), 0);
Mat img2 = imread(imageNames[1][i].c_str(), 0);
Mat img1r, img2r, disp, vdisp;
if (img1.empty() || img2.empty())
continue;
remap(img1, img1r, map11, map12, cv::INTER_LINEAR);
remap(img2, img2r, map21, map22, cv::INTER_LINEAR);
if (!isVerticalStereo) {
sgbm(img1r, img2r, disp);
cv::normalize(disp, vdisp, 0, 256, cv::NORM_MINMAX, CV_8U);
imshow("disparity", vdisp);
}
if (!isVerticalStereo) {
cv::Mat part = pair.colRange(0, imageSize.width);
cvtColor(img1r, part, cv::COLOR_GRAY2BGR);
part = pair.colRange(imageSize.width, imageSize.width * 2);
cvtColor(img2r, part, cv::COLOR_GRAY2BGR);
for (j = 0; j < imageSize.height; j += 16)
cv::line(pair, cv::Point(0, j), cv::Point(imageSize.width * 2, j),
cv::Scalar(0, 255, 0));
}
else {
cv::Mat part = pair.rowRange(0, imageSize.height);
cv::cvtColor(img1r, part, cv::COLOR_GRAY2BGR);
part = pair.rowRange(imageSize.height, imageSize.height * 2);
cv::cvtColor(img2r, part, cv::COLOR_GRAY2BGR);
for (j = 0; j < imageSize.width; j += 16)
line(pair, cv::Point(j, 0), cv::Point(j, imageSize.height * 2),
cv::Scalar(0, 255, 0));
}
cv::imshow("rectified", pair);
if ((cv::waitKey() & 255) == 27)
break;
}最终能够获取视差图的核心语句为:
Mat img1 = imread("left01.jpg");
Mat img2 = imread("right01.jpg");
Mat img1r, img2r, disp1, vdisp;
remap(img1, img1r, map11, map12, cv::INTER_LINEAR);
remap(img2, img2r, map21, map22, cv::INTER_LINEAR);
sgbm(img1r, img2r, disp1);
cv::normalize(disp1, vdisp, 0, 256, cv::NORM_MINMAX, CV_8U);
imshow("disparity", vdisp);
waitKey(100000);其中normalize的作用为归一化,相当于matlab中的imshow(disp,[]);
继续向上走,可以整理得到这一段程序
由程序可知,map11\2和map21\2可通过initUndistortRectifyMap获得
于是本步骤目的为,如何获取map矩阵。
获得map矩阵的需求为M,D,R,P一共八个矩阵,为了更好地了解下作业怎么做,我们输出一下相关调用参数:
相机1
相机2
看看我们作业中有什么内容
作业中给出了旋转向量,而上述程序需要旋转矩阵,因此第一步为
向量到矩阵的转换
罗德里格斯变换
直接调用函数即可进行输出
Mat Rvl = (Mat_(1,3)<< 0.04345, -0.05236, -0.01810);
Mat RvTl;
cout << "Rvl=Rvr= " << endl << " " << Rvl << endl< 3,显示极线校正结果
4,用opencv3表示sgbm的内容
视差图转化为距离图
在实施的过程中发现需要调用重投影矩阵Q,而重投影矩阵Q似乎只能由校正算法(Bouguet's algorithm)获得
现在我们来学学Bouguet's algorithm
Bouguet's algorithm立体校正的原则为最大化视场的重叠区域以及最小化重投影步骤
为了最小化重投影畸变,旋转矩阵分为两半(左旋转矩阵和右旋转矩阵)
下一步,分析矩阵构成,输出Q矩阵
明日继续补充