【椭球大地测量学】Python及MATLAB实现大地坐标与空间直角坐标间的转换编程(含流程图)
目录
- 一、功能
- 二、使用方法
- 三、算法流程图
- 四、Python程序
- (1)计算程序
- (2)DOS接口程序
- 五、MATLAB程序
- (1)大地坐标转换为空间直角坐标
- (2)空间直角坐标转换为大地坐标
- 六、运行结果
- 1、Python运行结果
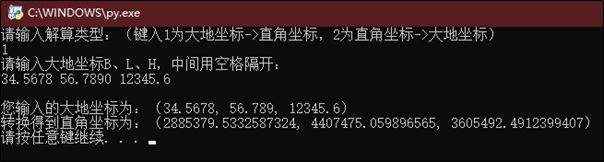
- (1)大地坐标转换为空间直角坐标
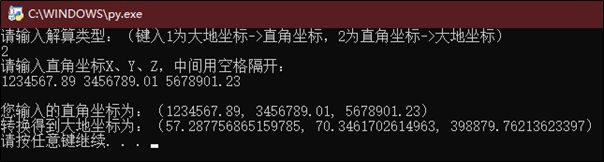
- (2)空间直角坐标转换为大地坐标
- 2、MATLAB运行结果
- (1)大地坐标转换为空间直角坐标
- (2)空间直角坐标转换为大地坐标
- 七、文件下载地址
一、功能
使用Python实现大地坐标与空间直角坐标间的转换,使用CGCS2000国家大地坐标系的椭球数据。
功能为:
①已知某点的大地坐标(L,B,H),求该点相应的大地空间直角坐标(X,Y,Z)
②已知某点的大地空间直角坐标(X,Y,Z),求该点相应的大地坐标(L,B,H)
二、使用方法
将文件计算程序与接口程序放在同一文件夹下,双击即可运行接口程序。
(注:该程序包含计算程序和接口程序,用户可以通过调整接口程序创建属于自己的交互界面。流程图在下载的压缩文件中。)
三、算法流程图
四、Python程序
(1)计算程序
import math as m
class Earth():
# 建立椭球类,,采用SGCS2000中国大地坐标系数据
def __init__(self): # 给定椭球数据
# 长半轴
self.a = 6378137.0
# 短半轴
self.b = 6356752.31414
# 扁率
self.f = 1/298.257222101
# 第一偏心率的平方
self.e1s = m.pow(0.0818191910428, 2)
# 第二偏心率的平方
self.e2s = self.e1s / (1 - self.e1s)
class Transform():
# 建立转换类
def __init__(self): # 导入椭球数据
self.earth = Earth()
def BLH_XYZ(self, B, L, H): # 大地坐标转换为空间直角坐标
# 将角度转换为弧度
self.b = m.radians(B)
self.l = m.radians(L)
# 计算辅助函数
self.W = m.sqrt(1 - self.earth.e1s * m.pow(m.sin(self.b), 2))
# 转换为空间直角坐标
self.N = self.earth.a / self.W
self.X = (self.N + H) * m.cos(self.b) * m.cos(self.l)
self.Y = (self.N + H) * m.cos(self.b) * m.sin(self.l)
self.Z = (self.N * (1 - self.earth.e1s) + H) * m.sin(self.b)
def XYZ_BLH(self, X, Y, Z): # 空间直角坐标转换为大地坐标
# 求出大地经度
self.l = m.atan(Y / X)
# 求出大地纬度
self.r = m.sqrt(X * X + Y * Y)
self.tb1 = Z / self.r
while True:
self.tb2 = 1 / self.r * (
Z + self.earth.a * self.earth.e1s * self.tb1 /
m.sqrt(1 + self.tb1 * self.tb1 * (1 - self.earth.e1s)))
if abs(self.tb2 - self.tb1) <= 5e-10:
break
self.tb1 = self.tb2
self.b = m.atan(self.tb2)
# 求出大地高
self.W = m.sqrt(1 - self.earth.e1s * m.pow(m.sin(self.b), 2))
self.N = self.earth.a / self.W
self.H = self.r / m.cos(self.b) - self.N
# 将弧度转换为角度
self.B = m.degrees(self.b)
self.L = m.degrees(self.l)
class Point():
# 建立点类
def BLH(self, B, L, H): # 建立直角坐标点类
self.B = B
self.L = L
self.H = H
self.P = Transform()
self.P.BLH_XYZ(B, L, H)
self.X = self.P.X
self.Y = self.P.Y
self.Z = self.P.Z
def XYZ(self, X, Y, Z): # 建立直角坐标点类
self.X = X
self.Y = Y
self.Z = Z
self.P = Transform()
self.P.XYZ_BLH(X, Y, Z)
self.B = self.P.B
self.L = self.P.L
self.H = self.P.H
(2)DOS接口程序
import CoordinateTransformation
import sys as s
import os
SolveType = input('请输入解算类型:(键入1为大地坐标->直角坐标,2为直角坐标->大地坐标)\n')
while True:
if SolveType == '1':
# 当选择'大地坐标->直角坐标'模式时
# 输入大地坐标
I = input('请输入大地坐标B、L、H,中间用空格隔开:\n')
while True:
if I:
pass
else:
s.exit(0)
try:
[B, L, H] = [float(n) for n in I.split()]
break
except:
I = input('输入错误,请重新输入大地坐标B、L、H,中间用空格隔开:\n')
else:
pass
# 开始转换
P = CoordinateTransformation.Point()
P.BLH(B, L, H)
B = str(B)
L = str(L)
H = str(H)
X = str(P.X)
Y = str(P.Y)
Z = str(P.Z)
massege = '\n您输入的大地坐标为:(' + B + ', ' + L + ', ' + H + ')\n转换得到直角坐标为:(' + X + ', ' + Y + ', ' + Z + ')'
print(massege)
break
elif SolveType == '2':
# 当选择'直角坐标->大地坐标'模式时
# 输入直角坐标
I = input('请输入直角坐标X、Y、Z,中间用空格隔开:\n')
while True:
if I:
pass
else:
s.exit(0)
try:
[X, Y, Z] = [float(n) for n in I.split()]
1/X
break
except:
I = input('输入错误,请重新输入直角坐标X、Y、Z,中间用空格隔开:\n')
else:
pass
# 开始转换
P = CoordinateTransformation.Point()
P.XYZ(X, Y, Z)
X = str(X)
Y = str(Y)
Z = str(Z)
B = str(P.B)
L = str(P.L)
H = str(P.H)
massege = '\n您输入的直角坐标为:(' + X + ', ' + Y + ', ' + Z + ')\n转换得到大地坐标为:(' + B + ', ' + L + ', ' + H + ')'
print(massege)
break
else:
SolveType = input('输入错误,请重新输入解算类型:(键入D为正算,I为反算)\n')
os.system('pause')
五、MATLAB程序
(1)大地坐标转换为空间直角坐标
% 大地坐标转换为空间直角坐标
clear all
clc
BLH = [34.5678, 56.7890, 12345.6];
% 键入需要转换的大地坐标(B,L,H)
format long g
XYZ = BLH_XYZ(BLH);
XYZ
%% 转换函数
function [XYZ] = BLH_XYZ(BLH)
% BLH_XYZ 大地坐标转换为直角坐标
% 导入CGCS2000的椭球数据
a = 6378137.0; % 长半轴
es = 0.0818191910428^2; % 第一偏心率的平方
B = BLH(1);
L = BLH(2);
H = BLH(3);
% 计算辅助函数
W = sqrt(1 - es * sind(B)^2);
% 转换为空间直角坐标
N = a / W;
X = (N + H) * cosd(B) * cosd(L);
Y = (N + H) * cosd(B) * sind(L);
Z = (N * (1 - es) + H) * sind(B);
XYZ = [X, Y, Z];
end
(2)空间直角坐标转换为大地坐标
% 空间直角坐标转换为大地坐标
clear all
clc
XYZ = [1234567.89, 3456789.01, 5678901.23];
% 键入需要转换的直角坐标(X,Y,Z)
format long g
BLH = XYZ_BLH(XYZ);
BLH
%% 转换函数
function [BLH] = XYZ_BLH(XYZ)
% XYZ_BLH 直角坐标转换为大地坐标函数
% 导入CGCS2000的椭球数据
a = 6378137.0; % 长半轴
es = 0.0818191910428^2; % 第一偏心率的平方
X = XYZ(1);
if X == 0
disp('输入错误')
return
end
Y = XYZ(2);
Z = XYZ(3);
% 求出大地经度
l = atan(Y / X);
L = l * 180 / pi;
% 求出大地纬度
r = sqrt(X^2 + Y^2);
tb1 = Z / r;
while true
tb2 = 1 / r * (Z + a * es * tb1 / sqrt(1 + tb1^2 *(1 - es)));
if abs(tb2 - tb1) <= 5e-10
break
else
tb1 = tb2;
end
end
b = atan(tb2);
B = b * 180 / pi;
% 求出大地高
W = sqrt(1 - es * sind(B)^2);
N = a / W;
H = r / cosd(B) - N;
BLH = [B, L, H];
end
六、运行结果
1、Python运行结果
(1)大地坐标转换为空间直角坐标
(2)空间直角坐标转换为大地坐标
2、MATLAB运行结果
(1)大地坐标转换为空间直角坐标
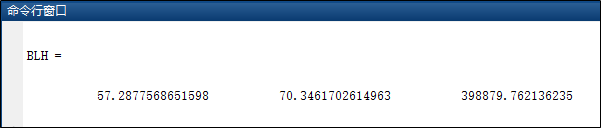
(2)空间直角坐标转换为大地坐标
七、文件下载地址
Python程序文件下载地址:【椭球大地测量学】Python实现大地坐标与空间直角坐标间的转换编程(含流程图)
MATLAB程序文件下载地址:【椭球大地测量学】MATLAB实现大地坐标与空间直角坐标间的转换编程(含流程图)