树和二叉树的操作(课堂笔记)
一、树的定义和基本术语
1. 树是n(n>=0)个结点的有限集。
2. 在一棵非空树中,有且仅有唯一的根(root)结点,除根结点外其余结点可分为m(m>0)个互不相交的有限集,它们本身 也是一棵树,称为树的子树(subtree)。
3. 基本术语
(1)结点的度(degree):结点所拥有的子树的数目;
(2)叶子结点(leaf node):度为0的结点;
(3)分支结点(branch node):度不为0的结点;
(4)孩子(child):结点的子树的根称为结点的孩子;
(5)双亲(parent):结点是其孩子的双亲;
(6)祖先(forefather):从树根到双亲的所有结点称为该结点的祖先;
(7)子孙(progeny):以结点为根的子树的所有结点称为该结点的子孙;
(8)兄弟(sibling):同一父母的所有孩子互称兄弟;
(9)层次(level):树根为第一层,孩子为第二层,以此类推;
(10)堂兄弟(cousin):双亲在同一层的结点互称堂兄弟;
(11)深度(depth):树中结点的最大层次称为树的深度;
(12)有序树(ordered tree):结点各子树从左至右是有秩序的树称为有序树;
(13)无序树(unordered tree):结点各子树没有秩序的树称为无序树;
(14)森林(forest):m (m≥0) 棵互不相交的树的集合。
二、二叉树
- 定义:二叉树(binary tree)是一棵度为二的树,其孩子有左右之分,也分别都是二叉树。
- 性质:(1) 在二叉树的第 i 层上最多有 2^(i -1) 个结点(i≥1);
(2) 深度为 k 的二叉树最多有 (2^k)-1个结点(k≥1);
(3) 对任一二叉树,叶子结点数为 n0,度为2的结点数为 n2,则 n0 = n2 +1。
(4)具有 n 个结点的完全二叉树的深度为 log2n +1向下取整;
(5)对一棵有 n 个结点的完全二叉树从上到下、从左到右进行连续编号,则对任一结点 i (1≤i≤n) 有:
① i=1的结点是树根,i>1 的结点的父母为 i / 2 向下取整;
② 若左右孩子存在,则分别为 2i 和 2i+1 结点。
3. 特殊二叉树:
(1)满二叉树(full binary tree):一棵深度为 k 且有 (2^k)-1个结点的二叉树称为满二叉树;
(2)完全二叉树(complete binary tree):一棵深度为 k 的满二叉树的第 k 层的右边几个结点不存在则为完全二叉树。
4. 二叉树的存储结构
(1)顺序存储结构:直接用数组从上到下、从左至右存;
(2)链式存储结构:结点域存数据、左孩子、右孩子;
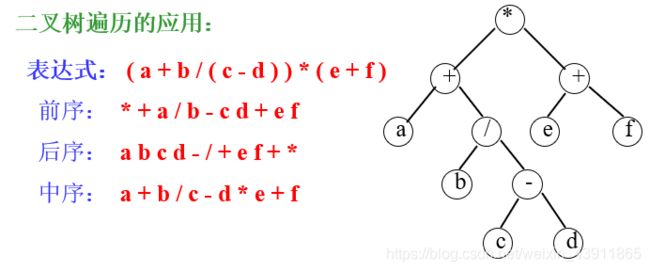
三、遍历二叉树和线索二叉树
遍历二叉树( traversing binary tree):即按某种搜索顺序对二叉树中每个结点访问且仅访问一次。
void Preorder ( struct node*t )
{//前序遍历
if ( t )
{
visit ( t );
Preorder (t->lchild);
Preorder (t->rchild);
}
}
void Inorder ( struct node*t )
{//中序遍历
if ( t )
{
Inorder (t->lchild);
visit ( t );
Inorder (t->rchild);
}
}
void Postorder ( struct node*t )
{//后序遍历
if ( t )
{
Postorder (t->lchild);
Postorder (t->rchild);
visit ( t );
}
}
void InOrderTraverse(BiTree T)
{//中序遍历二叉树的非递归算法
InitStack(S);
p = T;
while(p||!StackEmpty(S))
{
if(p)
{
Push(S, p);
p = p->lchild;//根指针进栈,遍历左子树
}
else
{
Pop(S, p);
if(!Visit(p->data))
return error;
p = p->rchild;//根指针退栈,访问根结点,遍历右子树
}
}
}
void LevelOrder ( struct node * t )
{// 按层次遍历的算法
Iniqueue( q);
if ( t )
Enqueue( q, t );
while (! Empty( q))
{
t = Dequeue( q);
visit( t );
if ( t-> lchild)
Enqueue( q, t -> lchild );
if ( t-> rchild)
Enqueue( q, t -> rchild );
}
}线索二叉树:一棵二叉链表表示的二叉树有 n+1 个空指针,可以利用这些空指针来存储结点的前驱和后继,这即是线索。为了区分到底是孩子指针还是线索,还需在每个结点内设置两个标志位 ltag 和 rtag,标志位为0,表示是孩子指针;标志位为 1,则表示是线索。其中 lchild 指向前驱,rchild 指向后继。
BiThrTree Pre;//刚刚访问过的结点
void InThreading(BiThrTree p)
{//中序遍历进行中序线索化
if(p)
{
InThreading(p->lchild);
//线索化操作开始
if(!p->lchild)
{
p->LTag = Thread;
p->lchild = pre;//左孩子指针指向前驱
}
if(!pre->rchild)
{
pre->RTag = Thread;
pre->rchild = p;//前驱右孩子指针指向后继
}
pre = p;//保持pre指向p的前驱
//线索化操作结束
InThreading(p->rchild);
}
}
void InOrderTraverse_Thr(BiThrTree T)
{//中序遍历二叉线索链表表示的二叉树T
BiThrTree p;
p = T->lchild;//p指向根节点
while(p!=T)//空树或遍历结束时,p==T
{
while(p->LTag==Link)//找到中序序列第一个结点
p = p->lchild;
while (p->RTag == Thread && p->rchild!=T)
{
p = p->rchild;
visit(p->data);
}
p = p->rchild;
}
}
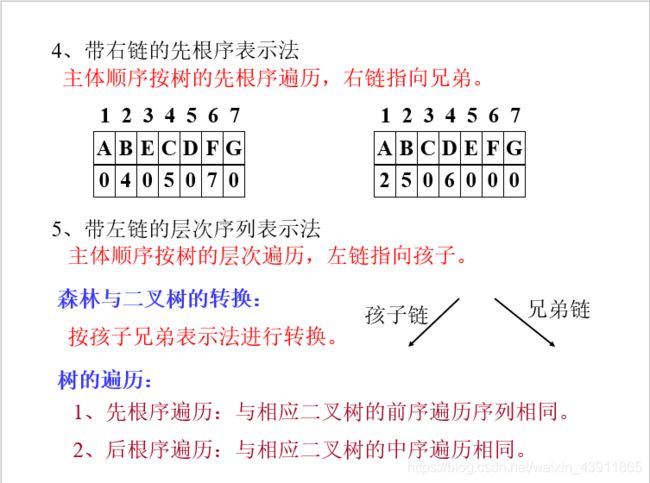
四、数与森林
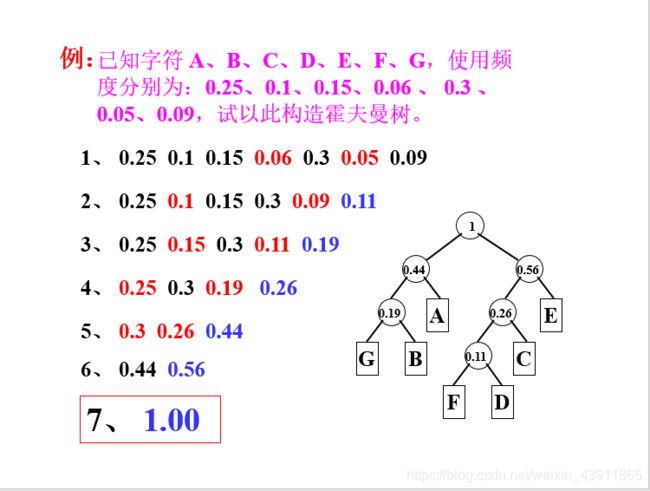
五、霍夫曼树及其应用
- 霍夫曼树(Huffman tree),也称最优树(optimal tree),是一种带权外路径长度(weighted path length)最短的树。
- 树的带权外路径长度是树中所有叶子结点的带权路径长度之和,即 叶子结点的数值 * 路径长度 的和。
- 霍夫曼树中除叶子结点外,所有分支结点的度均为 2,叶子结点(外部结点)可看成是由分支结点(内部结点)组成的树扩充出来的,因此,霍夫曼树是一棵扩充二叉树(extended binary tree)。