有趣的哈夫曼树和哈夫曼编码
一.哈夫曼树
哈夫曼树又称最优二叉树,是一类带权路径长度最短的树,有着广泛的应用,首先我们先学习一下与哈夫曼树有关的术语。
1.路径:从一个节点到另一个节点的分支。
2.路径长度:路径上的分支数目。
3.树的路径长度:从树根到每一节点的路径长度之和。
4.结点的带权路径长度:从该结点到树根之间的路径长度与结点上权的乘积,
5.树的带权路径长度:树中所有叶子结点的带权路径长度之和,通常记做WPL
6.哈夫曼树(最优二叉树):带权路径长度之和最小的二叉树
下面我们根据一道题来理解以上这些概念
如图有三棵二叉树,都有四个结点 a,b,c,d,分别带权7,5,2,4。求每棵树的带权路径长度

来我们算一下
第一棵树的WPL: 7 * 2+5 * 2+2 * 2+4 * 2=36
第二棵树的WPL:7 * 3+5 * 3+4 * 2+2 * 1=46
第三棵树的WPL: 7 * 1+5 * 2+2 * 3+4 * 3=35
通过计算我们可以知道第三棵树的带权路径长度最小,而且我可以告诉你,第三棵树恰好就是abcd这四个结点所能构造出的哈夫曼树。
所以哈夫曼树怎么构造呢?下面让我来好好唠唠!
7.哈夫曼树的构造方法
聪明的哈夫曼最早给出了一个带有一般规律的算法,江湖人称“哈夫曼算法”
(1)根据给定的n个权值{W1,W2,W3…Wn}构成n棵二叉树的集合F={T1,T2,T3…Tn},其中每棵二叉树Ti中只有一个带权为Wi的根节点,其左右子树均为空
(2)在F中选取两棵根节点的权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为其左右子树上根节点的权值之和
(3)在F中删除这两棵树,同时将新得到的二叉树加入F中
(4)重复(2)(3),直到F中只含一棵树为止,这棵树就是哈夫曼树
以上是哈夫曼树构造方法的官方语言,大家尽可能理解,如若理解不了,不要着急,这不是还有小编我呢么嘿嘿,下面是小编我自己的大白话解释
(1)将给定的n个权值 看做一个集合
(2)从集合中选出两个值最小的来作为二叉树的左右结点,然后左右结点的权值和作为根节点。
(3)将刚才选的两个数从集合中删去,将他们俩的和添加到集合中。
(4)重复以上过程,直至集合中剩一个数,构造完毕
大白话配套图文解释(此时应有掌声,小编画图小白,此时累倒在笔记本上)
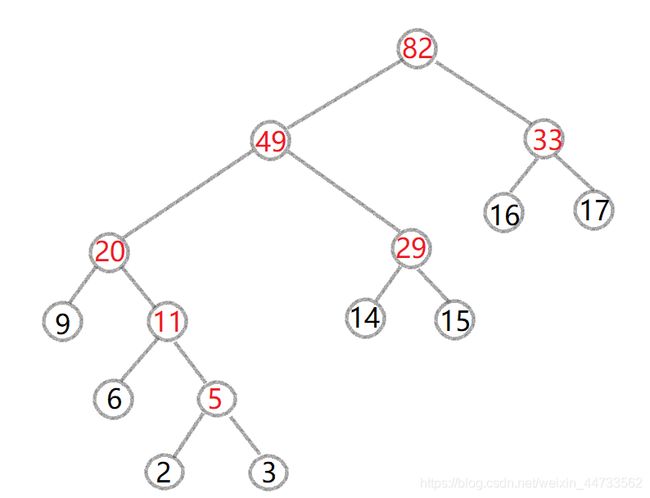
举个例子:现在有 权值为2,3,6,9,14,15,16,17的八个结点,构造出一棵哈夫曼树
(1).选出最小的两个2,3,构造一棵二叉树,获得新的根节点5,删除集合中的2,3,添加5进去
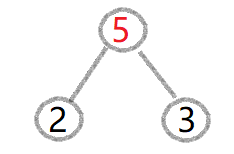
(2).此时集合为{5,6,9,14,15,16,17}依然从中选取两个最小的5与6,构造新的二叉树,获得新的根节点11,删除集合中的5与6
添加11进去。
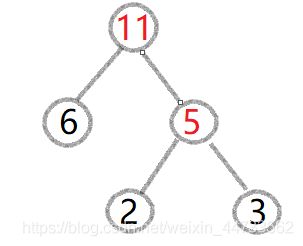
(3).此时集合为{9,11,14,15,16,17}依然从中选取两个最小的9与11,构造新的二叉树,获得新的根节点20,删除集合中的9与11
添加20进去。

(4).此时集合为{14,15,16,17,20}依然从中选取两个最小的14与15,构造新的二叉树,获得新的根节点29,删除集合中的14与15
添加29进去。
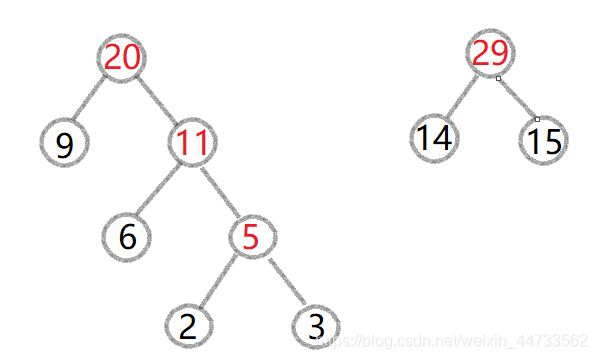
(5).此时集合为{16,17,20,29}依然从中选取两个最小的16与17,构造新的二叉树,获得新的根节点33,删除集合中的16与17
添加33进去。

(6).此时集合为{20,29,33}依然从中选取两个最小的20与29,构造新的二叉树,获得新的根节点49,删除集合中的20与29
添加49进去。
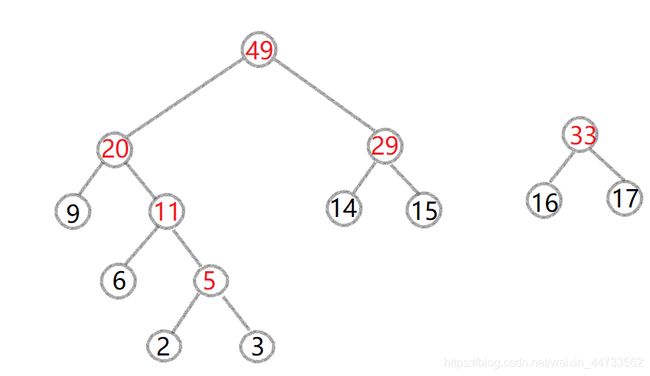
(7).此时集合为{33,49}依然从中选取两个最小的33与49,构造新的二叉树,获得新的根节点82,删除集合中的33与49
添加82进去。此时一棵哈夫曼树就构造完成了
二.哈夫曼编码
上面我们讲了哈夫曼树的构造方法,由此我们引出哈夫曼树最广泛的应用之一:哈夫曼编码
哈夫曼编码(Huffman Coding),是一种编码方式,哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码
该定义中的“字符出现概率”与“异字头”是哈夫曼编码的核心
1.使用哈夫曼编码的原因
在传送电文时,希望总长尽可能的短。如果对每个字符设计长度不等的编码,且让电文中出现次数较多的字符采用尽可能短的编码,则传送电文的总长度便可减少。
假如设计ABCD的编码分别为0、00、1、01,则如果传送报文ABACCDA,那么可转换为总长为9的字符串‘000011010’。但是这样的电文无法翻译,例如传送过去的字符串中前4个字符的字符串为“0000”就可有多种译法,或是‘AAAA’或是‘ABA’,也可以是‘BB’等。这样翻译出来的结果不唯一,故我们要采用哈夫曼编码的方式去编码
2.哈夫曼编码的方式
由上文可知,若要设计长短不等的编码,则必须是任一个字符的编码都不是另一个字符的编码的前缀,这种编码称为前缀编码。
且要保证电文的总长最短,所以出现高频率的字符的编码短,低频率的字符的编码长
根据以上两点,我们采用哈夫曼树来构造哈夫曼编码。
把字符出现的概率看成字符的权值去构造一棵哈夫曼树,且树中的左分支表示字符‘0’,右分支表示字符‘1’,则可以从根节点到叶子结点的路径上分支字符组成的字符串作为该叶子结点字符的编码。
例如:现在有A,B,C,D,E,F这几个字符,他们出现的概率分别是2%,17%,34%,21%,16%,10%,则他们构造出的哈夫曼树如下图
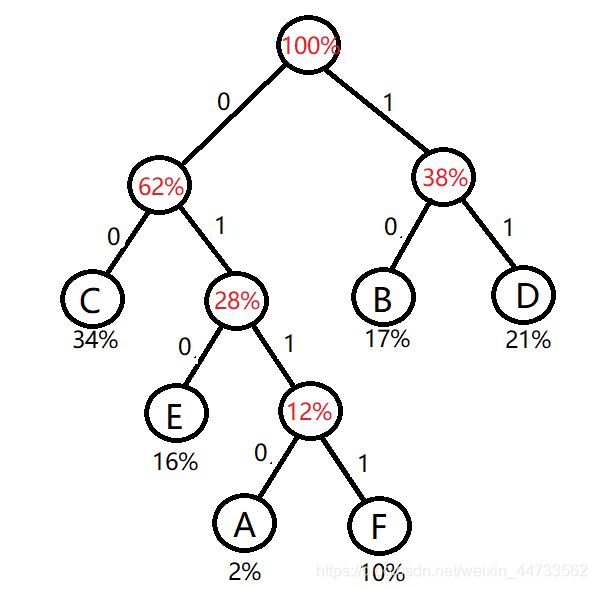
小编需要鼓励!!画图不易,且行且珍惜哦嘿嘿
由图可知各个字符的哈夫曼编码为
A:0110
B:10
C:00
D:11
E:010
F:0111
神奇不,任一个字符的编码都不是别的字符的前缀。现在我们的盟友发过来一串电报1011100110101110101111010000
聪明的你能翻译出来么?我相信你一定可以的,就当是课堂小作业喽!