二值化方法

一、全局阈值法

1.固定阈值方法

该方法是对于输入图像中的所有像素点统一使用同一个固定阈值。其基本思想如下:

其中，T为全局阈值。

 

缺点:很难为不同的输入图像确定最佳阈值。

 

2.Otsu算法

Otsu算法又称最大类间方差法

先明确两个概念:

(1)均值

 

(2)方差

 

图像的阈值化处理，就是将图像分为两个部分，高于阈值的部分，和小于阈值的部分。（暂不考虑多阈值的情况）。那么，如果将图像的每一个像素点的强度作为一个数据集合中的单元，那么，阈值化就相当于是一个二分类的问题。

 

我们假设，大于阈值的类为S1，维度为n1（不考虑秩的问题，实际上就是像素个数），均值为m1；小于阈值的类记为S2，维度为n2，均值为m2。根据前面概率的知识，理想的情况下，对于每一个类，其类内方差应该是很小的。

 

当然了，考虑每一个类是可行的。但是，我们又可以换个思路，全局上来考虑呢？

 

假设整个图像的均值为m，我们假设就只有两个数据，m1,m2，考虑着两个数据的离散程度，同样可以用上面的方差公式。这里看起来有点怪怪的，暂且这样来理解吧。也就是说，方差越大，这两个类也就越离散，分的越开。就像吵架一样，吵得声音越大，说明分歧越大，越严重。

 

所以，我们求这个阈值时，就希望，在内部是很团结的，就是在阈值分割后，两个类中，每一个类都是很和谐的。但是，相互之间又非常的受不了对方，离的越远越好。那么，找到这样的阈值，就十分开心了。

 

缺点:当目标物体与背景大小比例悬殊或灰度级接近，导致直方图呈现三峰或双峰峰值差距极大时，Otsu算法往往得不到满意的结果

 

 

二、局部阈值法

 

1.自适应阈值算法

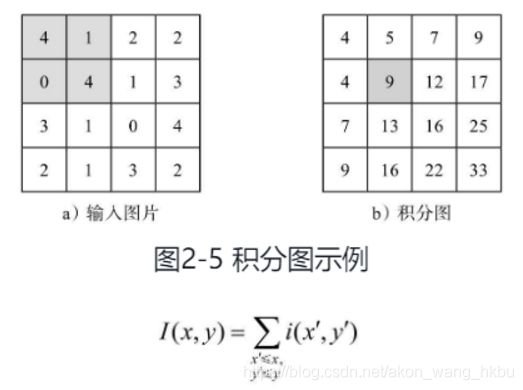
自适应阈值算法[2]用到了积分图（Integral Image）的概念，它是一个快速且有效地对网格的矩形子区域计算和的算法。积分图中任意一点 (x, y) 的值是从图左上角到该点形成的矩形区域内所有值之和。图2-5b中的灰色部分为图2-5a中灰色矩阵内值的加和：

 

自适应阈值算法的主要思想是以一个像素点为中心设置大小为 s×s 的滑窗，滑窗扫过整张图像，每次扫描均对窗口内的像素求均值并将均值作为局部阈值。若窗口中的某一像素值低于局部阈值t/100，赋值为0；高于局部阈值t/100，赋值为255。因为涉及多次对有重叠的窗口进行加和计算，因此积分图的使用可以有效地降低复杂度和操作次数。为了计算积分图，我们在每个位置存储其左边和上方所有 f(x, y) 值的总和，这一步骤会在线性时间内完成：

                                                                   I(x, y)= f(x, y)+I(x-1, y)+I(x, y-1)-I(x-1, y-1)

一旦得到积分图，对于任意从左上角 (x1y1, ) 到右下角(x2y2, ) 的矩形内（如图2-6所示）的数值总和均可以使用式（2.2）计算：

 

流程共扫描全图两次，第一次扫描获得积分图intImg，第二次扫描根据式（2.2）计算每次扫描窗口内像素值的平均值的（100-t）/100，并将计算结果作为局部阈值。若窗口内某一像素点的值乘以窗口大小大于该阈值，则对应输出255，反之则输出0。

 

2. Niblack算法

Niblack算法同样是根据窗口内的像素值来计算局部阈值的，不同之处在于它不仅考虑到区域内像素点的均值和方差，还考虑到用一个事先设定的修正系数 k 来决定影响程度。

                                                                                  T(x, y)=m(x, y)+ks(x, y)

其中，T(x, y) 为阈值，m(x, y)、s(x, y) 分别代表均值与方差。与 m(x, y) 相近的像素点被判定为背景，反之则判定为前景，而相近的程度则由标准差和修正系数来决定，这样做可以保证算法的灵活性。

 

缺点:Niblack算法的缺陷一方面在于 r × r 的滑窗会导致在边界区域(r-1)/2的像素范围内无法求取阈值；另一方面在于如果 r×r 滑窗内全部是背景，那么该算法必然会使一部分像素点成为前景，形成伪噪声。因此，r的选择非常关键，若窗口太小，则不能有效地抑制噪声；若窗口太大，则会导致细节丢失。

 

3. Sauvola算法

Sauvola算法是针对文档二值化处理，在Niblack算法基础上的改进：

 

 

其中，R是标准方差的动态范围，若当前输入图像是8位灰度图像，则 R=128。Sauvola算法在处理光线不均匀或染色图像时，比Niblack算法拥有更好的表现，因为式（2.3）以自适应的方式放大了标准差s的作用。假设我们要处理一份浅色但有污渍的文档，那么乘以m系数会降低背景区域阈值的范围，这可以有效地减少染色、污渍等带来的影响。表2-1展示了Sauvola与Niblack算法在处理染色文档时的效果差异。

三、其他方法

对于灰度图而言，腐蚀和膨胀运算都类似于卷积操作——将结构元素在原图上平移，而结构元素上的原点就相当于卷积核的核中心。首先我们约定，将结构元素覆盖住的原图区域记为P。

1.腐蚀

如图2-10所示，腐蚀运算即在平移过程中依次计算 P 和 结构元素的差矩阵，并将该矩阵中的最小值赋给原点对应的原图位置.

 

2.膨胀

如图2-11所示，膨胀运算则是计算 P 和结构元素的和矩阵，并将该矩阵中的最大值赋给原点对应的原图位置。

 

3.开运算

开运算是先腐蚀后膨胀,开运算可以使图像的轮廓变得光滑，断开狭窄的连接并消除细毛刺

 

4.闭运算

闭运算是先膨胀后腐蚀.闭运算同样可以平滑轮廓，但其具体作用是排除小型空洞，弥合狭窄的间断点、沟壑以及填补断裂的轮廓线。