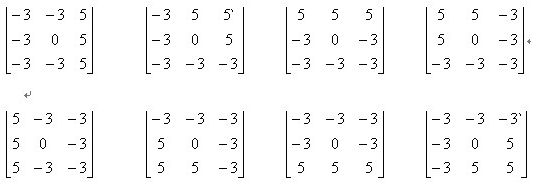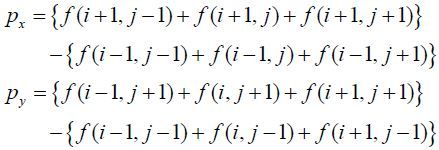OpenCV3学习（6.1）——边缘检测---Canny,Sobel,Prewitt,Robert,Laplace,LOG,DOG算子

      图像边缘信息主要集中在高频段，通常说图像锐化或检测边缘，实质就是高频滤波。我们知道微分运算是求信号的变化率，具有加强高频分量的作用。在空域运算中来说，对图像的锐化就是计算微分。由于数字图像的离散信号，微分运算就变成计算差分或梯度。图像处理中有多种边缘检测（梯度）算子，常用的包括普通一阶差分，Robert算子（交叉差分），Sobel算子等等，是基于寻找梯度强度。拉普拉斯算子（二阶差分）是基于过零点检测。通过计算梯度，设置阀值，得到边缘图像。

边缘检测的一般步骤：

1. 滤波——消除噪声，边缘检测的算法主要是基于图像强度的一阶和二阶导数，但导数通常对噪声很敏感，因此必须采用滤波器来改善与噪声有关的边缘检测器的性能。常见的滤波方法主要有高斯滤波，即采用离散化的高斯函数产生一组归一化的高斯核（具体见“高斯滤波原理及其编程离散化实现方法”一文），然后基于高斯核函数对图像灰度矩阵的每一点进行加权求和
2. 增强——使边界轮廓更加明显。增强边缘的基础是确定图像各点邻域强度的变化值。增强算法可以将图像灰度点邻域强度值有显著变化的点凸显出来。在具体编程实现时，可通过计算梯度幅值来确定。
3. 检测——选出边缘点。经过增强的图像，往往邻域中有很多点的梯度值比较大，而在特定的应用中，这些点并不是我们要找的边缘点，所以应该采用某种方法来对这些点进行取舍。实际工程中，常用的方法是通过阈值化方法来检测。

1、Canny算法

Canny边缘检测算法被很多人推崇为当今最优秀的边缘检测算法，opencv中提供了Canny函数：

void Canny( InputArray image, OutputArray edges,
                         double threshold1, double threshold2,
                         int apertureSize=3, bool L2gradient=false );

第一个参数，InputArray类型的image，输入图像，即源图像，填Mat类的对象即可，且需为单通道8位图像。
第二个参数，OutputArray类型的edges，输出的边缘图，需要和源图片有一样的尺寸和类型。
第三个参数，double类型的threshold1，第一个滞后性阈值。
第四个参数，double类型的threshold2，第二个滞后性阈值。
第五个参数，int类型的apertureSize，表示应用Sobel算子的孔径大小，其有默认值3。
第六个参数，bool类型的L2gradient，一个计算图像梯度幅值的标识，有默认值false。
函数中阈值1和阈值2两者的小者用于边缘连接，而大者用来控制强边缘的初始段，推荐的高低阈值比在2:1到3:1之间

1.1 canny算子简介

         Canny边缘检测算子是John F.Canny于 1986 年开发出来的一个多级边缘检测算法。更为重要的是 Canny 创立了边缘检测计算理论（Computational theory ofedge detection），解释了这项技术是如何工作的。Canny边缘检测算法以Canny的名字命名，被很多人推崇为当今最优的边缘检测的算法。其中，Canny 的目标是找到一个最优的边缘检测算法，让我们看一下最优边缘检测的三个主要评价标准:

1.低错误率: 标识出尽可能多的实际边缘，同时尽可能的减少噪声产生的误报。

2.高定位性: 标识出的边缘要与图像中的实际边缘尽可能接近。

3.最小响应: 图像中的边缘只能标识一次，并且可能存在的图像噪声不应标识为边缘。

       为了满足这些要求 Canny 使用了变分法，这是一种寻找满足特定功能的函数的方法。最优检测使用四个指数函数项的和表示，但是它非常近似于高斯函数的一阶导数。

1.2 Canny 边缘检测的步骤

1.消除噪声。 一般情况下，使用高斯平滑滤波器卷积降噪。 如下显示了一个 size = 5 的高斯内核示例:

                                      

 

2.（这一步就是用差分运算求梯度，至于用soble，还是Robert，都行，任选）计算梯度幅值和方向。图像的边缘可以指向不同方向，因此经典Canny算法用了4个梯度算子来分别计算水平，垂直和对角线方向的梯度。但是通常都不用四个梯度算子来分别计算四个方向。常用的边缘差分算子（如Rober，Prewitt，Sobel）计算水平和垂直方向的差分Gx和Gy。这样就可以如下计算梯度模和方向。此处，选择Sobel算子计算梯度。

     canny可用方向算子Kirsch（8个3*3模板），Nevitia （12个5*5模板），这两个算子是利用多个方向的子模板进行分别计算，最后取幅值最大的那个为最终边缘幅值，方向即最大幅值对应的那个方向。Kirsch如下：

                         

也可以用近似方法求梯度方向，如下：

Ⅰ.运用一对卷积阵列 (分别作用于 x 和 y 方向):

                                

Ⅱ.使用下列公式计算梯度幅值和方向:

                                                               

          梯度方向近似到四个可能角度之一(一般为0, 45, 90, 135)

3.非极大值抑制。 这一步排除非边缘像素， 仅仅保留了一些细线条(候选边缘)。

4.滞后阈值。最后一步，Canny 使用了滞后阈值，滞后阈值需要两个阈值(高阈值和低阈值):

Ⅰ.如果某一像素位置的幅值超过 高阈值, 该像素被保留为边缘像素。

Ⅱ.如果某一像素位置的幅值小于 低阈值, 该像素被排除。

Ⅲ.如果某一像素位置的幅值在两个阈值之间,该像素仅仅在连接到一个高于 高阈值的像素时被保留。

对于Canny函数的使用，推荐的高低阈值比在2:1到3:1之间。from：https://www.cnblogs.com/mightycode/p/6394810.html

特点

     Canny方法不容易受噪声干扰，能够检测到真正的弱边缘。优点在于，使用两种不同的阈值分别检测强边缘和弱边缘，并且当弱边缘和强边缘相连时，才将弱边缘包含在输出图像中。

实例：

#include 
#include 
#include 
 

using namespace cv;

int main( )
{
	//载入原始图  
	Mat src = imread("1.jpg");  //工程目录下应该有一张名为1.jpg的素材图
	Mat src1=src.clone();

    Canny( src, src, 150, 100,3 );//canny可以直接用于彩色图片


	//转成灰度图，降噪，用canny，最后将得到的边缘作为掩码，拷贝原图到效果图上，得到彩色的边缘图
	Mat dst,edge,gray;
	dst.create( src1.size(), src1.type() );
	cvtColor( src1, gray, CV_BGR2GRAY );
	blur( gray, edge, Size(3,3) );	//先用使用 3x3内核来降噪
	Canny( edge, edge, 3, 9,3 );
	dst = Scalar::all(0); 
	//使用Canny算子输出的边缘图g_cannyDetectedEdges作为掩码，来将原图g_srcImage拷到目标图g_dstImage中
	src1.copyTo( dst, edge);
 
	imshow("Canny边缘检测", dst);  
	waitKey(0);  
	return 0; 
}

2、Sobel算法

     Sobel 算子是一个主要用作边缘检测的离散微分算子 (discrete differentiation operator)。 它Sobel算子结合了高斯平滑和微分求导，用来计算图像灰度函数的近似梯度。在图像的任何一点使用此算子，将会产生对应的梯度矢量或是其法矢量。函数原型：

void Sobel( InputArray src, OutputArray dst, int ddepth,
                         int dx, int dy, int ksize=3,
                         double scale=1, double delta=0,
                         int borderType=BORDER_DEFAULT );

 第一个参数，InputArray 类型的src，为输入图像，填Mat类型即可。

第二个参数，OutputArray类型的dst，即目标图像，函数的输出参数，需要和源图片有一样的尺寸和类型。

第三个参数，int类型的ddepth，输出图像的深度，支持如下src.depth()和ddepth的组合：

                  若src.depth() = CV_8U, 取ddepth =-1/CV_16S/CV_32F/CV_64F

                  若src.depth() = CV_16U/CV_16S, 取ddepth =-1/CV_32F/CV_64F

                  若src.depth() = CV_32F, 取ddepth =-1/CV_32F/CV_64F

                  若src.depth() = CV_64F, 取ddepth = -1/CV_64F

第四个参数，int类型dx，x 方向上的差分阶数。

第五个参数，int类型dy，y方向上的差分阶数。

第六个参数，int类型ksize，有默认值3，表示Sobel核的大小;必须取1，3，5或7。

第七个参数，double类型的scale，计算导数值时可选的缩放因子，默认值是1，表示默认情况下是没有应用缩放的。

第八个参数，double类型的delta，表示在结果存入目标图（第二个参数dst）之前可选的delta值，有默认值0。

第九个参数， int类型的borderType，我们的老朋友了（万年是最后一个参数），边界模式，默认值为BORDER_DEFAULT。一般不用理会。

一般情况下，都是用ksize x ksize内核来计算导数的。然而，有一种特殊情况——当ksize为1时，往往会使用3 x 1或者1 x 3的内核。且这种情况下，并没有进行高斯平滑操作。

2.1、sobel算子的计算过程

我们假设被作用图像为 I.然后进行如下的操作：

1.分别在x和y两个方向求导。

Ⅰ.水平变化: 将 I 与一个奇数大小的内核进行卷积。

                                                       

Ⅱ.垂直变化: 将: I 与一个奇数大小的内核进行卷积。

                                                    

2.在图像的每一点，结合以上两个结果求出近似梯度:

                                                              
                                                              

        有时 也可用下面更简单公式代替:

                               ，或者

如果梯度G大于某一阀值 则认为该点(x,y)为边缘点。

 补充说明：

    1.当内核大小为 3 时, 我们的Sobel内核可能产生比较明显的误差(毕竟，Sobel算子只是求取了导数的近似值而已)。 为解决这一问题，OpenCV提供了Scharr 函数，但该函数仅作用于大小为3的内核。该函数的运算与Sobel函数一样快，但结果却更加精确，其内核是这样的:

                                 

    2.因为Sobel算子结合了高斯平滑和分化（differentiation），因此结果会具有更多的抗噪性。大多数情况下，我们使用sobel函数时，取【xorder = 1，yorder = 0，ksize = 3】来计算图像X方向的导数，【xorder = 0，yorder = 1，ksize = 3】来计算图像y方向的导数。

计算图像X方向的导数，取【xorder= 1，yorder = 0，ksize = 3】情况对应的内核：
                                                                
而计算图像Y方向的导数，取【xorder= 0，yorder = 1，ksize = 3】对应的内核：

                                                             
特点：

    Sobel算子检测方法对灰度渐变和噪声较多的图像处理效果较好，sobel算子对边缘定位不是很准确，图像的边缘不止一个像素；当对精度要求不是很高时，是一种较为常用的边缘检测方法

实例：

#include   
#include

using namespace std;
using namespace cv;

int main()
{
    Mat img = imread("123.jpg");
    imshow("img", img);
    Mat grad_x, grad_y;
    Mat abs_grad_x, abs_grad_y, dst;

    //求x方向梯度
    Sobel(img, grad_x, CV_16S, 1, 0, 3, 1, 1,BORDER_DEFAULT);
    convertScaleAbs(grad_x, abs_grad_x);
    imshow("x方向soble", abs_grad_x);

    //求y方向梯度
    Sobel(img, grad_y,CV_16S,0, 1,3, 1, 1, BORDER_DEFAULT);
    convertScaleAbs(grad_y,abs_grad_y);
    imshow("y向soble", abs_grad_y);

    //合并梯度
    addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, dst);
    imshow("整体方向soble", dst);
    waitKey(0);
}

补充：

convertScaleAbs()用于实现对整个图像数组中的每一个元素，进行如下操作：
 该操作可实现图像增强等相关操作的快速运算，将图片转化成为8位（uchar无符号字符）图形进行显示，具体用法如下：

void cv::convertScaleAbs(
    cv::InputArray src, // 输入数组
    cv::OutputArray dst, // 输出数组
    double alpha = 1.0, // 乘数因子
    double beta = 0.0 // 偏移量
);

3、 Roberts算子

Robert算子是第一个边缘检测算子。是最初的算子。

                              

                                     

4、Prewitt 算子

     Prewitt边缘检测算子与soble基本相同，只是算子的权重不同。 Prewitt边缘检测算子使用两个有向算子(水平+垂直)，每一个逼近一个偏导数，这是一种类似计算偏微分估计值的方法，x，y两个方向的近似检测算子为：、

                                 

​      得出卷积模板为：

                                 

       记图像M，阀值T

                                 

5、scharr滤波器

     scharr一般称它为滤波器，而不是算子。上文我们已经讲到，它在OpenCV中主要是配合Sobel算子的运算而存在的,一个万年备胎。让我们直接来看看函数讲解吧。

void Scharr( InputArray src, OutputArray dst, int ddepth,
                          int dx, int dy, double scale=1, double delta=0,
                          int borderType=BORDER_DEFAULT );

使用Scharr滤波器运算符计算x或y方向的图像差分。其实它的参数变量和Sobel基本上是一样的，除了没有ksize核的大小。所以如下两者是等价的：

Scharr(src, dst, ddepth, dx, dy, scale,delta, borderType);  
 
Sobel(src, dst, ddepth, dx, dy, CV_SCHARR,scale, delta, borderType); 

---

二阶微分算子

6、Laplacian算法

       拉普拉斯算子是不依赖于边缘方向的二阶导数算子，它是一个标量而不是向量，具有旋转不变即各向同性的性质，所以不具有方向性。Laplacian 算子是n维欧几里德空间中的一个二阶微分算子，定义为梯度grad（f）的散度div=div(grad f)。因此如果f是二阶可微的实函数，则f的拉普拉斯算子定义为：

                                                   

为了更适合于数字图像处理，将该方程表示为离散形式：

                              

二阶微分算子，求图像灰度变化导数的导数，对图像中灰度变化强烈的地方很敏感，从而可以突出图像的纹理结构。

推导：

       f(x,y)对x右侧的一阶偏导(因为相邻点像素距离差为1，所以分母为1略去)：
                                             

       f(x,y)对x左侧的一阶偏导（同上）：
                                         

       f(x,y)对x的二阶偏导(右侧一阶减左侧一阶，分母仍然是1略去)： 

     f(x,y)对y的二阶偏导（同上）：

      根据图像处理的原理我们知道，二阶导数可以用来进行检测边缘 。 因为图像是 “二维”, 我们需要在两个方向进行求导。使用Laplacian算子将会使求导过程变得简单。

需要点破的是，由于 Laplacian使用了图像梯度，它内部的代码其实是调用了Sobel 算子的。

小tips：让一幅图像减去它的Laplacian可以增强对比度。

特点：

     Laplacian算子法对噪声比较敏感，所以很少用该算子检测边缘，而是用来判断边缘像素视为与图像的明区还是暗区。拉普拉斯高斯算子是一种二阶导数算子，将在边缘处产生一个陡峭的零交叉, Laplacian算子是各向同性的，即与坐标轴方向无关，坐标轴旋转后梯度结果不变，能对任何走向的界线和线条进行锐化，无方向性。这是拉普拉斯算子区别于其他算法的最大优点。

void Laplacian( InputArray src, OutputArray dst, int ddepth,
                             int ksize=1, double scale=1, double delta=0,
                             int borderType=BORDER_DEFAULT );

第一个参数，InputArray类型的image，输入图像，即源图像，填Mat类的对象即可，且需为单通道8位图像。

第二个参数，OutputArray类型的edges，输出的边缘图，需要和源图片有一样的尺寸和通道数。

第三个参数，int类型的ddept，目标图像的深度。

第四个参数，int类型的ksize，用于计算二阶导数的滤波器的孔径尺寸，大小必须为正奇数，且有默认值1。

第五个参数，double类型的scale，计算拉普拉斯值的时候可选的比例因子，有默认值1。

第六个参数，double类型的delta，表示在结果存入目标图（第二个参数dst）之前可选的delta值，有默认值0。

第七个参数， int类型的borderType，边界模式，默认值为BORDER_DEFAULT。

    Laplacian( )函数其实主要是利用sobel算子的运算。它通过加上sobel算子运算出的图像x方向和y方向上的导数，来得到我们载入图像的拉普拉斯变换结果。

其中，sobel算子（ksize>1）如下：

                                            

而当ksize=1时，Laplacian()函数采用以下3x3的孔径：

                                                               

实例：

#include   
#include

using namespace std;
using namespace cv;

int main()
{
    Mat img = imread("lol3.jpg");
    imshow("原始图", img);
    Mat gray, dst,abs_dst;
    //高斯滤波消除噪声
    GaussianBlur(img, img, Size(3, 3), 0, 0, BORDER_DEFAULT);
    cvtColor(img, gray, COLOR_RGB2GRAY);
    Laplacian(gray, dst, CV_16S, 3, 1, 0, BORDER_DEFAULT);
    //计算绝对值，并将结果转为8位
    convertScaleAbs(dst, abs_dst);
    imshow("laplace", abs_dst);
    waitKey(0);

}

7、高斯拉普拉斯算子(LoG, Laplacian of Gaussian)

1980年，Marr和Hildreth提出将Laplace算子与高斯低通滤波相结合，提出了LOG（Laplace of Guassian）算子。

步骤如下：

1、对于图像I(x,y) ，首先通过尺度为的高斯平滑
                                      

2、再使用Laplace算子检测边缘

                    

                               
微分算子与卷积算子的次序可以交换， 所以高斯拉普拉斯算子等价于先对高斯函数求二阶导，再与原图进行卷积 ： 

 LOG算子如下：
                          
    根据sigma的不同以及3sigma原则可以建立不同的模板，sigma是一个尺度参数，在图像处理中引入尺度以及建立多尺度空间是一个重要的突破，sigma越大，图像越模糊滤除噪声效果越好，sigma越小，效果相反。

常用模板如下：

                                                         

边缘检测步骤如下：

1.对图像先进行高斯滤波（G × f），再进行Laplace算子运算Δ（G × f）；

2.保留一阶导数峰值的位置，从中寻找Laplace过零点；

3.对过零点的精确位置进行插值估计。

                  

from：https://blog.csdn.net/u014485485/article/details/78364573

8、DOG算子

由数学上的关系，我们可以简化LOG的计算——这便是DOG算子。

我们定义DOG算子：

                      
当我们用DOG算子代替LOG算子与图像卷积的时候：

     
这样，我们只要对图像进行两次高斯平滑再将结果相减就可以近似得到LOG作用于图像的效果了！

 各边缘检测算子对比

      

from：https://blog.csdn.net/poem_qianmo/article/details/25560901  

from：https://blog.csdn.net/tigerda/article/details/61192943