《OpenCv视觉之眼》Python图像处理二十二:Opencv图像处理实战五之图像中直线和圆的检测原理及实现

本专栏主要介绍如果通过OpenCv-Python进行图像处理，通过原理理解OpenCv-Python的函数处理原型，在具体情况中，针对不同的图像进行不同等级的、不同方法的处理，以达到对图像进行去噪、锐化等一系列的操作。同时，希望观看本专栏的小伙伴可以理解到OpenCv进行图像处理的强大哦，如有转载，请注明出处(原文链接和作者署名)，感谢各位小伙伴啦！

前文参考：
《OpenCv视觉之眼》Python图像处理一 :Opencv-python的简介及Python环境搭建
《OpenCv视觉之眼》Python图像处理二 :Opencv图像读取、显示、保存基本函数原型及使用
《OpenCv视觉之眼》Python图像处理三 :Opencv图像属性、ROI区域获取及通道处理
《OpenCv视觉之眼》Python图像处理四 :Opencv图像灰度处理的四种方法及原理
《OpenCv视觉之眼》Python图像处理五 :Opencv图像去噪处理之均值滤波、方框滤波、中值滤波和高斯滤波
《OpenCv视觉之眼》Python图像处理六 :Opencv图像傅里叶变换和傅里叶逆变换原理及实现
《OpenCv视觉之眼》Python图像处理七 :Opencv图像处理之高通滤波和低通滤波原理及构造
《OpenCv视觉之眼》Python图像处理八 :Opencv图像处理之图像阈值化处理原理及函数
《OpenCv视觉之眼》Python图像处理九 :Opencv图像形态学处理之图像腐蚀与膨胀原理及方法
《OpenCv视觉之眼》Python图像处理十 :Opencv图像形态学处理之开运算、闭运算和梯度运算原理及方法
《OpenCv视觉之眼》Python图像处理十一 :Opencv图像形态学处理之顶帽运算与黑帽运算
《OpenCv视觉之眼》Python图像处理十二 :Opencv图像轮廓提取之基于一阶导数的Roberts算法、Prewitt算法及Sobel算法
《OpenCv视觉之眼》Python图像处理十三 :Opencv图像轮廓提取之基于二阶导数的Laplacian算法和LOG算法
《OpenCv视觉之眼》Python图像处理十四 :Opencv图像轮廓提取之Scharr算法和Canny算法
《OpenCv视觉之眼》Python图像处理十五 :Opencv图像处理之图像缩放、旋转和平移原理及实现
《OpenCv视觉之眼》Python图像处理十六:Opencv项目实战之图像中的硬币检测
《OpenCv视觉之眼》Python图像处理十七:Opencv图像处理实战二之图像中的物体识别并截取
《OpenCv视觉之眼》Python图像处理十八:Opencv图像处理实战三之基于OpenCV训练模型的AI人脸检测
《OpenCv视觉之眼》Python图像处理十九:Opencv图像处理实战四之通过OpenCV进行人脸口罩模型训练并进行口罩检测
《OpenCv视觉之眼》Python图像处理二十:Opencv图像美化处理之图像流年、光照、浮雕、素描、怀旧、滤镜、毛玻璃、油漆特效处理
《OpenCv视觉之眼》Python图像处理二十一:Opencv图像处理之图像线性变换和非线性变换的方法及原理

上次博客介绍了图像处理中的线性变换和非线性变换的原理及方法，对于图像的线性和非线性变换，在现实生活中的应用是比较广泛的，因此是比较重要的，例如常用的医学、破案、图像曝光处理等等，都是通过图像的线性或者是非线性变换处理后得到的结果，需要重点掌握。

本次博客，林君学长将带大家了解图像中直线和源的检测原理及实现方法，OpenCV在针对图像中直线和圆的检测都是通过霍夫空间变换实现的，在霍夫空间的基础上，实现对图像中直线和圆的检测，需要理解的是，在笛卡尔坐标系中的点，在霍夫空间中就是一条直线；而在笛卡尔坐标系中的直线，在霍夫空间中就是一个点，本次博客，主要带大家介绍霍夫空间中直线和圆的检测原理，一起学习吧！

OpenCV图像处理实战五：图像中直线和圆的检测原理及实现

---

霍夫变换是一种特征检测(feature extraction)，被广泛应用在图像分析(image analysis)、计算机视觉(computer vision)以及数位影像处理(digital image processing)。霍夫变换是用来辨别找出物件中的特征，例如：线条。他的算法流程大致如下，给定一个物件、要辨别的形状的种类，算法会在参数空间(parameter space)中执行投票来决定物体的形状，而这是由累加空间(accumulator space)里的局部最大值(local maximum)来决定。

现在广泛使用的霍夫变换是由RichardDuda和PeterHart在公元1972年发明，并称之为广义霍夫变换(generalizedHoughtransform)，广义霍夫变换和更早前1962年的PaulHough的专利有关。经典的霍夫变换是侦测图片中的直线，之后，霍夫变换不仅能识别直线，也能够识别任何形状，常见的有圆形、椭圆形。1981年，因为DanaH.Ballard的一篇期刊论文"Generalizing
the Hough transform to detect arbitrary shapes"，让霍夫变换开始流行于计算机视觉界

一、霍夫直线检测

霍夫直线检测原理分为以下几个步骤：

• 1、以图像中的每个像素为点，建立笛卡尔坐标系，然后将笛卡尔坐标系中的点映射到霍夫空间(极坐标系)
• 2、对$\theta$进行离散化处理
• 3、统计($r$,$\theta$)出现的次数
• 4、取局部极大值，设定阈值，过滤干扰直线
• 5、绘制直线、标定角点

1、霍夫直线检测原理

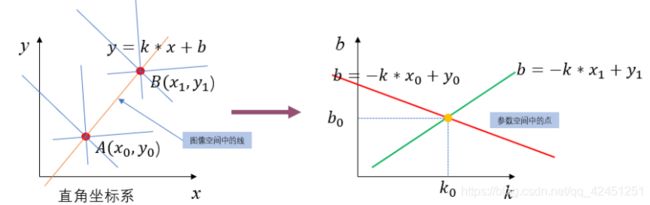
1）、图像空间(笛卡尔坐标系)中的直线与参数空间(霍夫空间)中的点一一对应
假设图像中有一条直线，$y=kx+b$，x和y分别表示自变量和因变量；k和b分别表示直线的斜率和截距；那么映射到霍夫空间中去的映射关系为$b=-xk+y$,这时候，-x和y是表示霍夫空间中这这条直线的斜率和截距，而k和b分别表示自变量和因变量，由于图像空间中的直线k和b是确定的，因此，在霍夫空间中，(k,b)就是一个点，如下所示

2）、图像空间(笛卡尔坐标系)中的点与参数空间(霍夫空间)中的直线一一对应
现在，我们假设图像空间中有一个点($x_1,y_1$)，当我们映射到霍夫空间的时候，通过霍夫变换公式$b=-x_{1}k+y_1$得到的就是一条直线，因为b和k我们未知，已知点($x_1,y_1$)，就可以求得很多个b和k的组合，而这些组合到一起就是一条直线，如下所示：

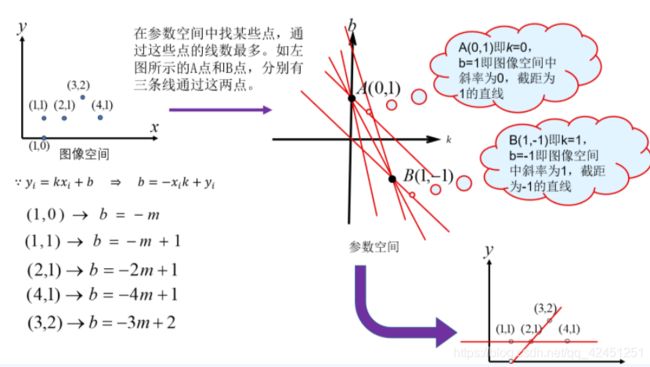
3）、我们可以知道，在图像空间也就是笛卡尔坐标中，两个点可以确定一条直线，那么映射到霍夫空间中变为两条直线相交于一个点，如下所示：

多个点的映射如下：

提示：直角坐标属于特殊的笛卡尔坐标，是笛卡尔坐标中的一种
4）、那么反过来讲，如果霍夫空间中有多条直线相较于一点，在笛卡尔坐标中表示什么呢？是不是就表示这条直线由多少个点组成呢？答案是肯定的，如果霍夫空间的多条直线相较于一个点，那么我们只需要统计这个点有多少条直线，然后在笛卡尔坐标系中就可以与这些直线对应的点的坐标；霍夫空间多少条直线交于一点，笛卡尔坐标中就有多少个点在同一条直线上，也就是共线，如下所示：

以上就是霍夫空间进行直线检测的原理，统计霍夫空间中局部区域相交直线最多的点，而这些相交的直线的条数，就是图像空间中共线点的个数，找出这些共线的点，就可以在图像中确定这条直线；需要注意的是，在霍夫空间中首先需要找到这个直线相交最多的点；然后找出相交直线的其中两条可以确定直线，找出所有相交的直线通就可以确定这条线段

5）、这时候我们会发现，如果在笛卡尔坐标系中有特殊的直线例如x=c上面的点，，在霍夫空间中映射出来就没有交点，这样通过霍夫空间进行检测笛卡尔坐标中的直线就不会成功如下所示：

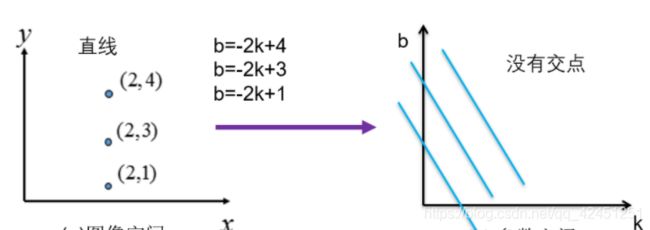
因此，我们需要引入极坐标，通过极坐标($r$,$\theta$)的方式代替之前的$b=-xk+y$的霍夫空间映射的方式；现在我们就用笛卡尔坐标系表示图像空间而用极坐标系表示霍夫空间，笛卡尔坐标系中的点转换到极坐标系中就是一条曲线，转换公式如下：
$$r=xcos\theta +ysin\theta$$
具体转换过程如下图所示：

这时候，我们可以发现，在笛卡尔坐标系中的特殊直线x=c的垂线，在极坐标系中就用$r=xcos\theta +ysin\theta =x=c$来表示；转换之后的极坐标系的霍夫空间与原来的笛卡尔坐标系的霍夫空间对比如下：

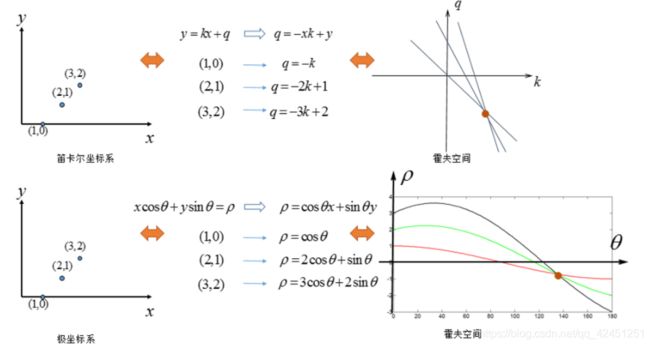
6）、上面我们可以知道，极坐标上的每个点(r,θ)都对应了笛卡尔坐标系中的一条直线，或者说图像空间的一个点在霍夫空间中就对应为一条曲线。霍夫空间采用极坐标系，这样就可以在霍夫空间表示图像空间中的所有直线了，如下：

以上就是霍夫直线检测的具体原理，比较抽象，抽象的点在于需要在笛卡尔坐标和极坐标相互理解转换，理解在笛卡尔坐标中的点在极坐标中表示一条直线，而在极坐标系中的点，在原图像中就是一条直线！而对于图像来说，每一个像素格都代表一个笛卡尔系中点，通过映射在极坐标系中，找到局部区域直线相交最多的那个点就ok！

2、霍夫直线检测实现

1）、OpenCV官方，提供了霍夫直线检测的库函数，包括cv2.HoughLines()和cv2.HoughLinesP()函数，区别就是cv2.HoughLines()函数检测出来的是一条直线，而cv2.HoughLinesP()函数检测出来的是一条线段，这里我们直接使用cv2.HoughLinesP()函数进行直线检测，函数原型如下：
line=cv2.HoughLinesP(image, rho, theta, threshold, minLineLength=None, maxLineGap=None)

• image： 必须是二值图像，推荐使用canny边缘检测的结果图像
• rho: 线段以像素为单位的距离精度，double类型的，推荐用1.0
• theta： 线段以弧度为单位的角度精度，推荐用numpy.pi/180
• threshod: 累加平面的阈值参数，int类型，超过设定阈值才被检测出线段，值越大，基本上意味着检出的线段越长，检出的线段个数越少。根据情况推荐先用100试试
• line：存放检测出来的线段起始点和终止点的数组，二维数组维度为多少条直线和直线的起始点和终止点
• minLineLength：线段以像素为单位的最小长度，根据应用场景设置
• maxLineGap：同一方向上两条线段判定为一条线段的最大允许间隔（断裂），超过了设定值，则把两条线段当成一条线段，值越大，允许线段上的断裂越大，越有可能检出潜在的直线段

2）、完整代码如下所示：

'''
    霍夫直线检测
'''
def hoffline(img):
     # 获取图像的长和宽
    h, w = img.shape[:2] 
      # 进行低通滤波,进行噪声点的排除
    image = cv2.blur(img, (5, 5))
    #对图像进行泛洪处理
    mask = np.zeros((h + 2, w + 2), np.uint8)  # 进行图像填充
    cv2.floodFill(image, mask, (w - 1, h - 1), (255, 255, 255), (2, 2, 2), (3, 3, 3), 8)
    # 图片灰度化处理
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    # 通过中值滤波对图像进行噪声过滤
    blurred = cv2.medianBlur(gray, 5)
    # 对图像进行二值处理Sobel算子
    ret, Binary = cv2.threshold(blurred, 127, 255, cv2.THRESH_BINARY)
    # Canny算子提取轮廓边缘
    Canny = cv2.Canny(Binary, 50, 150, 3)
    # 进行概率霍夫变换(直线检测)
    lines = cv2.HoughLinesP(Canny, 1, np.pi/180,20, minLineLength=10, maxLineGap=10)
    for line in lines:
        x1, y1, x2, y2 = line[0]
        # 将得到的直线在原图上面画出
        hough = cv2.line(img, (x1, y1), (x2, y2), (0, 255, 0), 1)
    return hough
#导入函数库
import cv2
import numpy as np
#np.set_printoptions(threshold=np.inf)  #打印数组中的全部内容
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #显示中文
#读取图像
img=cv2.imread("house.jpg")
#调用霍夫直线检测函数进行图像直线检测
hoffline=hoffline(img)#传递尺度比较常数0.00000005和伽玛值4
#图像显示
cv2.imshow("hoffline",hoffline)
#等待显示，键值结束
cv2.waitKey(0)

3）、最后，给出自己通过原理编写的霍夫直线检测python代码，由于运算量巨大，建议挑选尺寸小的图像，然后直线阈值尽量设置大一点，完整代码如下所示：

import cv2
import numpy as np
import matplotlib.pyplot as plt
#得到多点组成的线段
def coordinate(x17,x27):
    x1=np.array([])
    x2=np.array([])
    c2=np.array([])
    c1=[]
    for k in range(len(x17)):
        x1=x17[k]
        x2=x27[k]
        key_points = []
        for i in range(len(x1)-1):
            for j in range(i+1,len(x1)):
                c2=np.insert(c2,len(c2),(x1[i]-x1[j])**2+(x2[i]-x2[j])**2)
                key_points.append((i,j))
        h=np.argsort(c2)[-1]
        a,b=key_points[h]
        x11=x1[a]
        x21=x1[b]
        c,d=key_points[h]
        y11=x2[c]
        y21=x2[d]
        c1.append((x11,x21,y11,y21))
    return c1
img=cv2.imread("line.jpg")
img = cv2.resize(img, (240, 100), interpolation=cv2.INTER_CUBIC)
gray=cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
blurred=cv2.GaussianBlur(gray,(3,3),0,0,cv2.BORDER_DEFAULT)
Canny = cv2.Canny(blurred, 50, 150,3) 
x, y = Canny.shape[:2] #获取图像的长和宽
rho_max=int(np.sqrt(x**2+y**2))+1
AccArray = np.zeros([rho_max,180]).astype(np.uint8)	
x_points = []
y_points = []
keyX_points=[]
keyY_points=[]
thresholdValue=150                             #设定直线的最小值
for i in range(0,x):#将直线上的点取出（白点即像素值为255的点）
    for j in range(0,y):
        if Canny[i][j] == 255:
            for theta in range(180):
                rho = j * np.cos(theta/180*np.pi) + i * np.sin(theta/180*np.pi)
                #为了防止ρ值出现负数，将ρ值与ρ最大值的和的一半作为ρ的坐标值
                rho_int=int(rho/2+rho_max/2)
                #在极坐标中标识点，相同点累加
                AccArray[rho_int,theta]=AccArray[rho_int,theta]+1
                if AccArray[rho_int,theta]>=thresholdValue:
                    x_points.append(i)
                    y_points.append(j)
            keyX_points.append(x_points)
            keyY_points.append(y_points)
K=1 #存储数组计数器
case_accarray_rho=np.array([])
case_accarray_theta=np.array([])
for rho in range(rho_max):
	for theta in range(180):
		if AccArray[rho,theta]>=thresholdValue:
			case_accarray_rho=np.insert(case_accarray_rho,len(case_accarray_rho),rho)
			case_accarray_theta=np.insert(case_accarray_rho,len(case_accarray_rho),theta)
			K=K+1
print(K)
hough_img = np.zeros([x,y])
for i in range(0,x):#将直线上的点取出（白点即像素值为255的点）
    for j in range(0,y):
        if Canny[i][j] == 255:
            for theta in range(180):
            	rho = j * np.cos(theta/180*np.pi) + i * np.sin(theta/180*np.pi)
            	#为了防止ρ值出现负数，将ρ值与ρ最大值的和的一半作为ρ的坐标值
            	rho_int=int(rho/2+rho_max/2)
            	for a in range(K-1):
            		if rho_int==case_accarray_rho[a] and theta==case_accarray_theta[a]:
            			hough_img[i,j]=Canny[i,j]
cv2.imshow("hough_img",hough_img)
cv2.waitKey()
lines = coordinate(keyX_points,keyY_points)
for line in lines:
    x1, x2, y1, y2 = line
    #将得到的直线在原图上面画出
    hough=cv2.line(img, (x1, y1), (x2, y2), (0, 255, 0), 2)
cv2.imshow("hh",hough)
cv2.waitKey()

以上代码的运算量非常巨大，建议理解原理，掌握OpenCV霍夫直线检测的库函数的使用就行，运行以上代码需要花费大量的时间，同时，以上对于得到检测出来点组成的线段的函数需要进行优化，自行优化吧，林君学长的构思是将每个点相互求距离，找出距离最长的两个点，然后用画直线函数在原图上画出来，这种方法非常耗费时间，建议优化！

---

二、霍夫圆检测

霍夫圆变换的基本原理和霍夫线变换原理类似，只是点对应的二维极径、极角空间被三维的圆心和半径空间取代。在标准霍夫圆变换中，原图像的边缘图像的任意点对应的经过这个点的所有可能圆在三维空间用圆心和半径这三个参数来表示，其对应一条三维空间的曲线。对于多个边缘点，点越多，这些点对应的三维空间曲线交于一点的数量越多，那么他们经过的共同圆上的点就越多，类似的我们也就可以用同样的阈值的方法来判断一个圆是否被检测到，这就是标准霍夫圆变换的原理， 但也正是在三维空间的计算量大大增加的原因，标准霍夫圆变化很难被应用到实际中。

1、霍夫圆检测原理

1）、和霍夫直线检测一直，也需要将笛卡尔坐标系的点映射到极坐标系中，不同的是映射的方法不一样，直线检测是通过直线极坐标的映射得到，而圆检测则是根据圆的极坐标方程进行映射，如下：
在笛卡尔坐标系中圆的方程如下：
$$(x-a{)}^2+(y-b{)}^2=r^2$$
那么将其映射到极坐标中的原理如下图所示：

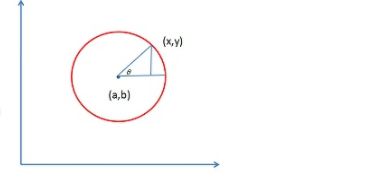
因此,笛卡尔坐标系转换为霍夫空间坐标系中就通过如下公式进行转换：
$$\begin{gathered} a=x-rcos\theta \\ b=y-rsin\theta \end{gathered}$$
2）、通过以上我们可以知道，在abr组成的三维坐标系中，一个点可以唯一确定一个圆；而在笛卡尔的xy坐标系中经过某一点的所有圆映射到abr坐标系中就是一条三维的曲线，如下所示：

经过xy坐标系中所有的非零像素点的所有圆就构成了abr坐标系中很多条三维的曲线；在xy坐标系中同一个圆上的所有点的圆方程是一样的，它们映射到abr坐标系中的是同一个点，所以在abr坐标系中该点就应该有圆的总像素$N_0$个曲线相交。通过判断abr中每一点的相交（累积）数量，大于一定阈值的点就认为是圆。

缺点：以上是标准霍夫圆变换实现算法，问题是它的累加面对一个三维的空间，意味着比霍夫直线变换需要更多的计算消耗。

3）、Opencv霍夫圆变换对标准霍夫圆变换做了运算上的优化。它采用的是“霍夫梯度法”。检测思路是去遍历累加所有非零点对应的圆心，对圆心进行考量。如何定位圆心呢？圆心一定是在圆上的每个点的模向量上，即在垂直于该点并且经过该点的切线的垂直线上，这些圆上的模向量的交点就是圆心；霍夫梯度法就是要去查找这些圆心，根据该“圆心”上模向量相交数量的多少，根据阈值进行最终的判断，如下所示：

注意：模向量即是圆上点的切线的垂直线

2、霍夫圆检测实现

1）、OpenCV官方也给出了霍夫圆检测的库函数cv2.HoughCircles(),该函数检测结果包括圆心和半径，然后通过画圆函数在图像进行圆的绘制；cv2.HoughCircles()函数原型如下所示：
circles=cv2.HoughCircles(image, method, dp, minDist, param1, param2, minRadius, maxRadius)

• circles：检测到的圆的圆心坐标和半径的数组，circles[0]为圆心的x坐标，circles[1]为圆心的y坐标，circles[2]为半径
• image：输入图像的轮廓图像
• method：检测方法,常用CV_HOUGH_GRADIENT
• dp：检测内侧圆心的累加器图像的分辨率于输入图像之比的倒数，如dp=1，累加器和输入图像具有相同的分辨率，如果dp=2，累计器便有输入图像一半那么大的宽度和高度
• minDist：两个圆之间圆心的最小距离
• param1：默认值100，它是method设置的检测方法的对应的参数，对当前唯一的方法霍夫梯度法cv2.HOUGH_GRADIENT，它表示传递给canny边缘检测算子的高阈值，而低阈值为高阈值的一半
• param2：默认值100，它是method设置的检测方法的对应的参数，对当前唯一的方法霍夫梯度法cv2.HOUGH_GRADIENT，它表示在检测阶段圆心的累加器阈值，它越小，就越可以检测到更多根本不存在的圆，而它越大的话，能通过检测的圆就更加接近完美的圆形了
• minRadius：默认值0，圆半径的最小值
• maxRadius：默认值0，圆半径的最大值

2）、霍夫圆检测OpenCV库函数实现完整代码如下：

'''
    霍夫圆检测
'''
#霍夫圆检测
def hoffcircle(img):
    # 获取图像的长和宽
    h, w = img.shape[:2]
    # 进行低通滤波,进行噪声点的排除
    image = cv2.blur(img, (5, 5)) 
    #泛洪处理
    mask = np.zeros((h + 2, w + 2), np.uint8)  # 进行图像填充
    cv2.floodFill(image, mask, (w - 1, h - 1), (255, 255, 255), (2, 2, 2), (3, 3, 3), 8)  # 进行泛洪处理
    # 灰度处理
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    #中值滤波去噪
    blurred = cv2.medianBlur(gray, 5)
    ret, Binary = cv2.threshold(blurred, 150, 255, cv2.THRESH_BINARY)
    #canny提取轮廓边缘
    Canny = cv2.Canny(Binary,50,150,3)
    # hough transform  规定检测的圆的最大最小半径，不能盲目的检测，否则浪费时间空间
    circle1 = cv2.HoughCircles(Binary, cv2.HOUGH_GRADIENT, 1, 45, param1=100, param2=30, minRadius=10,maxRadius=100)  # 把半径范围缩小点，检测内圆，瞳孔
    circles = circle1[0, :, :]  # 提取为二维
    circles = np.uint16(np.around(circles))  # 四舍五入，取整
    for i in circles[:]:
        cv2.circle(img, (i[0], i[1]), i[2], (0, 255, 0), 2)  # 画圆
        cv2.circle(img, (i[0], i[1]), 2, (0, 255, 0), 5)  # 画圆心
    return img
#导入函数库
import cv2
import numpy as np
#np.set_printoptions(threshold=np.inf)  #打印数组中的全部内容
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #显示中文
#读取图像
img=cv2.imread("coins6.jpg")
#调用霍夫圆检测函数进行图像直线检测
hoffcircle=hoffcircle(img)#传递尺度比较常数0.00000005和伽玛值4
#图像显示
cv2.imshow("hoffcircle",hoffcircle)
#等待显示，键值结束
cv2.waitKey(0)

对于通过霍夫圆检测原理编写自己的代码，林君学长自己并没有书写，因为直线都需要运行很久，圆检测就更不用说了，因此没有编写霍夫圆检测的原理代码哦，大家需要的话自己根据直线检测的代码编写圆检测的代码吧！

以上就是本次博客的全部内容，遇到问题的小伙伴记得留言评论，学长看到会为大家进行解答的，这个学长不太冷！

闭上眼睛，我看到了我的前途……

陈一月的又一天编程岁月^ _ ^