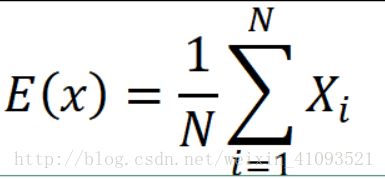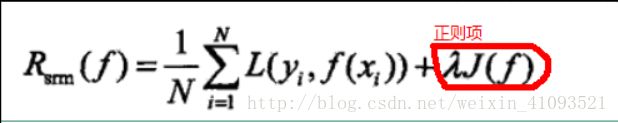统计学习方法
统计学习方法
统计学习是什么？
机器学习中所谓的学习就是从海量数据中学习到“经验”，再将这种“经验”应用与对未知数据的预测与分析！而这种思想的本质就是来自于统计学。可以所以说机器学习的本质就是统计学习方法，所以要研究机器学习的原理，就一定要从统计学习开始！
统计学习的分类
机器学习中的学习算法通常分为4类：
监督学习：数据为的数据都是有标签的数据，然后对数据集数据进行学习，通过学习到的方法对新数据进行预测的学习方式。
无监督学习：与监督学习相反的，无监督学习我们喂给她 的无标签的数据，对数据进行聚类等方式进行学习从而可以实现预测的共嗯那个
还有两种分类的算法用到的不多，或者说是我用的不多，他们是半监督学习和强化学习，不过据说强化学习很厉害，有时间研究下！！！！
统计学习三要素
方法=模型+策略+算法
模型：就是要学习一个什么样的模型
策略：以怎样的方式来学习这个模型
算法：通过什么样的方法对模型进行求解
统计学习的三要素对所有分类的学习方法都适用，之后对所有方法的讨论都将遵循这三个要素！
这篇文章主要介绍下对监督学习介绍下！
监督学习
监督学习的模型
在监督学习过程中，模型的选择就是，下面两者之一
- 2018年1月17日补充(监督学习的整体逻辑)：从求解最终的决策函数的角度来看，在我们构建了模型之后，我们的目的一直都是要求出那些未知的参数，而所有的学习策略都是围着这个核心思想来展开的。求出参数有两者思路，一种是用解析式的方式直接求出来参数，就像线性回归的参数求解。另一种是在绝大多数的情况下我们无法解析式的方式来求解，而是走了一个曲线救国的思想就是”递归思想“（包括梯度上升/下降,批量梯度/随机梯度等）。而无论采用哪种思路去做，都要先有个关于参数的函数吧，之后才能研究是解析还是递归。该怎么得到这个函数呢？先归纳下我们有哪些已知条件，1.模型已知。2.有数据集。3.明确目的：求参数。好了，到这里很明显了，有数据集求参数，我们最常用的’极大似然估计’不就是专业做这个的么？但是我们想用这个估计方法就必须得知道模型中的哪一部分或整个模型符合什么概率分布，好，当我通过某些方法得到了概率分布，借助数据集和似然估计的思想就一定可以求出一个关于参数的函数，然后我们再考虑用解析还是递归继续求出参数，参数求出来后带回模型，我们的目的就达成了。明白了这个逻辑，我们就清楚的推断出为什么要做个损失函数/经验风险/结构函数这东西了么，往往这些函数是符合某种概率分布的，比如符合高斯分布，概率分布我都知道了，谁还能阻挡我求解使用极大似然估计来求接参数呢？？以上逻辑还需要随着时间的打磨不断优化，也许明天我就可能会推翻自己的结论。。。。谁知道呢？
回顾下”极大似然估计“
其核心思想就是，我现在知道了事情的结果了，我想知道是谁干的？
也就是说我知道了实验的结果，这个实验的分布模型我们已经知道了，但是这个模型里面一个参数是不知道的，那么我就去求让实验结果同时发生的概率（密度）最大化（最有可能发生）时候的参数是多少。
这个逻辑和我们正常已知分布模型和参数去求概率是个反向的过程
决策函数模型
此模型多少拥有回归算法
条件概率分布模型
此模型多少用于分类算法
2018年1月17日补充(广义分类)：其实这里提到的分类是狭义范围上的分类算法，也就是监督学习的分类。而我们也可以从广义范畴来认识”分类“，分类算法可分为监督学习，无监督学习（就是我们常说的聚类），半监督。
2018年1月17日补充(统计学习的目标)：我认为，既然统计学习方法的目的就是学习数据后预测数据,那么模型的设计思想必有相同之处,条件概率分布模型,其实不是我们最终想要得到的,我们想要的是把X喂给你,你告诉我是哪个分类就行,所以对这个模型就行包装下,当给定X时候,哪个条件概率分布越大就是哪个分类,而这其实也属于决策函数模型,所以我认为,至少在监督学习的这个范畴内,其目标都是求解一个”决策函数模型”!
监督学习的策略
监督学习中，一直在围绕着一个思想在做延伸，其实这种思想非常好理解。
比如我们自己做一个万能公式去预测一些数据，我们来怎么认定我们的万能公式是好的呢？所谓预测，就是预测值要无限的趋近于真实值，最理想的模型就是预测值=真实值，如果可以做到这点，那么我们这个模型就非常完美了，但现实中很难做到。所以我们就在我们的预测公式后面再加一项来弥补两者的误差—-**损失函数**L(Y,f(X))。
通常，损失函数的期望E[L(Y,f(X))]被定为为风险函数或期望损失。
那么问题来了，怎么求解风险函数呢？答案是，没办法求解，为什么呢？
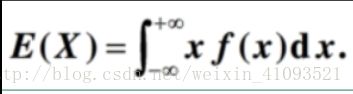
因为联合概率密度p(X,Y)是未知的，所以在无法通过这种方式求解，那我们就另辟蹊径！因为我们知道下面的公式：
根据这个原理，我们重构我们的风险函数，因为重构后的是根据经验数据得到的期望，故称其为经验风险：
好了，到此处，我们的学习策略从损失函数最小化升级为经验风险最小化。
应用这个经验风险有个前提条件就是（根据其原理公式），要在样本数据足够大的时候，根据大数定律，样本均值等于样本期望。
极大似然估计就是经验风险最小化的一个例子。当模型是条件概率分布且损失函数是对数函数时，经验风险最小化等价于极大似然估计。这一结论在线性回归推导中将得到应用。
但是，当样本容量很小，阶数过高时候，参数往往没有抑制项，就是说没人约束参数了，这样经验风险中的参数theta有时候就会很大，导致过拟合，所以为了解决这个问题，引出了“惩罚项”（正则项），也就是对经验函数进行正则化。从而抑制过拟合。
好了，到这里，我们将经验风险最小化升级为经验风险最小化或者结构风险最小化的问题。
监督学习的算法
其实这个很好理解,但此算法非彼算法,而是数学算法,就是在模型有了,策略有了的基础上,我们该通过什么样的数学思想来求出我们想要的东西的呢?这种思想就是这里说的监督学习的算法
我们所有的监督学习的学习策略都遵循这这一原则。
相信大家看完这篇能对整个统计学习方法,监督学习有个整体性的认识.我也刚刚接触算法不久肯定有很多不足!希望批评指正,接下来我将写监督学习的回归和分类算法的文章,希望能把所有的知识逻辑织成一个网.