莫队算法 --算法竞赛专题解析（26）

本系列文章将于2021年整理出版。前驱教材：《算法竞赛入门到进阶》 清华大学出版社
网购：京东 当当   作者签名书：点我
有建议请加QQ 群：567554289

有读者反映用某些浏览器看本文的公式有问题，特别是和根号有关的公式，不知为什么。
若有问题，请移步本文的博客园同步网址：https://www.cnblogs.com/luoyj/

阅读本文前，请先了解分块算法。参考我写的博客：
https://blog.csdn.net/weixin_43914593/article/details/108474903

1. 基础莫队算法

   莫队算法 = 离线 + 暴力 + 分块。
  （莫队：2010年信息学国家集训队队员莫涛。感谢莫涛对本文的图6提出修改意见。）
   “离线”和“在线”的概念。在线是交互式的，一问一答；如果前面的答案用于后面的提问，称为“强制在线”。离线是非交互的，一次性读取所有问题，然后一起回答，"记录所有步，回头再做”。
   基础的莫队算法是一种离线算法，它通常用于不修改只查询的一类区间问题，复杂度$O(n\sqrt{n})$，没有在线算法线段树或树状数组好，但是编码很简单。下面是一道莫队模板题。

---

HH项链 洛谷 1972
题目描述：给定一个数量，询问某个区间内不同的数有多少个。
输入：第一行一个正整数 n，表示数列长度。第二行n个正整数 ai。第三行一个整数m，表示HH 询问的个数。接下来 m 行，每行两个整数 L,R，表示询问的区间。
输出：输出m行，每行一个整数，依次表示询问对应的答案。

---

  题目询问区间内不同的数有多少个，即去重后数字的个数，本题的标准解法是线段树或树状数组。下面首先给出暴力法，然后再引导出莫队算法。

1.1 暴力法

   可以用STL的unique()函数去重，一次耗时O(n)，m次的总复杂度O(mn)。或者自己编码， 用扫描法统计数字出现的次数，这是一种简单易行的暴力法。
（1）查询一个区间有多少个不同的数字
   定义cnt[]，cnt[x]表示数字x出现的次数；定义答案为ans，即区间内不同的x有多少个。
   用指针L、R单向扫描，从数列的头扫到尾，L最终落在查询区间的最左端，R落在区间最右端。L往右每扫一个数x，就把它出现的次数cnt[x]减去1；R往右每扫到一个数x，就把它出现的次数cnt[x]加上1。扫描完区间后，cnt[x]的值就是x在区间内出现的次数。若cnt[x]=1说明x第1次出现，ans加1；若cnt[x]变为0，说明它从区间里消失了，ans减1。
   下面的例子是统计区间[3, 7]内有多少不同的数字，初始指针L=1，R=0。

图1 统计一个区间

  图(1)：L=1、R=0时，cnt[4]=0, cnt[7]=0, cnt[9]=0…答案ans=0。
  图(2)：L=2、R=0时，cnt[4]=-1, cnt[7]=0。
  图(3)：L=3、R=2时，cnt[4]=0, cnt[7]=0, cnt[9]=0…
  图(4)：L=3、R=3时，cnt[4]=0, cnt[7]=0, cnt[9]=1。出现了一个等于1的cnt[9]，答案ans = 1。
  图(5)：L=3、R=7时，cnt[4]=1, cnt[7]=0, cnt[9]=1, cnt[6]=2, cnt[3]=1,…其中cnt[4], cnt[9], cnt[6], cnt[3]都出现过等于1的情况，所以答案ans = 4。
（2）统计多个区间
   从上面查询一个区间的讨论可以知道，在L、R移动过程中，当它们停留在区间[L, R]时，就得到了这个区间的答案ans。那么对m个询问，只要不断移动L、R并与每个询问的区间匹配，就得到了m个区间询问的答案。
   为了方便操作，可以把所有询问的区间按左端点排序；如果左端点相同，再按右端点排序。讨论以下情况：
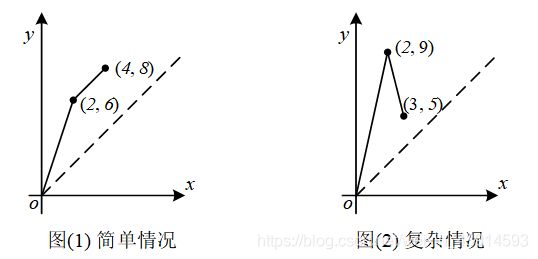
   1）简单情况，区间交错，区间[x1, y1]、[x2, y2]的关系是x1 ≤ x2，y1 ≤ y2。例如下图中，查询两个区间[2, 6]、[4, 8]。

图2 简单情况

  图(1)L、R停留在第1个区间上，得到了第1个区间的统计结果；图(2)L、R停留在第2个区间上，得到了第2个区间的结果。m次查询的m个区间，L、R指针只需要从左头到右（单向移动）扫描整个数组一次即可，总复杂度O(n)。
   2）复杂情况，既有区间交错，又有区间包含。区间[x1, y1]、[x2, y2]的包含关系是指x1 ≤ x2，y1 ≥ y2。例如下图中，区间[2, 9]包含了区间[3, 5]。此时L从头到尾单向扫描，而R指针却需要来回往复扫描，每次扫描的复杂度是O(n)。m次查询的总复杂度是O(mn)。

图3 复杂情况

  R往复移动的时候，R往左每扫一个数x，就把它出现的次数cnt[x]减去1。

1.2 区间查询问题的几何解释

  洛谷P1972的区间查询问题，可以概况为这样一种离线的几何模型：
  （1）m个询问对应m个区间，区间之间的转移，可以用L、R指针扫描，能以O(1)的复杂度从区间[L,R]移动到[L±1, R±1]。
  （2）把一个区间[L, R]看成平面上的一个坐标点(x, y)，L对应x，R对应y，那么区间的转移等同于平面上坐标点的转移，计算量等于坐标点之间的曼哈顿距离。注意，所有的坐标点(x, y)都满足x ≤ y，即所有的点都分布在上半平面上。
  （3）完成m个询问，等于从原点出发，用直线连接这m个点，形成一条“Hamilton路径”，路径的长度就是计算量。若能找到一条最短的路径，计算量就最少。
  Hamilton最短路径问题是NP难度的，没有多项式复杂度的解法。那么有没有一种较优的算法，能快速得到较好的结果呢？
  暴力法是按照坐标点(x, y)的x值排序而生成的一条路径，它不是好算法。例如下图(1)的简单情况，暴力法的顺序是好的；但是图(2)的复杂情况，暴力法的路径是(0, 0)-(2, 9)-(3, 5)，曼哈顿距离(2-0) + (9-0) + (3-2) + (9-5) = 16，不如另一条路径(0, 0)-(3, 5)-(2, 9)，曼哈顿距离 = 13。

图4 暴力法的路径

  下面介绍的莫队算法，提出了一种较好的排序方法。

1.3 莫队算法

  莫队算法把排序做了简单的修改，就把暴力法的复杂度从O(mn)提高到$O(n\sqrt{n})$。
  （1）暴力法的排序：把查询的区间按左端点排序，如果左端点相同，再按右端点排序。
  （2）莫队算法的排序：把数组分块（分成$\sqrt{n}$块），然后把查询的区间按左端点所在块的序号排序，如果左端点的块相同，再按右端点排序（注意不是按右端点所在的块排序，下一小节“莫队算法的几何解释”将说明原因）。
   除了排序不一样，莫队算法和暴力法的其他步骤完全一样。
   这个简单的修改是否真能提高效率？下面分析多种情况下莫队算法的复杂度。
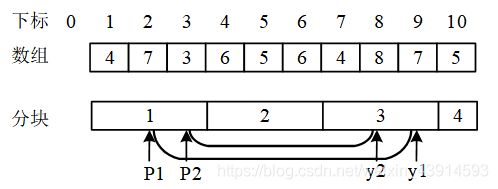
   （1）简单情况。区间交错，设区间[$P_1,y_1$]、[$P_2,y_2$]的关系是$P_1<P_2$，$y_1\le y_2$，其中$P_1、P_2$是左端点所在的块。L、R只需要从左到右扫描一次，m次查询的总复杂度是O(n)。
   （2）复杂情况。区间包含，设两个区间查询[$P_1,y_1$]、[$P_2,y_3$]的关系是$P_1=P_2，y_2\le y_1$。，如下图所示。

图5 按块排序后的区间包含

  此时小区间[$P_2,y_2$]排在大区间[$P_1,y_1$]的前面，与暴力法正好相反。在区间内，右指针R从左到右单向移动，不再往复移动。而左指针L发生了回退移动，但是被限制在一个长为 的块内，每次移动的复杂度是O($\sqrt{n}$)的。m次查询，每次查询左端点只需要移动O($\sqrt{n}$)次，右端点R共单向移动O(n)次，总复杂度O(n$\sqrt{n}$)。
   （3）特殊情况：m个询问，端点都在不同的块上，此时莫队算法和暴力法是一样的。但此时m小于 ，总复杂度O(mn) = O($\sqrt{n}$n)。

1.4 莫队算法的几何解释

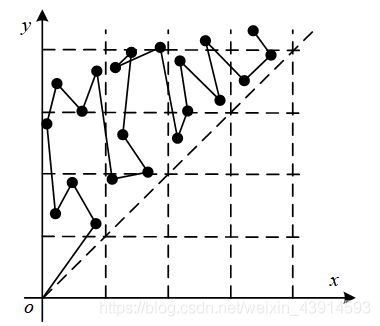
   莫队算法的几何意义见图6(感谢莫涛对此图提出修改意见)，这张图透彻说明了莫队算法的原理。图中的每个黑点是一个查询。
  图6(1)是暴力法排序后的路径，所有的点按x坐标排序，在复杂情况下，路径沿y方向来回往复，震荡幅度可能非常大（纵向震荡，幅度$O(n)$），导致路径很长。
  图6(2)是莫队算法排序后的路径，它把x轴分成多个区（分块），每个区内的点按y坐标排序，在区内沿x方向来回往复，此时震荡幅度被限制在区内（横向震荡，幅度$O(\sqrt{n})$），形成了一条比较短的路径，从而实现了较好的复杂度。

图6 暴力法和莫队算法的几何对比

  通过图6(2)可以更清晰地计算莫队算法的复杂度：
  （1）x方向的复杂度。在一个区块内，沿着x方向一次移动最多$\sqrt{n}$，所有区块共有m次移动，总复杂度$O(m\sqrt{n})$。
  （2）y方向的复杂度。在每个区块内，沿着y方向单向移动，整个区块的y方向长度是n，有$\sqrt{n}$个区块，总复杂度$O(n\sqrt{n})$。
  两者相加，总复杂度$O(m\sqrt{n}+n\sqrt{n})$，一般情况下题目会给出n = m。
  根据图6总结出莫队算法的核心思想：把暴力法的y方向的O(n) 幅度的震荡，改为x方向的受限于区间的O($\sqrt{n}$)幅度的震荡，从而减少了路径的长度，提高了效率。
  前面曾提到排序问题，对区间排序是先按左端点所在块排序，再按右端点排序，不是按右端点所在的块排序。原因解释如下：如果右端点也按块排序，几何图就需要画成一个方格图，方格中的点无法排序，实际的结果就是乱序。那么同一个方格内的点，在y方向上就不再是一直往上的复杂度为O(n)的单向移动，而是忽上忽下的往复移动，导致路径更长，复杂度变差。见图7所演示的路径。

图7 右端点按块排序是错误的

  编码时，还可以对排序做一个小优化：奇偶性排序，让奇数块和偶数块的排序相反。例如左端点L都在奇数块，则对R从大到小排序；若L在偶数块，则对R从小到大排序（反过来也可以：奇数块从小到大，偶数块从大到小）。
  这个小优化对照图6(2)很容易理解，图中路径在两个区块之间移动时，是从左边区块的最大y值点移动到右边区块的最小y值点，跨度很大。用奇偶性排序后，奇数块的点从最大y值到最小y值点排序，偶数块从最小y值点到最大y值点排序；那么奇数块最后遍历的点是最小y值点，然后右移到偶数块的最小y值点，这样移动的距离是最小的。从偶数块右移到奇数块的情况类似。
  下面是洛谷P1972的代码。莫队算法和暴力法唯一不同的地方在比较函数cmp()中。

#include
using namespace std;
const int maxn = 1e6;
struct node{         //离线记录查询操作
  int L, R, k;       //k：查询操作的原始顺序
}q[maxn];
int pos[maxn];
int ans[maxn];
int cnt[maxn];       //cnt[i]: 统计数字i出现了多少次
int a[maxn];
bool cmp(node a, node b){
	//按块排序，就是莫队算法：
	if(pos[a.L] != pos[b.L])        //按L所在的块排序，如果块相等，再按R排序
		return pos[a.L] < pos[b.L];
	if(pos[a.L] & 1)   return a.R > b.R; //奇偶性优化，如果删除这一句，性能差一点
	return a.R < b.R;     
		/*如果不按块排序，而是直接L、R排序，就是普通暴力法：
		if(a.L==b.L)  return a.R < b.R;
    	return a.L < b.L;   */
}
int ANS = 0;
void add(int x){     //扩大区间时（L左移或R右移），增加数x出现的次数
    cnt[a[x]]++;
    if(cnt[a[x]]==1)  ANS++;   //这个元素第1次出现
}
void del(int x){     //缩小区间时（L右移或R左移），减少数x出现的次数
    cnt[a[x]]--;
    if(cnt[a[x]]==0)  ANS--;   //这个元素消失了
}
int main(){	
    int n; scanf("%d",&n);
    int block = sqrt(n);         //每块的大小
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);       //读第i个元素
		pos[i]=(i-1)/block + 1;  //第i个元素所在的块
    }
    int m; scanf("%d",&m);          
    for(int i=1;i<=m;i++){       //读取所有m个查询，离线处理
        scanf("%d%d",&q[i].L, &q[i].R);
        q[i].k = i;              //记录查询的原始顺序
    }
    sort(q+1, q+1+m, cmp);       //对所有查询排序
	int L=1, R=0;                //左右指针的初始值。思考为什么？
    for(int i=1;i<=m;i++){
       	while(L<q[i].L)  del(L++);    //{del(L); L++;}  //缩小区间：L右移
        while(R>q[i].R)  del(R--);    //{del(R); R--;}  //缩小区间：R左移
		while(L>q[i].L)  add(--L);    //{L--; add(L);}  //扩大区间：L左移
        while(R<q[i].R)  add(++R);    //{R++; add(R);}  //扩大区间：R右移
        ans[q[i].k] = ANS;
    }
    for(int i=1;i<=m;i++)   printf("%d\n",ans[i]);  //按原顺序打印结果
    return 0;
}

2. 带修改的莫队

  上一节的基础莫队算法只用于无修改只查询的区间问题，如果是比较简单的“单点修改”，也能应用莫队算法，得到复杂度$O(m{n}^{\frac{2}{3}})$的算法。
  下面的例题是“单点修改 + 区间询问”。

---

数颜色 洛谷P1903
题目描述：有n个数（其中有些数可能相同），摆成一排。有以下操作：
Q L R 询问：从第L到第R个数，有几个不同的数。
R P Col 修改：把第P个数改成Col。
输入：第1行两个整数n，m，分别代表初始数量以及操作个数。
第2行n个整数，分别代表初始数列中第i个数。
第3行到第2 + m行，每行分别一个操作。
输出：对于每一个询问，输出一个数字，代表第L到第R个数共有几个不同的数。

---

  如果用莫队算法求解，必须离线，先把查询操作和修改操作分别记录下来。记录查询操作的时候，增加一个变量，记录本次查询前做了多少次修改。
  如果没有修改，就是基础莫队，一个查询的左右端点是[L, R]。加上修改之后，一个查询表示为(L, R, t)，t表示在查询[L, R]前进行了t次修改操作。可以把t理解为“时间”，t的范围是1 ≤ t ≤ m，m是操作次数。
  从一个查询移动到另一个查询，除了L、R发生变化外，还要考虑t的变化。如果两个查询的t相同，说明它们是基于同样的数列；如果t不同，两个查询所对应的数列是不同的，那么就需要补上这变化（直接用暴力法编程）。两个查询的t相差越小，它们对应的数列差别越小，计算量也越小，所以对t排序能减少计算量。
  与基础莫队一样，也可以给出带修改莫队的几何解释。基础莫队的左右端点[L, R]，对应平面上的点($x,y$) ，带修改的莫队(L, R, t)对应立体空间的($x,y,z$)。每个查询对应立体空间的一个点，那么从一个查询到另一个查询，就是从一个点($x_1,y_1,z_1$)到另一个点($x_2,y_2,z_2$)。计算复杂度仍然是两点之间的曼哈顿距离。
  模仿基础莫队的分块思路。定义带修改莫队的排序，按以下步骤执行：
   （1）按左端点L排序。若左端点L在同一个块，执行（2）。L对应$x$轴。
   （2）按右端点R排序。若右端点R在同一个块，执行（3）。R对应$y$轴。
   （3）按时间t排序。t对应$z$轴。
   左端点L所在的块是第1查询关键字，右端点R所在的块是第2关键字，时间t是第3关键字。
   x方向和y方向的分块，把$x$-$y$平面分成了方格，代表查询的点在方格内、方格间移动。
   根据带修改莫队的几何意义，计算算法的复杂度。这里先不采用 的分块方法，而是设一个分块的大小是B，共有n/B个分块。计算$x、y、z$三个方向上的复杂度：
  （1）$x$方向的复杂度（左端点指针L）。在一个区块内，沿着$x$方向一次最多移动B，所有的区块共有m次移动，总计算量 = $mB$。
  （2）$y$方向的复杂度（右端点指针R）。在一个区块内，沿着$y$方向一次最多移动B，所有的区块共有m次移动，总计算量 = $mB$。
  （3）$z$方向的复杂度（时间t）。每个被$x$和$y$区块限制的方格内，沿着$z$方向单向移动，最多移动m次，共$\frac{n^2}{B^2}$个方格，总计算量 =$\frac{m{n}^2}{B^2}$。
  三者相加，总计算量 = $mB+mB+\frac{m{n}^2}{B^2}$。当$B=n^{\frac{2}{3}}$时有较好的复杂度$O(m{n}^{\frac{2}{3}})$。
  作为对照，如果分块$B=\sqrt{n}$，复杂度是$O(mn)$，退化成了暴力法的复杂度。

3. 树上莫队

  基础莫队和带修改的莫队操作的都是一维数组。基于其他的数据结构的问题，如果能转换成一维数组而且是区间问题，那么也能应用莫队算法。
  典型的例子是树形结构上的路径问题，可以利用“欧拉序”把整棵树的结点顺序转化为一个一维数组，路径问题也变成了区间问题，就能利用莫队算法求解。下面的简单题体现了这个思路。

---

Count on a tree II 洛谷 SP10707
题目描述：给定有n个结点的数，每个结点有一种颜色。m次询问，每次询问给出两个结点u、v，回答从u到v的路径上有多少个不同颜色的结点。
输入：第一行是n和m，第二行有n个整数，第i个整数表示第i个结点的颜色。下面n-1行，每行有两个整数u、v，表示一个边(u, v)。下面m行，每行有两个整数u、v，表示一个询问，回答从结点u到v的路径上有多少个不同颜色的结点。
输出：对每个询问，输出一个整数。
数据范围：1 ≤ n ≤ 4×$10^4$，1 ≤ m ≤ $10^5$

---

思路：
1、把树的结点用欧拉序转为一维数组
  用DFS遍历树的结点，有两种遍历方式，得到两种欧拉序：
  （1）在每个结点第一次进和最后一次出都加进序列；
  （2）每遇到一个结点就把它加进序列。
  这里用第（1）种形式的欧拉序。下图的例子，欧拉序：{1, 2, 2, 3, 5, 5, 6, 6, 7, 7, 3, 4, 8, 8, 4, 1}。

图8 一棵树

  (u, v)上的路径有哪些结点？首先计算出u、v的lca(u, v)（最近公共祖先），然后讨论两种情况：
  （1）lca(u, v) = u或lca(u, v) = v，即u在v的子树中，或者v在u的子树中。例如u = 1, v = 6，区间是{1, 2, 2, 3, 5, 5, 6}，出现2次的结点{2, 5}不属于这条路径，因为它进来了又出去了。只出现一次的结点属于这条路径，即{1, 3, 6}。
  （2）lca(u, v) ≠ u且lca(u, v) ≠ v，即u和v都不在对方的子树上。此时u、v之间的路径需要通过它们的lca，但是lca没有出现在u和v的欧拉序区间内，需要添上。例如u = 5，v = 8，区间是{5, 6, 6, 7, 7, 3, 4, 8}，去掉出现2次的结点{6, 7}，剩下{5, 3, 4, 8}，再加上它们的lca = 1，得路径{5, 3, 4, 8, 1}。再例如u = 5，v = 7，区间是{5, 6, 6, 7}，去掉6，剩下{5, 7}，再加上它们的lca = 3，得路径{5, 7, 3}。
2、本题的求解步骤
  （1）求树的欧拉序，得到一维数组；求任意两个点的lca。编码时用树链剖分（做两次DFS）求欧拉序和lca。
  （2）把题目的查询(u, v)看成一维数组上的查询。题目要求查询(u, v)内不同的颜色，首先查区间(u, v)内只出现1次的结点，并加上u、v的lca，得到路径上的所有结点，然后在这些结点中统计只出现1次的数字。
  （3）用莫队算法，离线处理所有的查询，然后一起输出。注意分块时，本题的规模是2n，因为每个结点在欧拉序中出现2次；另外每个结点的颜色数值很大，需要离散化。