每日一题算法：2020年6月7日 单词接龙2 findLadders

2020年6月7日 单词接龙2 findLadders

默认格式：

class Solution {
    public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {

    }
}

解题思路：

其实看到这道题的时候稍微思考一会就能够发现，这道题其实就是考验我们使用拓扑数据结构的能力

拓扑结构算法需要的特点是什么？是一个有向无环图，那么我们的难点就转移为，如何将一个队列和两个字符变成一个有向无环图的数据结构。

生成拓扑图：

首先我们需要知道，我们要求的是一个最短的顺序，那么A->B，A->C，B->C同时成立的情况下，我们不希望存在B->C的这种情况，因为只会单纯地让步骤变长，所以我们希望在找到最短路径的之后直接将节点删除，这样后续的节点无法回头指向有更优道路的节点。

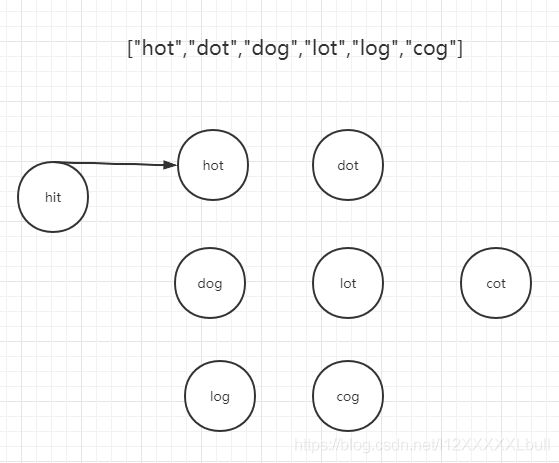
流程图示如下：

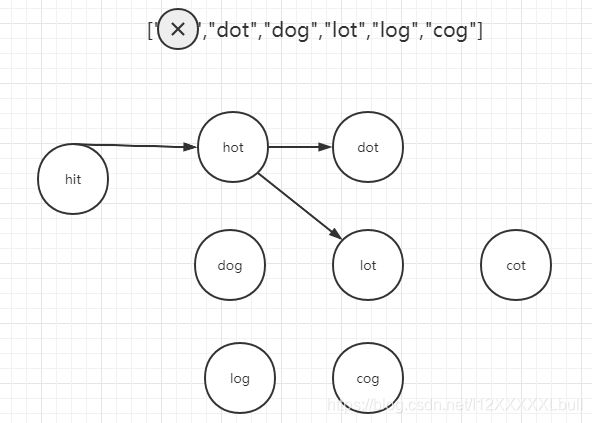
1，在链表中找到能够被hit连接的节点

2，把hot删除掉，然后测试hot所连接的所有节点。

3，删除掉dot和lot两个节点，然后对其后续节点进行连接（之前图画错了）

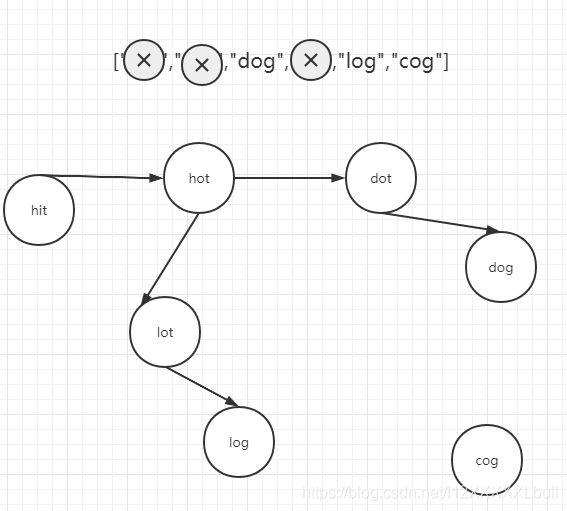
4，最后，当连接到关键的最终节点时，判断距离

因为第一次找到结束点时距离一定是最小的，所以距离只有和第一次一样才会记录。

字符串对比：

知道怎么创造拓扑图之后，还有一个问题，如何判断两个字符可以转换，这个其实很简单，遍历两个数组比较不一样的字符个数。

写个一部分代码。

    public boolean changeStr(String s1,String s2){
        int num=0;
        for (int i=0;i<s1.length()&&num>1;i++){
            if (s1.charAt(i)!=s2.charAt(i))
                num++;
        }
        if (num<=1)
            return true;
        else 
            return false;
    }

遍历拓扑图：

其实不需要建立实际的拓扑图也是没有关系的，因为在生成拓扑图的时候已经可以找到最短的转化序列了，所以实际上问题就在于如何将集合变成一个拓扑图，或者不是拓扑图，只是使用了拓扑图的思想。

难点在于如何构建这么一个结构，我想过通过删除已经得到过的节点来限制出现回路的想法。但是我发现删除是不能删除的，因为如果在处理之后直接删除必定会导致信息的丢失

比如有A->C,B->C,A->B,如果在计算A的子节点时，因为不需要计算A->C的最短路径不需要经过B，所以不希望计算A->B这一条路径，

放弃

直接看答案吧，今天又花了5个小时，还是没能做出来，现在实在是脑子很乱，没有办法想问题了。

之前一直都是理解错了，这并不属于拓扑，而是上一级的图，说道图就要说一说图的两种经典算法，广度优先算法和深度优先算法。

广度优先算法：

广度优先算法是需要遍历整个表的，将遍历过的节点记录下来，避免重复遍历，这样可以遍历整个图中的所有节点。广度优先算法就是为了遍历整个图的所有节点，而在这道题中，我们需要先通过广度优先算法来计算我们的最短路径。

深度优先算法：

深度优先算法是有选择地选择图的搜索顺序，在这题中的表现是在我们获得了图的最短路径后，我们可以通过深度优先算法得到我们需要的集合list。

在使用这些算法之前，首先要建立一个图。

BFS算法和DFS算法写一个方法来用，功能模块化

先分析BFS我们需要什么，我们需要将一个图中的各点到起点最短的距离，那么返回值就可以不需要，直接修改传入参数一个Map。

那还需要什么传入的参数吗？需要一个起点，需要一个图，需要一个终点，外加上面说的距离集合。

核心思路，用距离来表示有没有被访问过，代替标记数组。

public void BFS(Map<String,HashSet<String>> nodeMap,Map<String,Integer> Lenmap,String begin,String end){

    //首先要有一个链表来辅助
    List<String> list=new LinkedList<>();
    //设置一个起点
    list.add(begin);
    Lenmap.put(begin,0 );

    while(true){
        String now=list.get(0);

        //遍历节点的所有子数组
        for(String son:nodeMap.get(now)){
            //如果子数组的最短距离比该节点小，则证明不用替换更优的路线
            if (Lenmap.get(son)>Lenmap.get(now)+1){
                //否则就是当前距离+1
                Lenmap.put(son,Lenmap.get(now)+1);

                //而且表示是下一轮需要访问的节点，将其放入链表中
                list.add(son);

            }
        }
        //如果当前检点已经是end了，直接跳出结束方法
        if (now.equals(end))
            return;
        //把当前的访问完的给删除掉
        list.remove(0);
    }

}

然后是DFS深度优先算法，通过深度优先算法我们需要得到的是最终的结果链表集合，那么需要的参数是一个起点，一个终点，一个图，一个最短距离信息。同样写成一个方法。

为什么要写成一个方法的模式?因为需要用到递归的思想。同时，由于存在递归，每次递归的时候不能总是要构建一个链表的链表，所以，直接作为参数来传递。

DFS算法在这里的核心在于递归和回溯。

回溯算法的模板

之前都没有用过回溯算法，因为有些抽象所以没有能够很好的理解，现在来尝试着用用看回溯算法。

先把这模板上几个空的位置填上题目中的内容

到达目的，应该就是Str=endword

输出解，应该是给List集合中添加一个集合

方案数，应该是每个节点的时候的下一个节点数

方案可行，节点中存在下一个的距离正好是当前距离+1的值（这并不是方案可行，方案可行指的是必定为正确答案的情况，而本题中下一个节点的距离刚好是当前距离+1的值只是可能正确的道路）

在本题中对其修改，从尾部开始向头部查询，因为距离如果-1则必定是前面一个节点。

保存路径、再集合中加值

递归，对下一个值进行上述判断

回复之前的状态，把当前正在构造的List删除

public void DFS(Map<String,HashSet<String>> nodeMap,Map<String,Integer> Lenmap,String begin,String end){

    if(begin.equals(end)){

        nowlist.add(end);
        res.add(num,nowlist);
        num++;
        return;
    }

    //方案数，节点的所有子节点数
    for(String word:nodeMap.get(begin)){

        //如果下一个节点的长度是当前节点长度+1
        if (Lenmap.get(word)==Lenmap.get(begin)-1){
            nowlist.add(begin );
            DFS(nodeMap,Lenmap,word,end);
            nowlist=new LinkedList<>();
        }
    }

}

最后把差不多的功能给实现了

package month6;

import org.junit.Test;

import java.util.*;

public class findLadders {



    List<List<String>> res=new ArrayList<>();
    List<String> nowlist=new ArrayList<>();
    int num=0;



    public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {



        //用来存图的节点HashSet是下一个节点的地址
        Map<String,HashSet<String>> Nodemap=new HashMap<>();

        //用来存起点到每个节点的最短长度
        Map<String,Integer> Lenmap=new HashMap<>();

        wordList.add(beginWord);
        //初始化所有图节点，顺便初始化一下最短距离
        for(int i=0;i<wordList.size();i++){

            Nodemap.put(wordList.get(i),new HashSet<>());
            Lenmap.put(wordList.get(i), Integer.MAX_VALUE);
            //在找到能够成为下一个节点的节点
            for(int j=0;j<wordList.size();j++){

                //首先是能够匹配，而且不能是本身
                if (changeStr(wordList.get(i),wordList.get(j))&&i!=j){

                    //能连接的节点都加上
                    Nodemap.get(wordList.get(i)).add(wordList.get(j));
                }
            }
        }
        //找一下终点在不在，不存在直接返回空数组
        if(Nodemap.get(beginWord)==null)
            return new LinkedList<>();

        //把终点作为起点，起点作为终点开始计算路径
        Lenmap.put(endWord,0 );
        Lenmap.put(beginWord,Integer.MAX_VALUE );



//--------图做完了----------------

//        开始广度优先算法，算法直接写一个方法拿来用吧
        BFS(Nodemap,Lenmap ,endWord ,beginWord );

        DFS(Nodemap,Lenmap ,beginWord ,endWord);
        //计算完最短距离后，通过深度优先算法计算最短的路径的信息

        return res;
    }
        //判断字符串是否匹配的函数
        public boolean changeStr(String s1,String s2){
        int num=0;
        for (int i=0;i<s1.length();i++){
            if (s1.charAt(i)!=s2.charAt(i))
                num++;
        }
        if (num<=1)
            return true;
        else
            return false;
    }

        //广度优先算法，计算各点的距离起点的最短距离，通过Lenmap返回
        public void BFS(Map<String,HashSet<String>> nodeMap,Map<String,Integer> Lenmap,String begin,String end){

            //首先要有一个链表来辅助
            List<String> list=new LinkedList<>();
            //设置一个起点
            list.add(begin);
            Lenmap.put(begin,0 );

            while(true){
                String now=list.get(0);

                //遍历节点的所有子数组
                for(String son:nodeMap.get(now)){
                    //如果子数组的最短距离比该节点小，则证明不用替换更优的路线
                    if (Lenmap.get(son)>Lenmap.get(now)+1){
                        //否则就是当前距离+1
                        Lenmap.put(son,Lenmap.get(now)+1);

                        //而且表示是下一轮需要访问的节点，将其放入链表中
                        list.add(son);

                    }
                }
                //如果当前检点已经是end了，直接跳出结束方法
                if (now.equals(end))
                    return;
                //把当前的访问完的给删除掉
                list.remove(0);
            }

        }

        //深度优先算法
        public void DFS(Map<String,HashSet<String>> nodeMap,Map<String,Integer> Lenmap,String begin,String end){

            if(begin.equals(end)){

                nowlist.add(end);
                res.add(num,nowlist);
                num++;
                return;
            }

            //方案数，节点的所有子节点数
            List<String> oldlist=new LinkedList<>(nowlist);
            for(String word:nodeMap.get(begin)){

                //如果下一个节点的长度是当前节点长度+1
                if (Lenmap.get(word)==Lenmap.get(begin)-1){
                    nowlist.add(begin );
                    DFS(nodeMap,Lenmap,word,end);
                    nowlist=oldlist;
                }
            }

        }
}

今天实在是来不及了，这道题目难度太大了，我从早上8点半做到晚上十点也没能写完，不过让我学到了很多的知识也是不算太亏，最后也之差一点状态的转变就能够实现最终的目的了。

就是回溯的时候替换旧值实在是没有办法了，逻辑太复杂现在没有脑力去计算了。