数据结构与算法之五(递归与递归消除)

递归是一种函数调用自身的手法。比如阶乘，可以如此实现：

public long f(int n){
    if(n==1) return 1;   //停止调用
    return n*f(n-1);    //调用自身
}

》 上面也标出了递归两个特点。

》 递归的效率：方法调用是有一定开销的，同时每次调用方法时需要将方法参数和这个方法的返回地址压入栈中，如果调用次数太多，需要大量内存空间存储，可能引起栈溢出问题。所以递归并不是有效率的做法，但是它简化了问题。大事化小事。

》 分治算法：把一个大问题分成n个更小的问题来解决。递归的二分查找就是该算法的一个例子。还有归并排序，每次把序列分成两个子序列分别排序，最后合并。

》 汉诺塔问题，以前学c++的时候这个是比较好玩的。汉诺塔层数越高，移动越复杂，但是通过递归可以很快找出解决方案。不管多少层把它看作2部分，上面n层，下面1层。每次移动都是把上面n层移动到第二根柱子上，把最后一层移到第三根柱子上，再把上面n层移动到第三根柱子上。

》 归并排序，就是上面描述过的一种排序算法。在效率上比之前的简单排序是要高的，前面的简单排序效率是O(N^2),而归并排序只要O(N*log2(N))。实现大概如下：

public void mergeSort(int[] array, int low, int high){
    if(low==long){    //停止调用
        return;
    }
    int mid = (low+long)/2;
    mergeSort(array, low,mid);   //左边归并排序
    mergeSort(array,mid+1,high);   //右边归并排序
    merge(array, low,mid,high);   //合并左边和右边的有序数组
}

可以看出对于简化问题是有奇效的。归并排序的效率可以这样算：首先归并的层数，由于每次是2分我们知道是log2(N),每一层的merge方法要对所有N个元素进行复制，结果是N*log2(N)。它的缺点也很明显，由于需要拆分再合并，必须保留每次的数据，需要的内存空间比较多。

》消除递归。我们发现有一些算法用递归效率太低，比如阶乘，我们可以用一个for循环就搞定了。对于消除的递归的问题，一种常用的方法是用前面说的栈来做消除，模拟内存处理过程。
考虑我们前面讲的阶乘算法：

public long f(int n){
    if(n==1) return 1;   //停止调用
    return n*f(n-1);    //调用自身
}

递归通常有两个过程：
递归过程：不断递归入栈push，直到停止调用n=1
回溯过程：不断回溯出栈pop, 计算n*f(n-1)，直到栈空，结束计算。

可以把上述过程分为以下几个状态：

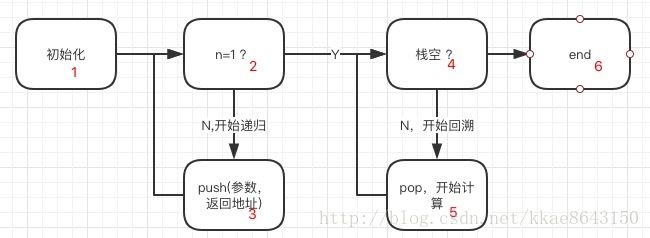
这样，我们利用这个状态机，用一个栈来存储数据，就可以完成整个计算。

//要存储的数据
class Data{
    //方法参数
    int n;
    //返回地址
    int returnAddress;
    //构造器及getter，setter
    ...
}

//栈
Stack myStack = new Stack<>();

//状态机实现运算过程
    public static int execute(int num){
        int i = 1;   
        int result = 1;
        while(i!=6){       //结束
            switch(i){
                case 1:     //初始化
                    i=2;
                    break;
                case 2:     //条件是否结束
                    if(num==1){
                        result=1;
                        i=4;
                    }else{
                        i=3;
                    }
                    break;
                case 3:     //递归入栈
                    Data data = new Data(num);
                    myStack.push(data);
                    num--;   //条件发生变化
                    i=2;
                    break;
                case 4:     //栈是否空
                    if(myStack.isEmpty()){
                        i=6;
                    }else{
                        i=5;
                    }
                    break;
                case 5:     //回溯出栈
                    Data data1 = myStack.pop();
                    result*=data1.n;
                    i=4;
                    break;
                }
        }
        return result;
    }

其实根据状态机来处理就很简单了。不过注意一点，本来栈存储的数据有参数，还有一个内存地址，这里为什么没有存内存地址就实现了？这个留给大家思考了。