后端-1

概述

状态估计的概率介绍

SLAM过程可由运动方程和观测方程来描述。那么，假设在t=0到t=N的时间内，有 x0 x 0 到 xN x N 那么多个位姿，并且有 y1,...,yM y 1 , . . . , y M 那么多个路标。运动和观测方程为：

{xk=f(xk−1,uk)+wkzk,j=h(yj,xk)+vk,jk=1,...,N,j=1,...,M { x k = f ( x k − 1 , u k ) + w k z k , j = h ( y j , x k ) + v k , j k = 1 , . . . , N , j = 1 , . . . , M

注意：

1. 观测方程中，只有当 xk x k 看到 yj y j 时，才会产生观测数据，否则就没有。事实上，在一个位置上通常只能观测到一小部分路标。而且，由于视觉SLAM特征点众多，所以实际当中观测方程数量远远大于运动方程数量。
2. 可能没有测量运动的装置，所以也有可能没有运动方程。在这种情况下，有若干种处理方式：认为确实没有运动方程，或假设相机不动，或者假设相机匀速运动。这几种方式都是可行的。在没有运动运动方程的情况下，整个优化问题就只由许多观测方程组成。这种就非常类似于SfM(structure from motion)问题，就相当于我们通过一组图像恢复运动和结构。与SfM不同的是，SLAM中的图像有时间上的先后顺序，而SfM允许使用完全无关的图像。
   由于位姿和路标点都是待估计的变量，改变一下记号，令 xk x k 为k时刻所有的未知量。它包含当前时刻的相机位姿和m个路标点。在这种记号的意义下，写成：
   
   xk≜{xk,y1,⋯,ym} x k ≜ { x k , y 1 , ⋯ , y m }

同时，把k时刻的所有观测基座 zk z k 。于是，运动方程与观测方程的形式更加简洁。

{xk=f(xk−1,uk)+wkzk=h(xk)+vk,j { x k = f ( x k − 1 , u k ) + w k z k = h ( x k ) + v k , j

现在考虑第k时刻的情况。我们希望通过0到k时刻中的数据，来估计现在的状态分布：

P(xk|x0,u1:k,z1:k) P ( x k | x 0 , u 1 : k , z 1 : k )

下表0:k表示0时刻到k时刻的所有数据。按照Bayes法则，把 zk z k 与 xk x k 交换位置，有：

P(xk|x0,u1:k,z1:k)∝P(zk|xk))P(xk|x0,u1:k,z1:k−1) P ( x k | x 0 , u 1 : k , z 1 : k ) ∝ P ( z k | x k ) ) P ( x k | x 0 , u 1 : k , z 1 : k − 1 )

第一项成为似然，第二项称为先验。似然由观测方程给出，而先验部分， xk x k 是基于所有过去状态估计得来的。至少它会受 xk−1 x k − 1 影响，于是按照 xk−1 x k − 1 时刻条件概率展开：

P(xk|x0,u1:k,z1:k−1)=∫P(xk|xk−1,u1:k,z1:k−1)P(xk−1|x0,u1:k,z1:k−1)dxk−1 P ( x k | x 0 , u 1 : k , z 1 : k − 1 ) = ∫ P ( x k | x k − 1 , u 1 : k , z 1 : k − 1 ) P ( x k − 1 | x 0 , u 1 : k , z 1 : k − 1 ) d x k − 1

如果我们考虑更久之前的状态，也可以继续对此式进行展开，但现在我们只关心k时刻和k-1时刻的情况。后续处理，存在若干种选择：其一是假设马尔可夫性，简单的一阶马氏性认为，k时刻状态只与k-1时刻状态有关，而与再之前的无关。如果做出这样的假设，我们就会得到以扩展卡尔曼滤波(EKF)为代表的滤波器方法。在滤波方法中，我们会从某时刻的状态估计，推导到下一时刻。另一种方法是依然考虑k时刻状态与之前所有状态的关系，此时将得到非线性优化为主题的优化框架。

线性系统和KF

当我们假设了马尔可夫性，从数学角度会发生哪些变化呢？

P(xk|xk−1,u1:k,z1:k−1)=P(xk|xk−1,uk) P ( x k | x k − 1 , u 1 : k , z 1 : k − 1 ) = P ( x k | x k − 1 , u k )

P(xk−1|x0,u1:k,z1:k−1)=P(xk−1|x0,u1:k−1,z1:k−1) P ( x k − 1 | x 0 , u 1 : k , z 1 : k − 1 ) = P ( x k − 1 | x 0 , u 1 : k − 1 , z 1 : k − 1 )

我们从形式最简单的线性高斯系统开始，最后会得到卡尔曼滤波器。线性高斯系统是说，运动方程和观测方程可以由线性方程来描述：

{xk=Akxk−1+uk+wkzk=Ckxk+vkk=1,⋯,N { x k = A k x k − 1 + u k + w k z k = C k x k + v k k = 1 , ⋯ , N

并假设所有的状态和噪声均满足高斯分布。记这里的噪声服从零均值高斯分布：

wk∼N(0,R).vk∼N(0,Q) w k ∼ N ( 0 , R ) . v k ∼ N ( 0 , Q )

现在，利用马尔可夫性，假设我们知道了k -1时刻的后验（在 k - 1 时刻看来）状态估计： x^k−1 x ^ k − 1 和它的协方差 P^k−1 P ^ k − 1 ，现在要根据 k 时刻的输入和观测数据，确定 xk x k 的后验分布。为区分推导中的先验和后验，我们在记号上作一点区别：以尖帽子 x^k x ^ k 表示后验，以横线 x¯¯¯k x ¯ k 表示先验分布。
卡尔曼滤波器的第一步，通过运动方程确定 xk x k 的先验分布。根据高斯分布的性质，显然有：

P(xk|x0,u1:k,z1:k−1)=N(Akx^k−1+uk,AkP^k−1ATk+R) P ( x k | x 0 , u 1 : k , z 1 : k − 1 ) = N ( A k x ^ k − 1 + u k , A k P ^ k − 1 A k T + R )

这一步成为预测，它显示了如何从上一时刻的状态，根据输入信息，推测当前时刻的状态的分布。这个分布也就是先验。记这里的：

x¯¯¯k=Akx^k−1+ukP¯¯¯¯k=AkP^k−1ATk+R x ¯ k = A k x ^ k − 1 + u k P ¯ k = A k P ^ k − 1 A k T + R

另一方面，由观测方程，我们可以计算在某个状态下，应该产生怎样的观测数据：

P(zk|xk)=N(Ckxk,Q) P ( z k | x k ) = N ( C k x k , Q )

为了得到后验概率，我们想要计算它们的乘积。虽然我们知道最后得到一个关于 xk x k 的高斯分布，但是计算上很麻烦，我们先把结果设为 xk∼N(x^k,P^k) x k ∼ N ( x ^ k , P ^ k ) ，那么：

N(x^k,P^k)=N(Ckxk,Q).N(x¯¯¯k,P¯¯¯¯k) N ( x ^ k , P ^ k ) = N ( C k x k , Q ) . N ( x ¯ k , P ¯ k )

这里我们稍微用点讨巧的方法。既然我们已经知道等式两侧都是高斯分布，那就只需比较指数部分即可，而无须理会高斯分布前面的因子部分。指数部分很像是一个二次型的配方，我们来推导一下。首先把指数部分展开，有：

(xk−x^k)TP^−1k(xk−x^k)=(zk−Ckxk)TQ−1(zk−Ckxk)+(xk−x¯¯¯k)TP−1k(xk−x¯¯¯k) ( x k − x ^ k ) T P ^ k − 1 ( x k − x ^ k ) = ( z k − C k x k ) T Q − 1 ( z k − C k x k ) + ( x k − x ¯ k ) T P k − 1 ( x k − x ¯ k )

为了求左侧的 x^k x ^ k 和 P^k P ^ k ，我们把两边展开，并比较 xk 的二次和一次系数。对于二次系数，有：

P^−1k=CTkQ−1Ck+P¯¯¯¯−1k P ^ k − 1 = C k T Q − 1 C k + P ¯ k − 1

该式给出了协方差的计算过程。为了便于后边列写式子，定义一个中间变量：

K=P^kCTkQ−1 K = P ^ k C k T Q − 1

则

P^kP^−1k=I=P^kCTkQ−1Ck+P^kP¯¯¯¯−1k=KCk+P^kP¯¯¯¯−1k P ^ k P ^ k − 1 = I = P ^ k C k T Q − 1 C k + P ^ k P ¯ k − 1 = K C k + P ^ k P ¯ k − 1

于是有：

P^k=(I−KCk)P¯¯¯¯k P ^ k = ( I − K C k ) P ¯ k

然后再比较一次项的系数，有：

−2x^TkP^−1kxk=−2zTkQ−1Ckxk−2x¯¯¯TkP¯¯¯¯−1kxk − 2 x ^ k T P ^ k − 1 x k = − 2 z k T Q − 1 C k x k − 2 x ¯ k T P ¯ k − 1 x k

整理得：

P^−1kx^k=CTkQ−1zk+P¯¯¯¯−1kx¯¯¯k P ^ k − 1 x ^ k = C k T Q − 1 z k + P ¯ k − 1 x ¯ k

两侧乘以 P^k P ^ k 得：

x^k=P^kCTkQ−1zk+P^kP¯¯¯¯−1kx¯¯¯k=Kzk+(I−KCk)x¯¯¯k=x¯¯¯k+K(zk−Ckx¯¯¯k) x ^ k = P ^ k C k T Q − 1 z k + P ^ k P ¯ k − 1 x ¯ k = K z k + ( I − K C k ) x ¯ k = x ¯ k + K ( z k − C k x ¯ k )

总结为预测和更新两步：

1. 预测：
   x¯¯¯k=Akx^k−1+ukP¯¯¯¯k=AkP^k−1ATk+R x ¯ k = A k x ^ k − 1 + u k P ¯ k = A k P ^ k − 1 A k T + R
2. 更新：先计算K，它又称为卡尔曼增益：
   K=P¯¯¯¯kCTk(CkP¯¯¯¯kCTk+Q)−1 K = P ¯ k C k T ( C k P ¯ k C k T + Q ) − 1
   然后就算后验概率的分布：
   x^k=x¯¯¯k+K(zk−Ckx¯¯¯k) x ^ k = x ¯ k + K ( z k − C k x ¯ k )
   P^k=(I−KCk)P¯¯¯¯k P ^ k = ( I − K C k ) P ¯ k

卡尔曼滤波器构成了线性系统的最优无偏估计。

非线性系统和EKF

SLAM中的运动方程和观测方程通常是非线性函数，尤其是视觉中的相机模型，需要使用相机内参模型以及李代数表示位姿，更不可能是一个线性系统。一个高斯分布，经过非线性变换后，往往不再是高斯分布，所以在非线性系统中，我们必须取得一定的近似，将一个非高斯的分布近似成一个高斯分布。把卡尔曼滤波器的结果拓展到非线性系统中来，称为扩展卡尔曼滤波器（Extended Kalman Filter，EKF）。通常的做法是，在某个点附近考虑运动方程和观测方程的一阶泰勒展开，只保留一阶项，即线性部分，然后按照线性系统进行推导。令k-1时刻的均值和协方差矩阵为 x^k−1,P^k−1 x ^ k − 1 , P ^ k − 1 。在k时刻，我们把运动方程和观测方程，在 x^k−1,P^k−1 x ^ k − 1 , P ^ k − 1 处进行线性化（相当于一阶泰勒展开），有：

xk≈f(x^k−1,uk)+∂f∂xk−1|x^k−1(xk−1−x^k−1)+wk x k ≈ f ( x ^ k − 1 , u k ) + ∂ f ∂ x k − 1 | x ^ k − 1 ( x k − 1 − x ^ k − 1 ) + w k

记这里的偏导数：

F=∂f∂xk−1|x^k−1 F = ∂ f ∂ x k − 1 | x ^ k − 1

同样的，对于观测方程：

zk≈h(x¯¯¯k)+∂h∂xk|x¯¯¯k+nk z k ≈ h ( x ¯ k ) + ∂ h ∂ x k | x ¯ k + n k

记这里的偏导数

H=∂h∂xk|x¯¯¯k H = ∂ h ∂ x k | x ¯ k

预测步骤中，根据运动方程有

P(xk|x0,u1:k,z0:k−1)=N(f(x^k−1,uk),FP^k−1FT+Rk) P ( x k | x 0 , u 1 : k , z 0 : k − 1 ) = N ( f ( x ^ k − 1 , u k ) , F P ^ k − 1 F T + R k )

这里的先验和协方差为

x¯¯¯k=f(x^k−1,uk),P¯¯¯¯k=FP^k−1FT+Rk x ¯ k = f ( x ^ k − 1 , u k ) , P ¯ k = F P ^ k − 1 F T + R k

考虑观测中，我们有

P(zk|xk)=N(h(x¯¯¯k)+H(xk−x¯¯¯k),Qk) P ( z k | x k ) = N ( h ( x ¯ k ) + H ( x k − x ¯ k ) , Q k )

根据Bayes展开式，可以推导 xk x k 的后验概率形式。
我们先定义一个卡尔曼增益 Kk K k ：

Kk=P¯¯¯¯kHT(HP¯¯¯¯kHT+Qk)−1 K k = P ¯ k H T ( H P ¯ k H T + Q k ) − 1

在卡尔曼增益的基础上，后验概率的形式为：

x^k=x¯¯¯k+Kk(zk−h(x¯¯¯k)),P^k=(I−KkH)P¯¯¯¯k x ^ k = x ¯ k + K k ( z k − h ( x ¯ k ) ) , P ^ k = ( I − K k H ) P ¯ k

在线性系统和高斯噪声情况下，卡尔曼滤波给出了无偏最优估计。而在SLAM这种非线性的情况下，他给出了单次线性近似下最大后验估计(MAP)。

EKF的讨论

非线性优化比滤波器占有明显的优势，但是在计算资源受限，带估计量比较简单的场合，EKF仍不失为一种有效的方式。
EKF有哪些局限性？

1. 首先，滤波器方法在一定程度上假设了马尔可夫性，也就是k时刻的状态只与k-1时刻相关，而与k-1之前的状态与观测无关（或者和前几个有限时间的状态相关）。这里有点类似于视觉里程计，只考虑相邻两帧关系一样。如果当前帧真的与很久之前的数据相关，那么滤波器很难处理这种情况。而非线性优化则倾向于使用所有的历史数据。它不光考虑临近时刻的特征点与轨迹关系，更会吧考虑很久之前的状态考虑进来，称为全体时间上的SLAM（FULL SLAM）。在这种意义下，非线性优化算法使用更多的信息，当然也需要更多的计算。
2. EKF滤波器仅在 x^k−1 x ^ k − 1 出做了一次线性化，存在非线性误差。
3. 从程序实现上来说，EKF需要存储状态量的均值和方差，并对他们进行维护和更新。如果把路标也放进状态的话，由于视觉SLAM中路标数量很大，这个数量是相当大的，且与状态呈平方增长。因此EKF SLAM被普遍认为不可适用于大型场景。

BA与图优化

Bundle Adjustment，是指从视觉重建中提取最优的3D模型和相机参数（内参数和外参数）。从每一个特征点反射出来的技术光线，在我们把相机姿态和特征点空间位置做出最优的调整后，最后收束到相机光心的过程，我们简称BA。
在以图优化框架的视觉SLAM算法中，BA起到了核心作用。它类似于求解只有观测方程的SLAM问题。

投影模型和BA代价函数

从一个世界坐标系中的点 p p 出发，把相机的内外参数和畸变都考虑进来，最后投影成像素坐标，一共需要以下几步：

1. 首先，把世界坐标转换到相机坐标，这里将用到相机外参数 (R,t) ( R , t ) ：
   P′=Rp+t=[X′,Y′,Z′]T. P ′ = R p + t = [ X ′ , Y ′ , Z ′ ] T .
2. 然后将 P′ P ′ 投至归一化平面，得到归一化坐标：
   Pc=[uc,vc,1]T=[X′/Z′,Y′/Z′,1]T P c = [ u c , v c , 1 ] T = [ X ′ / Z ′ , Y ′ / Z ′ , 1 ] T
3. 对归一化坐标去畸变，得到几畸变后坐标。这里暂时只考虑镜像畸变：
   {u′c=uc(1+k1r2c+k2r4c)v′c=vc(1+k1r2c+k2r4c) { u c ′ = u c ( 1 + k 1 r c 2 + k 2 r c 4 ) v c ′ = v c ( 1 + k 1 r c 2 + k 2 r c 4 )
4. 最后，根据内参模型，计算相机坐标：
   {us=fxu′c+cxvs=fyv′c+cy { u s = f x u c ′ + c x v s = f y v c ′ + c y
   
   这一系列过程的流程图，如下：
   
   这个过程也就是前面讲的观测方程，之前把他抽象的记成：
   
   z=h(x,y) z = h ( x , y )
   
   现在给出他的详细参数化过程。具体的说，这里的x指代此时相机的位姿，即外参 R,t R , t ,它对应的李代数为 ξ ξ .路标 y y 即这里的三维点 p p ,而观测数据则是像素坐标 z≜[us,vs]T z ≜ [ u s , v s ] T 。以最小二乘的角度来考虑，可以列写此次观测的误差：
   e=z−h(ξ,p) e = z − h ( ξ , p )
   
   然后，把其他时刻的观测量也考虑进来，给误差添加一个下标。设 zij z i j 为位姿 ξi ξ i 处观察路标 pj p j 产生的数据，那么整体的代价函数（Cost Function）为：
   
   12∑i=1m∑j=1n||zij−h(ξi,pj)||2. 1 2 ∑ i = 1 m ∑ j = 1 n | | z i j − h ( ξ i , p j ) | | 2 .
   
   对这个最小二乘进行求解，相当于对位姿和路标同时作了调整，也就是所谓的BA。

BA的求解

观察观测模型 h(ξ,p) h ( ξ , p ) ,其不是线性函数，所以我们通过一些非线性手段来优化他。根据非线性优化的思想，我们应该从某个初始值开始，不断的寻找下降方向 △x △ x 来找到目标函数的最优解，即不断地求解增量方程中的增量 △x △ x 。尽管误差项都是针对单个位姿和路标点的，但在整体BA目标函数上必须把自变量定义成所有待优化的变量：

x=[ξ1,⋯,ξm,p1,⋯,pn]T. x = [ ξ 1 , ⋯ , ξ m , p 1 , ⋯ , p n ] T .

相应的，增量方程中的 △x △ x 则是对整体自变量的增量。在这个意义下，当我们给出自变量的一个增量时，目标函数变为：

12||f(x+△x)||2≈12∑i=1m∑j=1n||eij+Fij△ξi+Eij△pj||2 1 2 | | f ( x + △ x ) | | 2 ≈ 1 2 ∑ i = 1 m ∑ j = 1 n | | e i j + F i j △ ξ i + E i j △ p j | | 2

其中， Fij F i j 表示整个代价函数在当前状态下对相机姿态的偏导数，而 Eij E i j 标识该函数对路标点位置的偏导。
把相机位姿点放在一起：

xc=[ξ1,ξ2,⋯,ξm]T∈R6m, x c = [ ξ 1 , ξ 2 , ⋯ , ξ m ] T ∈ R 6 m ,

把空间点的变量也放在一起：

xp=[p1,p2,⋯,pn]T∈R3n x p = [ p 1 , p 2 , ⋯ , p n ] T ∈ R 3 n

那么可以得到如下

12||f(x+△x)||2=12||e+F△xc+E△xp||2 1 2 | | f ( x + △ x ) | | 2 = 1 2 | | e + F △ x c + E △ x p | | 2

需要注意的是，该式从一个由很多小型二次型之和，变成了一个更整体的样子。这里的雅克比矩阵 E E 和 F F 必须是整体目标函数对整体变量的导数，它将是一个很大块的矩阵，而里头的每个小分块，需要由每个误差项的导数 Fij F i j 和 Eij E i j “拼凑起来”，然后无论我们使用 G−N G − N 还是 L−M L − M 方法，最后都将面对增量线性方程：

H△x=g H △ x = g

我们知道 G−N G − N 和 L−M L − M 的主要区别在于，这里的 H H 是取 JTJ J T J 还是 JTJ+λI J T J + λ I 的形式。由于我们把变量归类成位姿和空间点两种，所以雅克比矩阵可以分块为：

J=[FE] J = [ F E ]

那么以 G−N G − N 为例，则 H H 矩阵为：

H=JTJ=[FTFETFFTEETE] H = J T J = [ F T F F T E E T F E T E ]

当然 L−M L − M 中我们也需要计算这个矩阵，不难发现，因为考虑了所有的优化变量，这个线性方程的维数将非常大，包含了所有的相机位姿和路标点。尤其是在视觉SLAM中，一个图像就会提取数百个特征点，大大增加了这个线性方程的规模。如果直接对 H H 求逆来计算增量方程，由于矩阵求逆是复杂度为 O(n3) O ( n 3 ) 的操作，这是非常消耗计算资源的。幸运的是，这里的 H H 矩阵是有一定特殊结构的。利用这个特殊结构我们可以加速求解过程。

稀疏性和边缘化

H H 矩阵的稀疏性是由雅克比 J(x) J ( x ) 引起的。考虑这些代价函数中的其中一个 eij e i j 。注意到这个误差项只描述了在 ξi ξ i 看到 pj p j 这件事，只涉及到第 i i 个相机位姿和第 j j 个路标点，对其余变量的导入都为0。所以该误差对应的雅克比矩阵有下面的形式：

Jij(x)=(02×6,⋯02×6,∂eij∂ξi,02×6,⋯02×3,⋯02×3,∂eij∂pj,02×3,⋯02×3) J i j ( x ) = ( 0 2 × 6 , ⋯ 0 2 × 6 , ∂ e i j ∂ ξ i , 0 2 × 6 , ⋯ 0 2 × 3 , ⋯ 0 2 × 3 , ∂ e i j ∂ p j , 0 2 × 3 , ⋯ 0 2 × 3 )

其中 02×6 0 2 × 6 表示为纬度为 2×6 2 × 6 的 0 0 矩阵，同理 02×3 0 2 × 3 也一样。该误差对相机姿态的偏导 ∂eij/∂ξi ∂ e i j / ∂ ξ i 的维度为 2×6 2 × 6 对路标点的偏导 ∂eij/∂pj ∂ e i j / ∂ p j 的维度为 2×3 2 × 3 。这个误差项的雅克比矩阵，除了这两处为非零块之外，其余地方都为零。这体现了该误差项与其他路标与轨迹无关的特性。那么，他对增量方程有什么影响呢？ H H 矩阵为什么会产生稀疏性呢？

当某个误差项 J J 具有稀疏性时，它对 H H 的贡献也具有稀疏形式

设 Jij J i j 只在 i,j i , j 处有非零块，那么它对 H H 的贡献为 JTijJij J i j T J i j ，具有示意图上所显示的稀疏形式。这个 JTijJij J i j T J i j 仅有四个非零块，位于 (i,i),(i,j),(j,i),(j,j) ( i , i ) , ( i , j ) , ( j , i ) , ( j , j ) 。对于整体 H H ，由于：

H=∑i,jJTijJij H = ∑ i , j J i j T J i j

请注意 i i 在所有的相机的位姿中取值， j j 在左右路标点中取值。我们把 H H 进行分块：

H=[H11H21H12H22] H = [ H 11 H 12 H 21 H 22 ]

这里的 H11 H 11 只和位姿点有关， H22 H 22 只和路标点有关。当我们遍历 i,j i , j 时，下列事实总是成立的：

1. 不管 i,j i , j 怎么变， H11 H 11 都是对角阵，只有 Hii H i i 处有非零块。
2. 同理， H22 H 22 都是对角阵， Hjj H j j 处有非零块。
3. 对于 H12 H 12 和 H21 H 21 ,有可能稀疏有可能稠密，视具体的情况而定。

这显示了矩阵的稀疏结构，之后对线性方程的求解，也是利用它的稀疏结构。
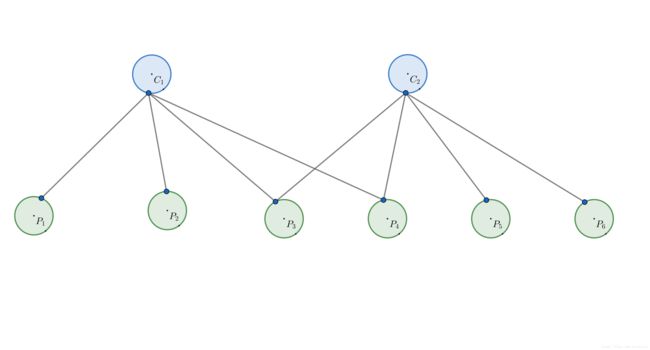
我们这里简单举例说明。假设一个场景里面有2个相机位姿 (C1,C2) ( C 1 , C 2 ) 和6个路标 (P1,P2,P3,P4,P5,P6) ( P 1 , P 2 , P 3 , P 4 , P 5 , P 6 ) 。相机位姿和路标点所对应的变量分别为 ξi,i=1,2 ξ i , i = 1 , 2 , Pj,j=1,⋯,6 P j , j = 1 , ⋯ , 6 。 C1 C 1 观测到路标点 P1,P2,P3,P4 P 1 , P 2 , P 3 , P 4 , C2 C 2 观测到路标点 P3,P4,P5,P6 P 3 , P 4 , P 5 , P 6 。

可以推测BA的目标函数为：

12(||e11||2+||e12||2+||e13||2+||e14||2+||e23||2+||e24||2+||e25||2+||e26||2) 1 2 ( | | e 11 | | 2 + | | e 12 | | 2 + | | e 13 | | 2 + | | e 14 | | 2 + | | e 23 | | 2 + | | e 24 | | 2 + | | e 25 | | 2 + | | e 26 | | 2 )

这里的 eij e i j 使用之前定义过的代价函数。以 e11 e 11 为例，它描述在 C1 C 1 看到 P1 P 1 这件事，与其它的相机位姿和路标无关。记 J11 J 11 为 e11 e 11 对应的雅克比矩阵，不难看出 e11 e 11 对 ξ2 ξ 2 和 P2,⋯,P6 P 2 , ⋯ , P 6 的偏导数都为0。我们把所有变量以 (ξ1,ξ2,p1,⋯,p6)T ( ξ 1 , ξ 2 , p 1 , ⋯ , p 6 ) T 的顺序摆放，则有：

J11=∂e11∂x=(∂e11∂x11,02×6,∂e11∂p1,