最小生成树 Prime算法
问题背景:
对于一个图,它的所有生成树中必有一个“边的权值最小”的生成树,我们把它称为最小生成树。
概念很抽象,换做实际问题:
有十个城市,各个城市之间距离或远或近。需要建设一个道路网,把十个城市连接在一起,要求道路网的道路长度最小。
各个城市的连接可以抽象为一个图,本质上即是求该图的一个最小生成树。
每一个图可能有多个生成树,但最小生成树 所有边的权值之和是最小的。
Prime算法简介:
最小生成树和最短路径一样,都是在实际中非常常见的图算法问题。
同样也有专门的算法来构造图的最小生成树。
Prime算法是求解最小生成树问题最常用的算法,思想和上次讲解的 最短路径Dijkstra算法 有些接近。
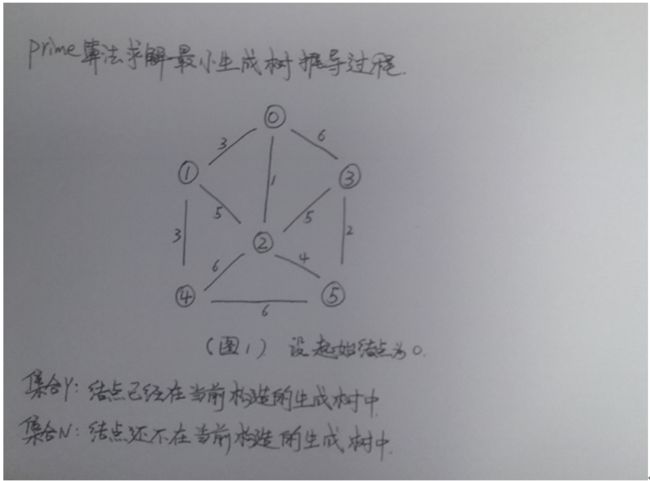
1. 把所有节点分成两类,一类是已经加入到了 当前的生成树中(集合 Y) ,一类是还没有加入当前的生成树中(集合N)。
PS: 1. 显然,这种分类可以用flag来设置。
2. 最终的生成树是一步一步构造的,所以说是 “当前的”生成树。
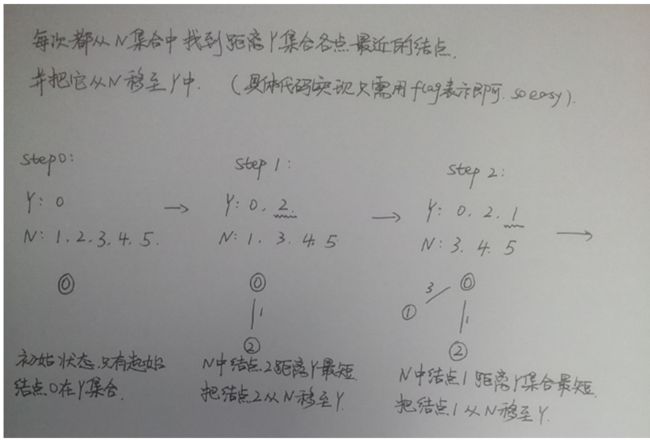
2. 从 Y 中取得一个节点 Vy, 从 N 中取得一个节点 Vn. 使其满足 Vy和Vn之间边的权值最小。
3、 找到满足上述条件的节点后,把Vn结点从 N 移入 Y中。
Ps: 具体代码实现是,flag值修改即可。 (最原始的做法,后续会有改进方式)
3. 重复上述 2. 3. 两步,直到所有节点全部加入Y中。
具体例子:
代码转化与具体实现:
代码实现时需要注意的几个问题:
1. 如何表示集合Y 和集合 N
当然,可以使用一个flag数组表示,比如为true表示在Y中,false在N中。
2. 集合Y和集合N中均可能有多个节点,如何从N集合中找到符合条件(距离Y中所有节点最近)的结点?
最粗暴的方法,每次都分别遍历 Y 和 N集合,两重遍历可以找到N中的该结点,但是效率会很差。可以从数据结构设计的角度改善。
建立一个数组, int minDis[ N ]
对于其中元素 minDis[i],其含义是 j 节点到 Y 集合所有节点距离的最小值。
寻找N中符合条件的结点时,只需要遍历N集合中结点minDis的数据,找到最小值即可。
显然,对于Y集合中的结点 i ,minDis[i]都是 0.
这样,minDis数组也可以替代上步中的flag数组: minDis值是0,即代表结点在Y集合中。
3. 每次从N集合中找到符合条件的结点 i 后,都需要做哪些处理?
首先,要把它从N移动到Y中。 minDis[i] = 0 即可。(原因参考上步的说明)
其次,要判断是否需要更新N中剩余结点 mindDis的值。
因为minDis[j] 存储的是j结点到Y中所有结点距离的最小值,当把i结点从N移动到Y中后,Y集合元素增多,对于N中剩余结点j而言,minDis[j]的值可能会减小。
什么情况下该值会减小?
当从N移动到Y中的结点 I 距离 j结点的值 小于 当前 minDis[j]的值,就需要更新minDis.
参考代码:
#define N 100
int matrix[N][N];
//最小生成树信息
int treeLenthResult = 0; //最终生成的最小生成树 边的权值之和
int minDis[N];
int closeVertex[N];
//设置起始结点下标是0 (从顶点0开始构造)
//初始化minDis
for (int i = 0; i < N; i++) {
minDis[i] = matrix[i][0];
closeVertel[i] = 0;
}
//起始结点初始化
minDis[0] = 0;
closeVertel[0] = 0;
//N-1次遍历,每次都从集合N中找到一个结点,距离集合Y中所有结点值最小
for (int i = 1; i < N; i++) {
int tmpDis = INF;
int tmpLoc = -1;
for (int j = 0; j < N; j++) {
//minDis[j] != 0 --> j结点不在当前的生成树中
if ((minDis[j] != 0) && (minDis[j] < tmpDis) ) {
tmpDis = minDis[j];
tmpLoc = j;
}
}
if (tmpLoc != -1) {
//tmpLoc结点 是本轮循环中找到的目标结点
//更新当前得到生成树边的权值之和
treeLenthResult += tmpDis;
}
//tmpLoc结点从N结合移至Y集合
minDis[tmpLoc] = 0;
//更新N集合中剩余的其他结点
for (int j = 0; j < N; j++) {
if (minDis[j] > matrix[j][tmpLoc]) {
minDis[j] = matrix[j][tmpLoc];
closeVertex[j] = tmpLoc; //此时,j结点距离Y集合中 tmpLoc结点最近
}
}
}