数据结构笔记（七）——二项队列（binomial queue）（3）

左式堆将插入、合并和删除最小元的操作控制在O(logN)，尽管时间已经够少了，但二项队列进一步降低了这个时间。二项队列（binomial tree）以最坏时间O（logN）支持以上操作，并且插入操作平均花费常数时间。

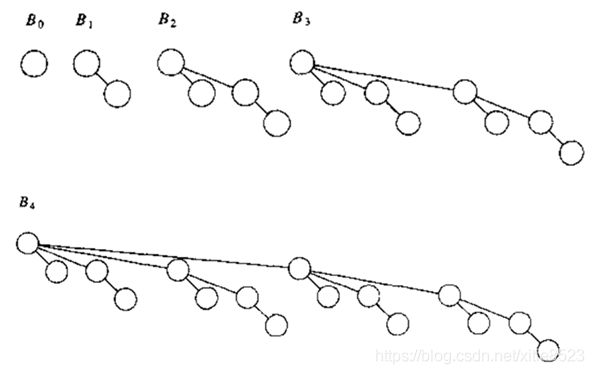
二项队列不是一棵树，而是树的集合，称为森林，这里的树有特定的形式，同时也具有堆序性，叫做二项树（binomial tree）。如图为一个二项队列，有B0,B1,B2,B3,B4五棵二项树。可以看到，二项队列具有以下特性：

1、高度为k的二项树Bk通过将高度为Bk-1的二项树接到另外一棵高度为Bk-1的二项树的根上构成。

2、二项树Bk由一个带有儿子B0，B1·····Bk-1的根组成（形状上），从Bk的构成过程可以知道这个特性，在构成B3的过程中，经历了根节点接上B0，B1，B2的过程。

3、高度为k的树有2^k个节点，第k棵树的节点会等于第k-1棵树的节点*2，那么B0，B1，B2的节点数就是这样子往后推。

4、对于每个Bk，深度d处的节点数为二项系数.

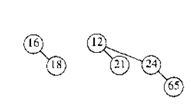
在这种结构中如何存储数据呢？如图，6个元素存储在二项树中，6=0110，对应B1，B2。第i棵二项树有2^i个节点，这与二进制不谋而合，第i棵二项树的对应二进制的第i位。二项队列中的每棵树都要满足堆序性，如下图。

二项队列的操作主要有插入，合并，删除最小元，插入的操作可以看成只有单个节点的二项队列和另一个二项队列的合并。合并操作中很重要的部分是合并两棵高度相等的树。二项树具有多个孩子节点，我们用一般树的表示方法：每个节点的儿子都存在一个链表中，每个节点都有一个指向他的第一个儿子和第一个兄弟的指针。为了操作简单，二项树的子树采用递减的顺序（二项队列存储二项树仍是按照高度递增排序的）。因为新的子树将会是最大的子树，将它作为第一个儿子比将它作为最后一个儿子（要遍历孩子链表将新的子树放在链表末尾）更加方便。

struct Node
{
	ElementType element;
	Position left_child;
	Position next_sibling;
};

合并两棵高度相同的二项树：

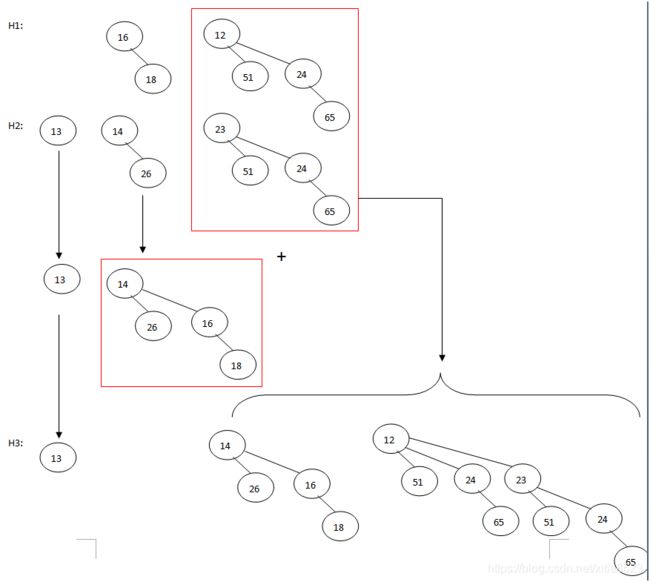
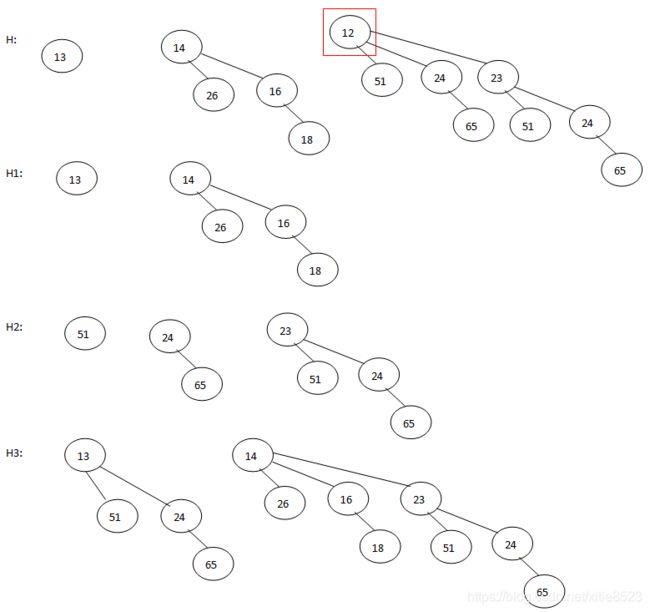
如下图，将H1和H2合并为H3，只有H2有高度为0的二项树，将其放入H3中；合并高度为1的二项树得到高度为2的二项树，现在有3个高度为2的二项树，将其中一个放入H3中，另外两个合并得到高度为3的二项树放入H3中。每次合并同样大小的二项树花费常数时间，总共有O（logN）棵二项树，因此合并的最坏情形下花费时间为O（logN）（所有高度H1，H2都有二项树，任意高度的二项树都要合并）。

 

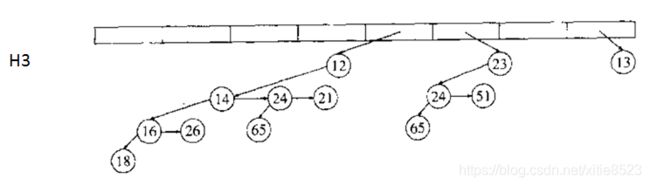
删除最小元可以在所有的二项树的根节点寻找最小值，找到最小值所在的树，删除它的根节点，那么这棵树将会分解成若干个子树，我们把这些子树重新构成一个二项队列与原来的二项队列（去掉了一棵二项树）合并。找出最小元及构造新的队列花费时间O（logN），合并队列花费O（logN），整个deleteMin的代价是O(logN)。删除H的最小元如下图：

代码中有一些需要注意的点：

BinQueue.h

#pragma once
#include
using namespace std;
typedef int ElementType;
#define MAXTREES (14)//最大节点数为2^14-1
#define CAPACITY (16383)//2^14-1
#define INFINITY (32768)
struct Node;
struct Collection;
typedef Node *Position;
typedef Position BinTree;
typedef Collection *BinQueue;
BinQueue initialize();
BinQueue makeEmpty(BinQueue q);
BinQueue insertX(BinQueue q, ElementType e);
ElementType deleteMin(BinQueue q);
ElementType findMin(BinQueue q);
BinQueue merge(BinQueue q1, BinQueue q2);
int isEmpty(BinQueue q);
int IsFull(BinQueue q);
void destroy(BinQueue q);
struct Node
{
	ElementType element;
	Position left_child;
	Position next_sibling;
};
struct Collection//二项队列
{
	int current_size;//当前节点数
	BinTree trees[MAXTREES];//森林中的二项树
};

BinQueue.cpp

#include "stdafx.h"
#include "BinQueue.h"
BinQueue initialize()
{
	BinQueue bq = (BinQueue)malloc(sizeof(Collection));
	if (bq==nullptr)
	{
		cerr << "out of space" << endl;
		return nullptr;
	}
	bq->current_size = 0;
	for (int i=0;itrees[i] = nullptr;
	}
	return bq;
}
void destroyTree(BinTree bt)
{
	if (bt==nullptr)
	{
		return;
	}
	destroyTree(bt->left_child);
	destroyTree(bt->next_sibling);
	free(bt);
}
void destroy(BinQueue q)
{
	if (q==nullptr)
	{
		return;
	}
	for (int i = 0; i < MAXTREES; ++i)
	{
		destroyTree(q->trees[i]);
	}
	free(q);
}
BinQueue makeEmpty(BinQueue q)
{
	if (q != nullptr)
	{
		for (int i = 0; i < MAXTREES; ++i)
		{
			destroyTree(q->trees[i]);
		}
		for (int i=0;itrees[i] = nullptr;
		}
		q->current_size = 0;
	}
	return q;
	
}
BinQueue insertX(BinQueue q, ElementType e)
{
	BinTree new_tree = (BinTree)malloc(sizeof(Node));
	if (new_tree==nullptr)
	{
		cerr << "out of space" << endl;
		return q;
	}
	new_tree->element = e;
	new_tree->left_child = new_tree->next_sibling = nullptr;
	BinQueue new_queue = initialize();
	new_queue->current_size = 1;
	new_queue->trees[0] = new_tree;
	return merge(q, new_queue);

}
ElementType deleteMin(BinQueue q)
{
	if (isEmpty(q))
	{
		cerr << "binomial queue is empty" << endl;
		return -INFINITY;
	}
	int min_tree_i;
	ElementType min_data = INFINITY;
	BinTree delete_tree;
	Position delete_node;
	BinQueue delete_queue;
	for (int i=0;itrees[i]!=nullptr)&&(q->trees[i]->elementtrees[i]->element;
		}
	}
	delete_tree = q->trees[min_tree_i];
	delete_node = delete_tree;
	delete_tree = delete_tree->left_child;
	free(delete_node);
	delete_queue = initialize();
	for (int j=min_tree_i-1;j>=0;--j)//最小值所在子树的高度为min_tree_i，除去根节点的其他子树的高度为min_tree_i-1~0
	{
		delete_queue->trees[j] = delete_tree;//用最小值所在子树剩余的节点创建一个新的队列
		delete_tree = delete_tree->next_sibling;
		delete_queue->trees[j]->next_sibling = nullptr;
	}
	delete_queue->current_size = (1 << min_tree_i) - 1;//1向左移动min_tree_i位，如移动3位，00000001—>00001000
	q->trees[min_tree_i] = nullptr;
	q->current_size -= delete_queue->current_size + 1;//+的优先级比-=的优先级高
	q = merge(q, delete_queue);
	return min_data;
}
ElementType findMin(BinQueue q)
{
	if (isEmpty(q))
	{
		cerr << "binomial queue is empty" << endl;
		return -INFINITY;
	}
	ElementType min_data = INFINITY;
	for (int i = 0; i < MAXTREES; ++i)
	{
		if ((q->trees[i]!=nullptr) && (q->trees[i]->element < min_data))
		{
			min_data = q->trees[i]->element;
		}
	}
	return min_data;
}
BinTree combineTrees(BinTree bt1, BinTree bt2)//合并两课大小相同的树，要保持堆序性
{
	if (bt1->element>bt2->element)
	{
		return combineTrees(bt2, bt1);
	}
	bt2->next_sibling = bt1->left_child;
	bt1->left_child = bt2;
	return bt1;
}
BinQueue merge(BinQueue q1, BinQueue q2)
{
	BinTree t1, t2, combined = nullptr;//二项队列高度相同的子树t1，t2和前面合成的树combined
	if (q1->current_size+q2->current_size>CAPACITY)
	{
		cerr << "merge would exceed capacity" << endl;
		return nullptr;
	}
	q1->current_size += q2->current_size;
	for (int i=0,j=1;j<=q1->current_size;++i,j*=2)//第i棵树有2^i个节点，节点数作为循环停止的条件
	{
		t1 = q1->trees[i];
		t2 = q2->trees[i];
		switch (!!t1+2*!!t2+4*!!combined)
		{
		case 0://都为空
		case 1://只有t1不为空
			break;
		case 2://只有t2不为空
			q1->trees[i] = t2;
			q2->trees[i] = nullptr;
			break;
		case 3://t1,t2不为空
			combined = combineTrees(t1, t2);
			q1->trees[i] = nullptr;
			q2->trees[i] = nullptr;
			break;
		case 4://t1,t2为空，combined不为空
			q1->trees[i] = combined;
			combined = nullptr;
			break;
		case 5://t1,combined不为空
			combined = combineTrees(t1, combined);
			q1->trees[i] = nullptr;
			break;
		case 6://combined和t2不为空
			combined = combineTrees(t2, combined);
			q2->trees[i] = nullptr;
			break;
		case 7://都不为空
			q1->trees[i] = combined;//~~~~~
			combined = combineTrees(t1, t2);//combined=combineTrees(t2,combined);
			q2->trees[i] = nullptr;
			break;
		}
	}
	return q1;
}
int isEmpty(BinQueue q)
{
	return q->current_size == 0;
}
int IsFull(BinQueue q)
{
	return q->current_size == CAPACITY;
}

test.cpp

#include "stdafx.h"
#include "BinQueue.h"
#include
int main()
{
	BinQueue q = initialize();
	ElementType input;
	cin >> input;
	while (input!=-1)
	{
		q = insertX(q, input);
		cin >> input;
	}
	cout <<"最小值1："<< findMin(q) << endl;
	deleteMin(q);
	cout << "最小值2：" << findMin(q) << endl;
	q = makeEmpty(q);
	cout << "最小值3：" << findMin(q) << endl;
	destroy(q);
    return 0;
}

结果：