【最大流】二分图匹配

前言

自从会了最大流都快要把匈牙利忘了。。。

链接

https://www.luogu.org/problemnew/show/P3386

大意

给定一个二分图，左边 n n 个点，右边 m m 个点，中间 v v 条边，求其最大匹配

思路

最大流求最大匹配，首先我们知道二分图是这样的

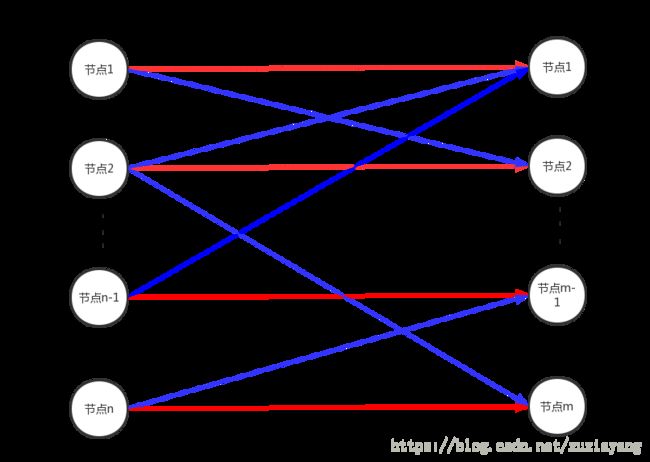
然后给它们建个源点和汇点，并把所有边的容量都调为1

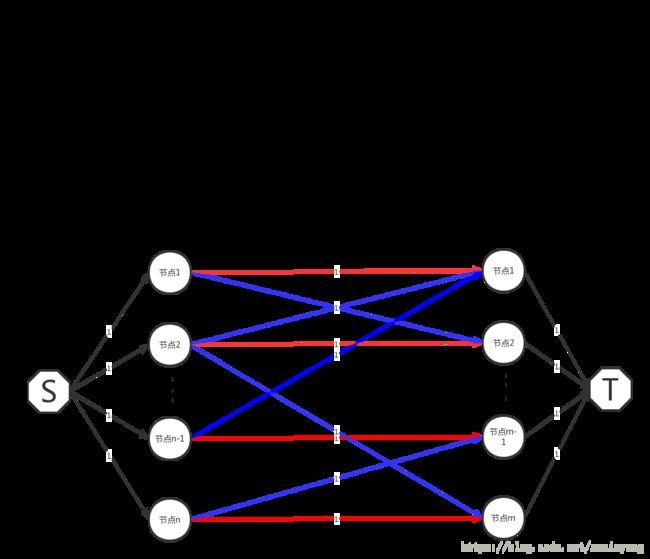
这个时候跑最大流即可

代码

#include
#include
#include
#define N 3500001
using namespace std;int m,n,v,f,s,t,sum,k;char c;
struct node{int next,to,w;}e[N<<1];
int l[N],tot,d[N];
int read()
{
    f=0;
    while (c=getchar(),c<=47||c>=58);f=(f<<3)+(f<<1)+c-48;
    while (c=getchar(),c>=48&&c<=57) f=(f<<3)+(f<<1)+c-48;
    return f;
}
void add(int u,int v,int w)
{
    e[tot]=(node){l[u],v,w};l[u]=tot++;
    e[tot]=(node){l[v],u,0};l[v]=tot++;
    return;
}
bool bfs()
{
    memset(d,-1,sizeof(d));
    queue<int>q;d[s]=0;q.push(s);
    while(q.size())
    {
        int x=q.front();q.pop();
        for(int i=l[x];~i;i=e[i].next)
        {
            int y=e[i].to;
            if(e[i].w&&d[y]==-1)
            {
                d[y]=d[x]+1;
                q.push(y);
                if(y==t) return true;
            }
        }
    }
    return false;
}
int dfs(int x,int flow)
{
    if(x==t||!flow) return flow;
    int rest=0,k=0;
    for(int i=l[x];~i;i=e[i].next)
    {
        int y=e[i].to;
        if(d[x]+1!=d[y]||!e[i].w)continue;
        f=dfs(y,min(flow-rest,e[i].w));
        if(!f) {d[y]=-1;continue;}
        e[i].w-=f;rest+=f;e[i^1].w+=f;
        if(rest==flow) return flow;
    }
    return rest;
}
void dinic()
{
    while(bfs()) sum+=dfs(s,1e9);return;
}
int main()
{
    memset(l,-1,sizeof(l));
    n=read();m=read();v=read();s=0;t=n+n+m+1;
    for(int i=1;i<=n;i++) add(s,i,1);
    for(int i=1;i<=m;i++) add(i+n,t,1);
    for(int i=1,x,y;i<=v;i++)
     x=read(),y=read(),add(x,y+n,1);
    dinic();
    printf("%d",sum);
}