八大排序总结（5）——归并排序（Merge Sort）（c语言实现）

>>>八大排序总结（1）——冒泡排序（Bubble Sort）（c语言实现）<<<

>>>八大排序总结（2）——选择排序（Selection Sort）（c语言实现）<<<

>>>八大排序总结（3）——插入排序（Insertion Sort）（c语言实现）<<<

>>>八大排序总结（4）——快速排序（Quick Sort）（c语言实现）<<<

>>>八大排序总结（6）——希尔排序（Shell Sort）（c语言实现）<<<

>>> 八大排序总结（7）——堆排序（Bubble Sort）（c语言实现）<<<

>>>八大排序总结（8）——线性时间复杂度的排序（桶排序，基数排序，计数排序）【用空间换时间】（c语言实现）<<<

>>>八大排序 时间复杂度，空间复杂度，稳定性的比较<<<

---

目录

归并排序（Merge Sort）基本思想

原理

时间，空间复杂度与算法稳定性 

代码+分析 

---

归并排序（Merge Sort）基本思想

采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

---

原理

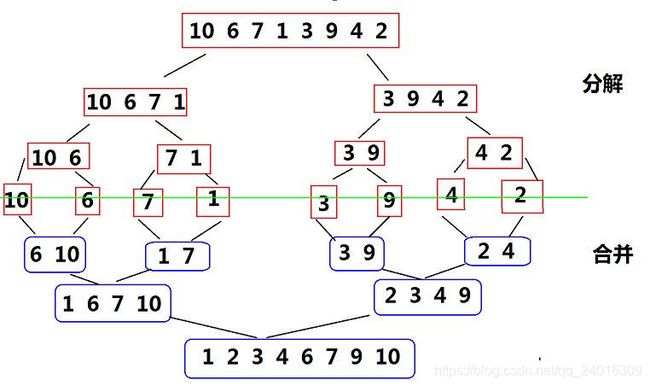
先将原序列分成两个子序列，对两个子序列进行排序，排好后再合成一个序列；在分别对子序列进行排序的时候，对每个子序列又递归用这种分而治之的方法进行排序 ，递归到只剩下两个数比较大小为止，最后再合并成一个序列。

 

---

时间，空间复杂度与算法稳定性

1.时间复杂度：

最坏情况下时间复杂度：O(NlogN)

平均时间复杂度:O(NlogN)

2.空间复杂度：O(N)

3.稳定性：稳定

 

---

代码+分析

void merge(int arr[], int low, int mid, int high)
{
    int i, k;
    int *tmp = (int *)malloc((high-low+1)*sizeof(int));
    //申请空间，使其大小为两个
    int left_low = low;
    int left_high = mid;
    int right_low = mid + 1;
    int right_high = high;

    for(k = 0; left_low <= left_high && right_low <= right_high; k++)
    {  // 比较两个指针所指向的元素
        if(arr[left_low] < arr[right_low])
        {//此处为从小到大，若要从大到小，把<改成>即可
            tmp[k] = arr[left_low++];
        }
        else
        {
            tmp[k] = arr[right_low++];
        }
    }

    if(left_low <= left_high)
    {  //若第一个序列有剩余，直接复制出来粘到合并序列尾
    //memcpy(tmp+k, arr+left_low, (left_high-left_low+l)*sizeof(int));
    for(i=left_low; i <= left_high; i++)
        tmp[k++] = arr[i];
    }

    if(right_low <= right_high)
    {
    //若第二个序列有剩余，直接复制出来粘到合并序列尾
    //memcpy(tmp+k, arr+right_low, (right_high-right_low+1)*sizeof(int));
        for(i = right_low; i <= right_high; i++)
            tmp[k++] = arr[i];
    }

    for(i = 0; i < high-low+1; i++)
        arr[low+i] = tmp[i];
    free(tmp);
}

void merge_sort(int arr[], int first, int last){
    int mid = 0;
    if(first> 1);
        merge_sort(arr, first, mid);
        merge_sort(arr, mid+1,last);
        merge(arr,first,mid,last);
    }
}

---

欢迎大家评论指正，谢谢◕‿◕