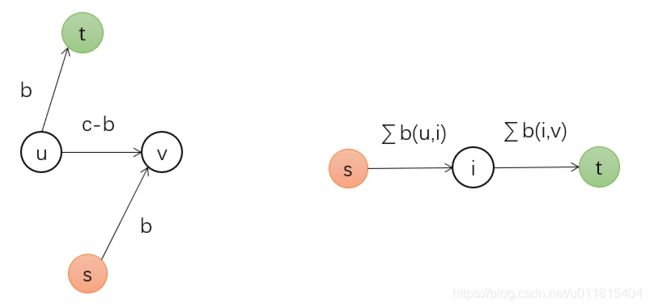图论 —— 网络流 —— 基本概念与建模技巧

【基本概念】

1.网络流

给定一个有向图 G=(V,E)，在这个图中：

• 有唯一的一个源点 S（入度为 0，出发点）
• 有唯一的一个汇点 T（出度为 0，结束点）
• 图中的每条弧（u,v）都有一非负容量 c(u,v)

此时称图 G 为网络流图（容量网络），记为：G=(V,E,c)

简单来说，图就是一种管道，管道有最大通过流量的限制，图中的边权就是容量

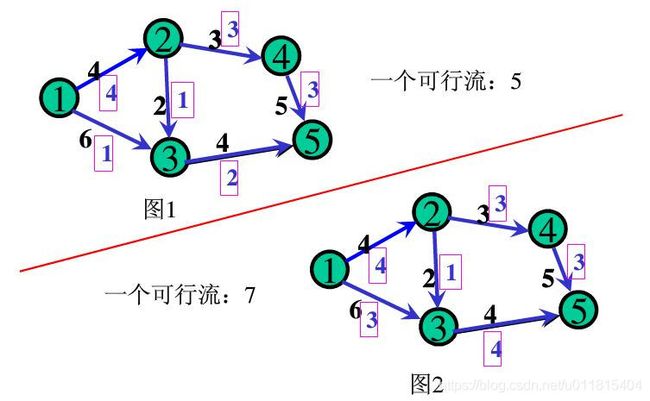
2.可行流

对于一个网络流图 G=(V,E,c)，每条弧（u,v）上给定一个实数 f(u,v)，满足：0<=f(u,v)<=c(u,v)，则称 f(u,v) 为 c(u,v) 上的流量。

若有一组流量满足：

• 源点 S 的流出量 = 整个网络的流量
• 汇点 T 的流出量 = 整个网络的流量
• 中间点的总流量 = 总流出量

那么整个网络的流量称为一个可行流（流量网络）。

此时要注意容量与流量的区别，即要注意 f(u,v) 的范围：0<=f(u,v)<=c(u,v)，不会出现流量大于容量的情况，也不会出现负流量的情况。

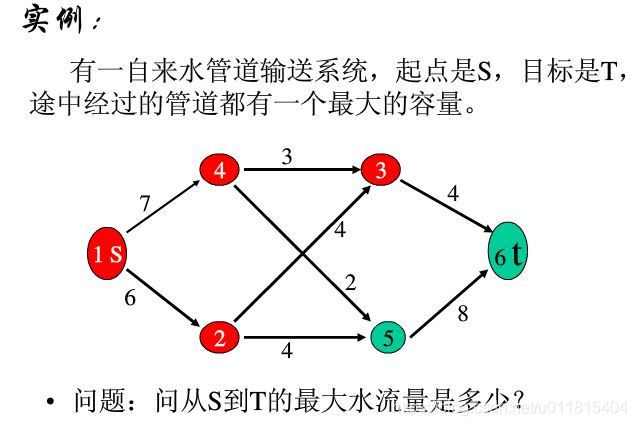
3.最大流

最大流即在所有的可行流中，流量最大的一个流量。

要注意的是，最大流可能不止一个。

在最大流问题中，任意时刻容量 c 与流量 f 满足三个性质：

• 容量限制：f(u,v) ≤ c(u,v)
• 斜对称性：f(u,v) = -f(v,u)，即从 u 到 v 的流量一定是从 v 到 u 的流量的反值。
• 流量守恒：对除 S、T 外的任意结点 u，，即：u 到相邻节点的流量之和为 0，因为流入 u 的流量和流出 u 的流量相等，u 点本身不会制造、消耗流量。

4.弧与链

1）弧的划分：在容量网络 G(V, E) 中, 设有一可行流 f={f(u,v)}，根据每条弧上流量的多少、流量和容量的关系，可将弧分四种类型：

• 饱和弧：f(u,v)=c(u,v)
• 非饱和弧：f(u,v)
• 零流弧：f(u,v)=0
• 非零流弧：f(u,v)>0

2）链：在容量网络中，称顶点序列 (u,u1,u2,…,un,v) 为一条链，要求相邻两个顶点之间有一条弧，如： 或  为容量网络中一条弧。沿着 Vs 到 Vt 的一条链, 各弧可分为两类：

• 前向弧：方向与链的正方向一致的弧，其集合记为：P+
• 后向弧：方向与链的正方向相反的弧，其集合记为：P-

5.残留容量与残留网络

1）残留容量：给定容量网络 G(V, E) 及可行流 f，弧  上的残留容量记为 c′(u,v) = c(u,v) – f(u,v)。

每条弧的残留容量表示该弧上可以增加的流量，由于从顶点 u 到顶点 v 流量的减少，等效于顶点 v 到顶点 u 流量增加，因此每条弧  上还有一个反方向的残留容量 c′(v,u) = -f(u,v)

简单来说，一个容量网络中还可以压入的流量，即每条边上的容量与流量的差称为残留容量。

2）残留网络：给定容量网络 G(V, E) 及其上的网络流 f，G 关于 f 的残留网络记为 G'(V', E')，其中 G’ 的顶点集 V’ 和 G 的顶点集 V 相同，即 V’ = V，对于 G 中的任何一条弧 ，如果 f(u,v) < c(u,v)，那么在 G’ 中有一条弧 ∈E'，其容量为 c′(u,v) = c(u,v) – f(u,v)，如果 f(u,v)>0，则在 G’ 中有一条弧 ∈E'，其容量为 c′(v,u) = f(u,v)

简单来说，由残留的容量以及源点汇点构成的网络就是残留网络。

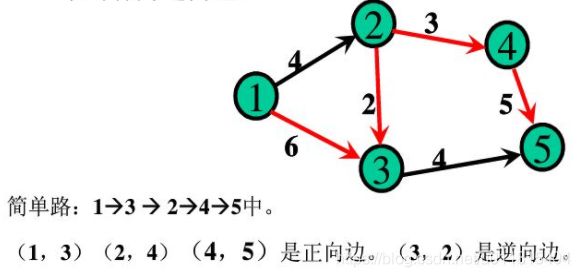
6.增广路径

在一网络中，若存在从 S 到 T 的一条简单路径，且边 (u,v) 的方向与该路径方向一致，则称 (u,v) 为正向边，否则称为逆向边。

若路径上的所有边都满足：

• 所有的正向边：f(u,v) < c(u,v)
• 所有的逆向边：f(u,v) > 0

则称该路径为一条增广路径（可增加流量）。

简单来说，增广路径，就是找到一条流量不满，未达到容量上限的一条路径，因此所有的增广路在一起便构成了残留网络。

7.割与净流量

1）割：是一种点的划分方式，对于一个网络流图 G=(V,E)，设 E' ⊆ E，若将 E' 在 G 中删除后，使得图 G 不在连通，则称 E' 是图 G 的割。割将所有的点划分为 S 和 T=V-S 两部分，记作：(S,T)

2）s-t 割：如果割所划分的两个子集使得源点 s∈S，汇点 t∈T，则该割称为 s-t 割，其中弧|u∈S,v∈T 称为割的前向弧，弧 | u∈T,v∈S 称为割的反向弧。

2）割的容量：所有前向弧的容量和，即起点在 S 终点在 T 中的所有边的容量和，记作：c(S,T) = Σc(u,v) | u∈S,v∈T

3）最小割：容量网络的最小割即容量最小的割。

4）净流量：对于一个割 (S,T)，用净流量来表示穿过割 (S,T) 的流量之和，即：|f| = f(S,T) = Σf(u,v) | u∈S,v∈T

8.层次网络

层次网络，就是将原图中的点按照点到源的距离进行分层，只保留不同层之间的边的图。

构建层次网络，简单的说，就是求出每个点 u 的层次，u 的层次是从源点到该点的最短路径（这个最短路是指弧的权都为 1 的情况下的最短路），若与源点不连通，层次置为 -1

要注意的是，当网络流进行分层后，弧可能有三种情况：

1. 1) 从第 i 层指向第 i+1 层
   2) 从第 i 层指向第 i 层
   3) 从第 i 层指向第 j 层顶点，j
2. 不存在从第 i 层指向第 i+k 层的弧，k>=2
3. 并非所有的网络都能分层

【常用定理】

1.网络流流量与割的净流量之间的关系：在一个容量网络 G(V, E) 中，设其任意一个流为 f，关于 f 的任意一个割为 (S,T)，则有 f(S,T)=|f|，即：网络流的流量等于任何割的净流量

2.网络流流量与割的容量之间的关系：在一个容量网络 G(V, E) 中，设其任意一个流为 f，任意一个割为 (S, T)，则有 f(S,T) ≤ c(S,T)，即：网络流的流量小于或等于任何割的容量

3.残留网络与原网络的关系：设 f 是容量网络 G(V, E) 的可行流，f’ 是残留网络 G’ 的可行流，则 f + f’ 仍是容量网络 G 的一个可行流，其中 f + f’ 表示对应弧上的流量相加

4.最小割最大流定理：网络的最大流的流量等于最小割的容量

5.增广路定理：网络达到最大流当且仅当残留网络中没有增广路

6.几个等价命题：对于一个网络流图 G=(V,E)，其有源点 s 和汇点 t，那么下面三个条件是等价：

• 流 f 是图 G 的最大流
• 残留网络 G' 中不存在增广路
• 对于 G 的某一个割 (S,T)，有 f = C(S,T)

【模型建立与模型变换】

1.多源多汇问题

问题：源有多个，汇有多个，流可以从任意一个源流出，最终可以流向任意一个汇，总流量等于所有源流出的总流量，也等于所有汇流入的总流量。

解决：加一超级源点 S、超级汇点 T，然后从 S 向每个源引入一条有向弧，每个汇点向 T 引出一条有向弧，容量均为无穷大。

2.结点容量

问题：每个点都有一个允许通过的最大流量，称为结点容量。

解决：将每个原始结点 u 分成 u1、u2 两个结点（一般将编号改为：u1=u、u2=u+n），中间连一有向弧，令弧的容量等于 u 的结点容量。原先到达 u 的弧改成到达 u1，原先从 u 出发的弧改为从 u2 出发。

3.无源无汇有容量下界网络的可行流

问题：无源无汇且每条弧除有容量上界 c 外，还有一个容量下界 b（原始最大流问题中的容量下界为 0，故零流即是可行流）

解决：由于无源无汇，因此所有结点都满足  "入流=出流 " 这个平衡条件。

可以建立附加源 S 与附加汇 T，然后对弧 u->v 进行改造，即添加弧 u-T> 与弧 S->v 设容量为无穷大，并将每条下界为 b 弧拆为 3 条，再进行合并，最后求改造后的网络的 S-T 最大流即可。

要注意的是，当且仅当所有附加弧满载时，原网络有可行流。

4.有容量下界网络的 S-T 最大/小流

问题：容量同时有上下界，且源点 S 和汇点 T 各有一个，求 S->T 的最大流与最小流

解决：可先用 " 无源无汇有容量下界网络的可行流 " 的方法求出可行流，然后用传统的 S-T 增广路算法得到最大流，然后将 T 看做源点，S 看作汇点，并令反向弧的容量等于原来的容量下界，最后再运行增广路算法求出 T-S 最大流即为 S-T 最小流

要注意的是，若没有下界，最小流就是零流，即原来每条弧 u->v 的反向弧容量为 0，没有什么好求的。

5.费用与流量平方成正比的最小流

问题：容量 c 均为整数，且每条弧有一个费用系数 a，表示该弧流量为 x 时费用为 ax^2，求最小费用最大流

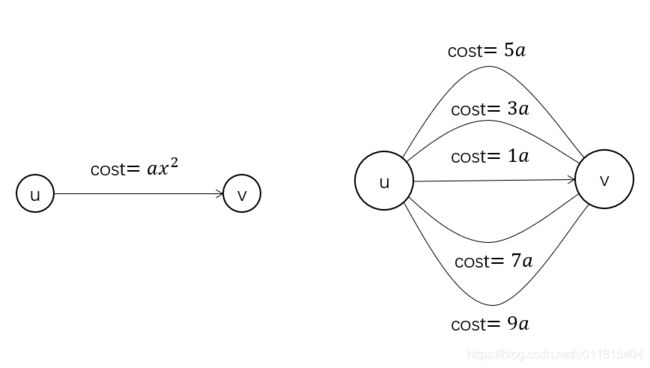
解决：使用拆边法，如下图所示，将费用系数为 a 容量为 5 的边进行拆分，拆成 5 条容量为 1 费用各异的弧

由于求的是最小费用流，如果这条弧的流量为 1，则走的肯定是 cost=1 的弧；如果流量为 2，则走的肯定是 cost=1 与 cost=3 的弧；如果流量为 3，则走的是 cost=1、cost=3、cost=5 的三条弧。可以验证，无论流量是 1~5 的哪一个，左右两个图都是等价的，这样问题就转为普通的最小费用最大流问题。

要注意的是，由于有重边，普通的邻接矩阵无法满足，因此要么使用邻接表实现，要么将邻接矩阵加一维，表示某两点间的第几条弧。

6.流量不固定的 S-T 最小费用流

问题：如果网络中的费用有正有负，且流量不固定，求最小费用流。

解决：如果费用都是正的，那么显然最小费用流就是零流。由于费用存在负值，那么最短增广路的权值就是负的，这样增广后可能得到更小的费用。

最小费用类似一下凸函数，费用随着流量增大先减小，再增大，由于三分的效率较低，因此可随着增广的进行，当增广路的权值逐渐增大最后变为正数时，停止增广。

【建模技巧】

网络流的问题难点在于模型的建立。建立模型时，一般根据题意建立一个最直观的模型，然后再用合并边、合并点、拆点等思想去简化模型，最后得出一个有效的模型。

当要求删边后再进行询问最大、最小值时，问题可以转化为求最小割

当询问是否存在不相交路径时，一般可采用最大流来解决，其核心是用拆点来使得每个点只能走一次，若路径带权，那么问题可转化为求最小费用最大流

合并边、合并点的常见规律有：

• 若几个结点的流量的来源完全相同，则可以把它们合并成一个
• 若几个结点的流量的去向完全相同，则可以把它们合并成一个
• 若从点 u 到点v有一条容量为 ∞ 的边，并且点 v 除了点 u 以外没有别的流量来源，则可以把这两个结点合并成一个