用Mixed Integer Programming做神经网络的鲁棒性验证

Evaluating Robustness of Neural Networks with Mixed Integer Programming

 

# Remarks

Conference: ICLR 2019

Full Paper: https://groups.csail.mit.edu/robotics-center/public_papers/Tjeng17.pdf

 

# Abstract

Neural networks trained only to optimize for training accuracy can often be fooled by adversarial examples—slightly perturbed inputs misclassified with high confidence. The verification of networks enables us to gauge their vulnerability to such adversarial examples. We formulate the verification of piecewise-linear neural networks as a mixed-integer program. On a representative task of finding minimum adversarial distortions, our verifier is two to three orders of magnitude quicker than the state-of-the-art. We achieve this computational speedup via tight formulations for non-linearities, as well as a novel resolve algorithm that makes full use of all information available. The computational speedup allows us to verify properties on convolutional and residual networks with over 100,000 ReLUs—several orders of magnitude more than networks previously verified by any complete verifier. In particular, we determine for the first time the exact adversarial accuracy of an MNIST classifier to perturbations with bounded l1 norm = 0:1: for this classifier, we find an adversarial example for 4.38% of samples, and a certificate of robustness to norm-bounded perturbations for the remainder. Across all robust training procedures and network architectures considered, and for both the MNIST and CIFAR-10 datasets, we are able to certify more samples than the state-of-the-art and find more adversarial examples than a strong first-order attack.

 

# Summary

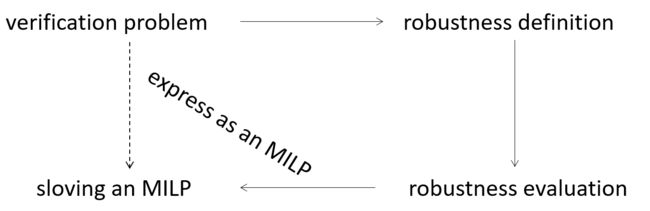
这篇文章硏究的是神经网络的验证问题。神经网络验证问题都是在有界输入的范围内，研究其输出满足的性质。这篇文章的思路是，定义分段线性神经网络的鲁棒性，将评估其鲁棒性表示为MILP问题进行求解，从而达到验证的目的。同时通过严格的非线性公式和预求解算法来加快计算速度，从而可以验证十万个Relu节点的卷积网络的属性，并且能比现有技术证明更多的样本蛤发现更对抗性示例。

 

首先看一下文章怎么定义鲁棒的。G(x)是允许扰动的区域，Xvmlid是有效输入域，fi(x')是输入X’的第i个输出，lemda(x)是真实标签。鲁棒性定义为任意一个有效的被扰动的输入，如果其输出最大值(或者范围)是真实标签，那么我们说这个网络是鲁棒的。 （这里讲一下为什么是最大值，以SHERLOCK文章里的图为例，对MNIST图像扰动一下作为输入输出有十个标签” 0-9,每个标签有一个范围”我们取最大的范围作为他预测的label。）反过来说，就是如果有另外的标签小其输出值比真实标签的输出要大，说明网络分类错误，那么这个网络就是不鲁棒的。所以这样的输入就是一个对抗性示例。

文章提出两个用于实验的指标。 第一个是对抗准确度，用于测试集。测试集的每个样本作为输入验证成功的样本除以总样 本数就是对抗准确度。 第二个是最小对抗失真。它指的是有效输入域中，真实标签的输入x和最接近真实标签的标 签的输入x之间的距离。

 

接下来我们看一下网络的约束生成。首先输入的约束是G(x)，受扰动的输入域距离原始输入在一个无穷范式距离epsilon范围内。可以想象成一个半径为epsilon的球。作者总是在第一层用区间算术来计算输出，也就是乘权重加上误差。这样可以快速确定粗略的边界，然后使用具有较高计算复杂性的过程来精简边界。作者把网络看作一个图G，有向边从函数输入指向输出，顶点表示变量。源节点对应于网络的输入，汇聚节点对应于网络输出。以计算某个变量v为例，可以只关注以v为根的子图。计 算v的上界只需要在子图对应的MILP问题Mv中，最大化对应的值.计算下界同理。(附录 中提到两种减少计算时间的方法，用凸松弛来放宽整数约束)。

另外作者说明了在激活处的MILP制定方法。以ReLU为例：区间计算之后传给激活函数的范围有三种情况。上界小于0和下界大于0的情况比较简单。当上界大于0下界小于0时，MILP制定为一些性质的析取。这里作者引入一个指示决策变量比当取值在非激活部分， a为0，在激活部分a为1。根据 ReLU的性质，我们可以直接得到两条约束。引入变量的约束可以这样理解： （1）当激活的时候，a=1,前两条约束是更紧的，并且知道激活的时候y=x,已经有y>=x,所以第一条约束应为y<=x,所以引入变量s的部分应为0。 （2）当非激活的时候，a=0,后两条约束是更紧的”并且知道这时候y=0,已经有y>=0，所以第三条约束应为y<=0。 这个就是制定ReLU的MILP过程。

[算法]作者写了算法说明制定ReLU的MILP过程。 fs是确定ReLU节点边界的过程，首先初始化上下界，接着循环，执行渐进式紧缩过程，也 就是区间算术”将计算后的上界与原来的比较，替换另较小的值。宓后判断上界是否』吁0 ，小于0就是上一张PPT的第一种周兄y=0ₒ然后计算下界”下界大于0就是第三种情况， y=x,否则的话就是第二种情况。

[实验] 数据集：MNIST和CIFAR-10 网络结构：FNN （MLP、CNN、ResNet） 第一个实验是作者提出的验证器的性能测试，也就是本文方法的运行时间。任务是确定MNIST分类器LPd-CNNA对loo范数约束e=0.1的扰动的对抗精度。建立时间是指用于确定界限的时间，而求解时间是指在确定所有界限后用于解决公式2中主要MILP问题的时间。（探索的节点可能指的是每个MILP问题中有关的节点数）Using restricted input domain （受限输入域）指的是初始化输入域的过程。Progressive tightening （渐进式紧缩）指的是第一层的区间算术。Using asymmetric bounds （不对称边界）指的是制定ReLU约束组。

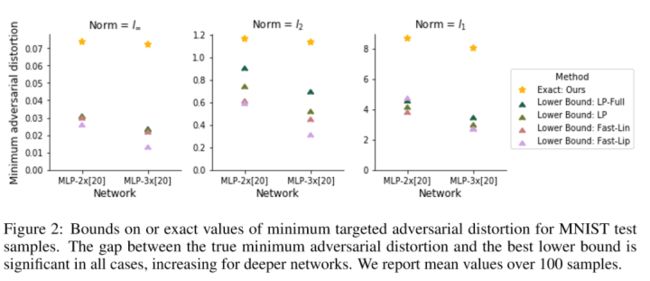
然后与其他验证器的时间上的比较（对Reluplex和LP, Fast-Lip, Fast・Lin和LP-full）Reluplex是完备的验证器，能找到确定的最小对抗失真。其他的都不是完备的，只能提供最小失真的下限。结果表明在loo范数扰动上，将Reluplex的速度提高了2到3个数量级。

然后是最小对抗失真的界限和确切值的比较。

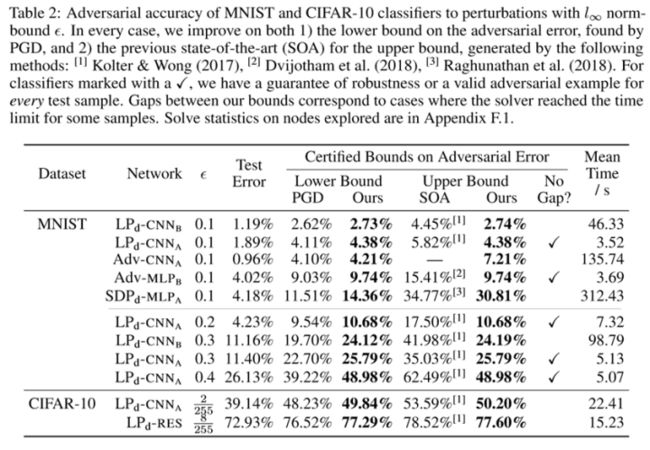
第二个实验是确定对抗精度表2列出了这些分类器的测试误差和对抗误差的估计值。MLPa: 1*[500] MLPb: 2*[200] CNN和ResNet不多赘述，文章有介绍。用本文的方法和其他方法比较了对抗误差。 对于标有勾的分类器”我们可以保证每个测试样本的鲁棒性或有效的对抗性示例。可以看出改进了由PGD找到的对抗性误差的下限和先前最新技术生成的对抗误差的上限。