阵列天线方向图-均匀圆形/圆柱阵列matlab仿真

均匀圆形阵列

圆阵：各个天线阵元排列成一个圆环
优点：提供$360^{\circ }$方位角；在天线扫描过程中能基本维持天线波束形状和天线增益
缺点：耗用较多的阵元；旁瓣电平较高

建立一个半径为$R=k\cdot \lambda$的圆形阵列模型，均匀排布着$M$个天线阵元。第$m$个阵元和圆心$O$之间的连线与$x$轴的夹角为${\gamma }_m=2\pi m/M$，则位置向量表达式为
$${P\text{P}P}_m=(R\cos {\gamma }_m,R\sin {\gamma }_m,0)$$

波达方向矢量为
$$r\text{r}r=(\sin \theta \cos \varphi ,\sin \theta \sin \varphi ,\cos \theta )$$

同一时刻，原点与阵元$m$接收到的信号包络之间的相位差为
$$\begin{array}{rl}\Delta {\psi }_m& =\frac{2\pi }{\lambda }r\text{r}r\cdot {P\text{P}P}_m\\ & =\frac{2\pi }{\lambda }R\sin \theta \cos (\varphi -{\gamma }_m)\end{array}$$

设阵列主波束的最大值指向为$({\varphi }_0,{\theta }_0)$，第$m$个阵元的激励幅度和相位分别是$A_m$和${\alpha }_m$，则有
$${\alpha }_m=-\frac{2\pi }{\lambda }R\sin {\theta }_0\cos ({\varphi }_0-{\gamma }_m)$$

综上，方向图函数可以表示为
$$F(\varphi ,\theta )=\sum _{m=0}^{M-1}{A}_m{e}^{j(\Delta {\psi }_m-{\alpha }_m)}\cdot f_m(\varphi ,\theta )$$

假设天线阵元方向图$f_m(\varphi ,\theta )$满足全向性，在线阵天线波束扫面范围内，可忽略其影响，即$f_m(\varphi ,\theta )=1$；天线照射口径函数等幅分布，幅度加权系数$A_m=1$，满足均匀分布，则上式可简化为
$$F(\varphi ,\theta )=\sum _{m=0}^{M-1}{e}^{j\frac{2\pi }{\lambda }R[\sin \theta \cos (\varphi -{\gamma }_m)-\sin {\theta }_0\cos ({\varphi }_0-{\gamma }_m)]}$$

用MATLAB仿真：
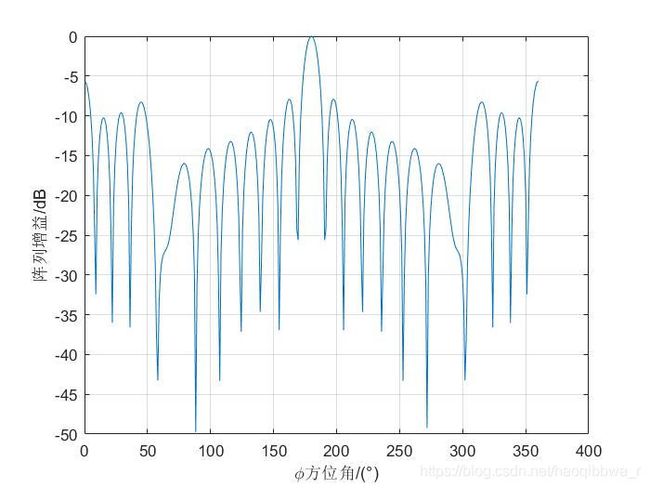
设一均匀圆形阵列，阵列半径$R=5\lambda$，阵列上均匀分布了62个天线阵元，所有阵元等幅全向，两阵元的之间距离约为$\lambda /2$，天线波束指向为$(180^{\circ },45^{\circ })$。

均匀圆柱阵列

共形阵列天线：若将雷达天线的各个阵元安装在雷达平台的表面上，使阵列天线的表面与雷达平台外形吻合
圆柱阵列：如果将多个圆阵平行分布在一个圆柱体上，便可构成圆柱阵列，圆柱阵列是最简单的共形阵列

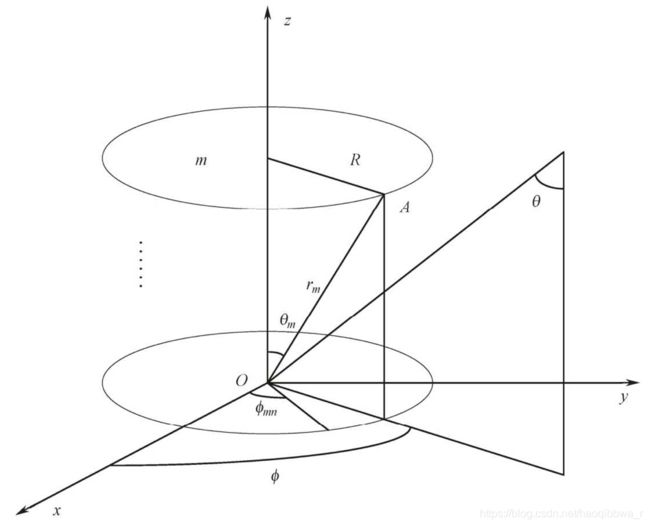
设一个圆柱阵列由$M$个半径为$R$的圆形阵列组成，每个圆上均匀分布着$N$个阵元。所有圆上的阵元分不对称，方位角相等。第$m=0,1,\cdots ,M-1$个圆与下底面之间的距离为$h_m$。点$A$为第$m$个平面圆上的某一阵元，在圆上均匀分布的方位角为${\varphi }_{mn}$，俯仰角为
$${\theta }_m=\arctan (R/h_m)$$

且
$$r_m=\sqrt{R^2+h_m^2}$$

$r\text{r}r$表示参考点$O$到阵元$A$的向量，${R\text{R}R}_0$为参考点$O$到远场目标方向的单位向量。$r\text{r}r$的坐标为$(R\cos {\varphi }_{mn},R\sin {\varphi }_{mn},h_m)$，${R\text{R}R}_0$的坐标为$(\sin \theta \cos \varphi ,\sin \theta \sin \varphi ,\cos \theta )$，则阵元$A$相对于参考点$O$到远场目标的相对相位为
$${\beta }_{mn}=\frac{2\pi }{\lambda }(r\text{r}r\cdot {R\text{R}R}_0)$$

当$m=0$时，表示底面圆环，此时$h=0$，$r_m=R$，${\theta }_m=\frac{\pi }{2}$，则底面圆弧上阵元$n$相对于参考点$O$的相位差为
$${\beta }_{0n}=\frac{2\pi }{\lambda }{R}_0\sin \theta \cos (\varphi -{\varphi }_{0n})$$

当$m=1,2,\cdots ,M-1$时，各圆阵上阵元$n$相对于参考点$O$的相位差为
$${\beta }_{mn}=\frac{2\pi }{\lambda }{r}_m[\sin {\theta }_m\sin \theta \cos (\varphi -{\varphi }_{mn})+\cos {\theta }_m\cos \theta ]$$

所有$M$个圆形阵列天线上所有阵元形成的总的阵列方向图函数为
$$F(\varphi ,\theta )=\sum _{m=0}^{M-1}\sum _{n=0}^{N-1}{f}_{mn}(\varphi ,\theta )A_{mn}\exp \{j[\frac{2\pi }{\lambda }{r}_m(\sin {\theta }_m\sin \theta \cos (\varphi -{\varphi }_{mn})+\cos {\theta }_m\cos \theta )-{\psi }_{mn}]\}$$

$f_{mn}(\varphi ,\theta )$为阵元方向图，$A_{mn}$为幅度加权系数，${\psi }_{mn}$为相应阵元的初始相位差，为了使主波束能指向$({\varphi }_0,{\theta }_0)$方向，则有
$${\psi }_{mn}=\frac{2\pi }{\lambda }{r}_m[\sin {\theta }_m\sin {\theta }_0\cos ({\varphi }_0-{\varphi }_{mn})+\cos {\theta }_m\cos {\theta }_0]$$

方向图函数为
$$F(\varphi ,\theta ;{\varphi }_0,{\theta }_0)=\sum _{m=0}^{M-1}\sum _{n=0}^{N-1}{f}_{mn}(\varphi ,\theta )A_{mn}\exp \{j\frac{2\pi }{\lambda }{r}_m[(\sin {\theta }_m(\sin \theta \cos (\varphi -{\varphi }_{mn})-\sin {\theta }_0\cos ({\varphi }_0-{\varphi }_{mn}))+\cos {\theta }_m(\cos \theta -\cos {\theta }_0)]\}$$

假设天线阵元方向图$f_{mn}(\varphi ,\theta )$满足全向性，在线阵天线波束扫面范围内，可忽略其影响，即$f_{mn}(\varphi ,\theta )=1$；天线照射口径函数等幅分布，幅度加权系数$A_{mn}=1$，满足均匀分布，则上式可简化为
$$F(\varphi ,\theta ;{\varphi }_0,{\theta }_0)=\sum _{m=0}^{M-1}\sum _{n=0}^{N-1}\exp \{j\frac{2\pi }{\lambda }{r}_m[(\sin {\theta }_m(\sin \theta \cos (\varphi -{\varphi }_{mn})-\sin {\theta }_0\cos ({\varphi }_0-{\varphi }_{mn}))+\cos {\theta }_m(\cos \theta -\cos {\theta }_0)]\}$$

用MATLAB仿真：
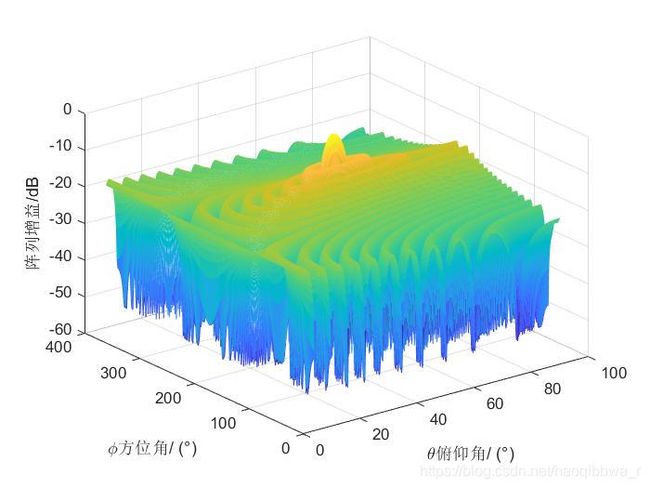
设一均匀圆柱阵列，阵列半径$R=2\lambda$，高度$H=9.5\lambda$。阵元按间隔$\lambda /2$均匀排布，每个圆环上排布24个天线阵元，共排布20个阵圆环，所有阵元等幅全向，天线波束指向为$(180^{\circ },90^{\circ })$。