算法导论 — 7.4 快速排序分析
笔记
本节给出快速排序运行时间的详细分析。
(1) 最坏情况运行时间
假设 T ( n ) T(n) T(n)是最坏情况下QUICKSORT的运行时间,那么 T ( n ) T(n) T(n)满足以下递归式
![]()
因为调用PARTITION生成的2个子数组的长度加起来为 n − 1 n-1 n−1,因此上式中参数 q q q的变化范围是 0 n − 1 0 ~ n-1 0 n−1。我们用代入法来证明 T ( n ) = Θ ( n 2 ) T(n) = Θ(n^2) T(n)=Θ(n2)。
先证明 T ( n ) = O ( n 2 ) T(n) = O(n^2) T(n)=O(n2)。假设 T ( n ) ≤ c n 2 T(n) ≤ cn^2 T(n)≤cn2,其中 c c c为一个常数。
我们先看初始情况 n = 1 n = 1 n=1。此时有 T ( 1 ) = 2 T ( 0 ) + Θ ( 1 ) T(1) = 2T(0) + Θ(1) T(1)=2T(0)+Θ(1)。 T ( 0 ) T(0) T(0)为常数时间,显然只要 c c c足够大,就能使得 T ( 1 ) = 2 T ( 0 ) + Θ ( 1 ) ≤ c • 1 2 T(1) = 2T(0) + Θ(1) ≤ c•1^2 T(1)=2T(0)+Θ(1)≤c•12成立。
现在进行数学归纳。假设 T ( n ) ≤ c n 2 T(n) ≤ cn^2 T(n)≤cn2对 1 , 2 , … , n − 1 1, 2, …, n-1 1,2,…,n−1都成立。于是有

在 q ∈ [ 0 , n − 1 ] q ∈ [0, n-1] q∈[0,n−1]范围内,表达式 q 2 + ( n − q − 1 ) 2 q^2+(n-q-1)^2 q2+(n−q−1)2在 q = 0 q = 0 q=0或 q = n − 1 q = n-1 q=n−1时取得最大值,并且最大值为 ( n − 1 ) 2 (n-1)^2 (n−1)2。因此
![]()
如果 c c c足够大,使得 c ( 2 n − 1 ) c(2n-1) c(2n−1)大于 Θ ( n ) Θ(n) Θ(n),就可以使得 T ( n ) ≤ c n 2 T(n) ≤ cn^2 T(n)≤cn2成立。
综上所述,只要选取足够大的 c c c,就可以使得 T ( n ) ≤ c n 2 T(n) ≤ cn^2 T(n)≤cn2对所有 n n n的取值都成立。因此, T ( n ) = O ( n 2 ) T(n) = O(n^2) T(n)=O(n2)成立。
我们同样可以证明 T ( n ) = Ω ( n 2 ) T(n) = Ω(n^2) T(n)=Ω(n2)(见练习7.4-1)。因此,快速排序的最坏情况运行时间为 Θ ( n 2 ) Θ(n^2) Θ(n2)。
(2) 期望运行时间
快速排序的运行时间实际上取决于元素之间比较的次数,我们假设总的比较次数为 X X X。我们假设一个数组 Z Z Z中的元素从小到大依次为 z 1 , z 2 , … , z n z_1, z_2, …, z_n z1,z2,…,zn,并用 Z i j Z_{ij} Zij表示 z i z_i zi与 z j z_j zj之间的元素集合 z i , z i + 1 , … , z j {z_i, z_{i+1}, …, z_j} zi,zi+1,…,zj。我们要考察任意 2 2 2个元素 z i z_i zi与 z j z_j zj什么时候会进行比较。
首先我们可以断言,每一对元素至多比较一次。因为在PARTITION调用过程中,每个元素只会与选出来的划分主元进行比较,并且比较结束后,这个被选出来的划分主元就会被放置到正确的位置,在之后递归调用PARTITION过程中,这个划分元素就不会再参与比较了。
我们用 X i j X_{ij} Xij表示元素 z i z_i zi与 z j z_j zj的比较次数。根据上面的分析, X i j X_{ij} Xij是一个随机变量,并且只可能有 2 2 2个取值: 0 0 0和 1 1 1。换言之, X i j X_{ij} Xij是一个指示器随机变量。
![]()
由随机变量 X i j X_{ij} Xij,我们可以很容易得到总的比较次数

我们要计算快速排序的期望运行时间,也就是要计算总的比较次数 X X X的期望值 E [ X ] E[X] E[X],于是有

其中 P r Pr Pr{ z i z_i zi与 z j z_j zj进行比较} 是 z i z_i zi与 z j z_j zj进行比较的概率。
我们现在来分析任意 2 2 2个元素 z i z_i zi与 z j z_j zj会进行比较的概率。我们假设数组中每个元素都是互异的。如果在包含 Z i j Z_{ij} Zij中的所有元素的一次PARTITION调用中,一旦满足 z i < x < z j z_i < x < z_j zi<x<zj的一个元素 x x x被选择为划分主元,那么 z i z_i zi和 z j z_j zj就会划分到2个不同的子数组中, z i z_i zi和 z j z_j zj就再也没有机会进行比较了。相反地,如果在包含 Z i j Z_{ij} Zij中的所有元素的一次PARTITION调用中, z i z_i zi被选为划分主元,那么 z i z_i zi就会和 z j z_j zj比较;同样,如果 z j z_j zj被选为划分主元,那么 z i z_i zi也会和 z j z_j zj比较。因此,当且仅当 z i z_i zi或 z j z_j zj在 Z i j Z_{ij} Zij中被首先选为划分主元时, z i z_i zi和 z j z_j zj才会进行比较。 Z i j Z_{ij} Zij中的元素都会等可能地被首先选为划分主元,所以每个元素被选择的概率为 1 / ( j − i + 1 ) 1/(j-i+1) 1/(j−i+1)。于是有

于是我们可以得到

我们令 k = j − i k = j-i k=j−i,将上式做一下变换。
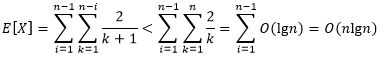
由此我们得到,快速排序的期望运行时间的上界为 O ( n l g n ) O(n{\rm lg}n) O(nlgn)。在7.2节,我们得到结论:快速排序的最好情况运行时间为 Θ ( n l g n ) Θ(n{\rm lg}n) Θ(nlgn),即快速排序的运行时间的下界为 Ω ( n l g n ) Ω(n{\rm lg}n) Ω(nlgn)。因此,我们可以断言,快速排序的期望时间复杂度为 Θ ( n l g n ) Θ(n{\rm lg}n) Θ(nlgn)。
练习
7.4-1 证明:在递归式
![]()
中, T ( n ) = Ω ( n 2 ) T(n) = Ω(n^2) T(n)=Ω(n2)。
解
假设 T ( n ) ≥ c n 2 T(n) ≥ cn^2 T(n)≥cn2,其中 c c c为一个常数。我们用数学归纳法来证明。
(1) 初始情况n = 1
此时有 T ( 1 ) = 2 T ( 0 ) + Θ ( 1 ) T(1) = 2T(0) + Θ(1) T(1)=2T(0)+Θ(1)。 T ( 0 ) T(0) T(0)为常数时间,显然只要 c c c足够小,就能使得 T ( 1 ) = 2 T ( 0 ) + Θ ( 1 ) ≥ c • 1 2 T(1) = 2T(0) + Θ(1) ≥ c•1^2 T(1)=2T(0)+Θ(1)≥c•12成立。
(2) 归纳过程
假设 T ( n ) ≥ c n 2 T(n) ≥ cn^2 T(n)≥cn2对 1 , 2 , … , n − 1 1, 2, …, n-1 1,2,…,n−1都成立,于是有
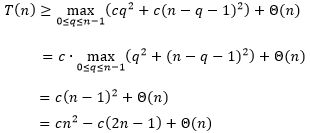
显然,只要 c c c足够小,就能使得 c ( 2 n − 1 ) 小 于 Θ ( n ) c(2n-1)小于Θ(n) c(2n−1)小于Θ(n),也就可以使得 T ( n ) ≥ c n 2 T(n) ≥ cn^2 T(n)≥cn2成立。
综上所述,只要选取足够小的 c c c,就能使得 T ( n ) ≥ c n 2 T(n) ≥ cn^2 T(n)≥cn2对所有 n n n的所有取值都成立。因此, T ( n ) = Ω ( n 2 ) T(n) = Ω(n^2) T(n)=Ω(n2)成立。
7.4-2 证明:在最好情况下,快速排序的运行时间为 Ω ( n l g n ) Ω(n{\rm lg}n) Ω(nlgn)。
解
在最好情况下,快速排序的运行时间 T ( n ) T(n) T(n)满足以下递归式
![]()
假设 T ( n ) ≥ c n l g n T(n) ≥ cn{\rm lg}n T(n)≥cnlgn,其中 c c c为一个常数。我们用数学归纳法来证明。
(1) 初始情况n = 1
此时有 T ( 1 ) = 2 T ( 0 ) + Θ ( 1 ) T(1) = 2T(0) + Θ(1) T(1)=2T(0)+Θ(1)。显然无论 c c c取何值,都能使得 T ( 1 ) = 2 T ( 0 ) + Θ ( 1 ) ≥ c • 1 • l g 1 = 0 T(1) = 2T(0) + Θ(1) ≥ c•1•{\rm lg}1 = 0 T(1)=2T(0)+Θ(1)≥c•1•lg1=0成立。
(2) 归纳过程
假设 T ( n ) ≥ c n l g n T(n) ≥ cn{\rm lg}n T(n)≥cnlgn对 1 , 2 , … , n − 1 1, 2, …, n-1 1,2,…,n−1都成立,于是有
![]()
定义函数 f ( q ) = q l g q + ( n − q − 1 ) l g ( n − q − 1 ) f(q)=q{\rm lg}q+(n-q-1){\rm lg}(n-q-1) f(q)=qlgq+(n−q−1)lg(n−q−1),其中自变量 q q q的取值范围为 [ 0 , n − 1 ] [0, n-1] [0,n−1],我们要求这个函数的最小值。对 f ( q ) f(q) f(q)求导,得到

当 q = ( n − 1 ) / 2 q = (n-1)/2 q=(n−1)/2时,有 f ′ ( q ) = 0 f'(q)=0 f′(q)=0;当 q < ( n − 1 ) / 2 q < (n-1)/2 q<(n−1)/2时,有 f ′ ( q ) < 0 f'(q)<0 f′(q)<0;而当 q > ( n − 1 ) / 2 q > (n-1)/2 q>(n−1)/2时,有 f ′ ( q ) > 0 f'(q)>0 f′(q)>0。因此, f ( q ) f(q) f(q)在 q = ( n − 1 ) / 2 q = (n-1)/2 q=(n−1)/2时取得最小值,最小值为 ( n − 1 ) l g ( ( n − 1 ) / 2 ) = ( n − 1 ) l g ( n − 1 ) − ( n − 1 ) (n-1){\rm lg}((n-1)/2)=(n-1){\rm lg}(n-1)-(n-1) (n−1)lg((n−1)/2)=(n−1)lg(n−1)−(n−1)。于是有
![]()
为了让 T ( n ) ≥ c n l g n T(n) ≥ cn{\rm lg}n T(n)≥cnlgn成立。我们令 c ( n − 1 ) l g ( n − 1 ) − c ( n − 1 ) + Θ ( n ) ≥ c n l g n c(n-1){\rm lg}(n-1)-c(n-1)+Θ(n)≥cn{\rm lg}n c(n−1)lg(n−1)−c(n−1)+Θ(n)≥cnlgn。将这个不等式变换一下,得到
![]()
由于 n l g n + n − 1 − ( n − 1 ) l g ( n − 1 ) > 0 n{\rm lg}n+n-1-(n-1){\rm lg}(n-1)>0 nlgn+n−1−(n−1)lg(n−1)>0,所以上面的不等式可以求解得到
![]()
上式说明,只要 c c c足够小,就能够使得 T ( n ) ≥ c ( n − 1 ) l g ( n − 1 ) − c ( n − 1 ) + Θ ( n ) ≥ c n l g n T(n)≥c(n-1){\rm lg}(n-1)-c(n-1)+Θ(n)≥cn{\rm lg}n T(n)≥c(n−1)lg(n−1)−c(n−1)+Θ(n)≥cnlgn成立。
综上所述,只要选取足够小的 c c c,就能使得 T ( n ) ≥ c n l g n T(n) ≥ cn{\rm lg}n T(n)≥cnlgn对所有 n n n的取值都成立。因此, T ( n ) = Ω ( n l g n ) T(n) = Ω(n{\rm lg}n) T(n)=Ω(nlgn)成立。
7.4-3 证明:在 q = 0 , 1 , … , n − 1 q = 0, 1, …, n-1 q=0,1,…,n−1区间内,当 q = 0 q = 0 q=0或 q = n − 1 q = n-1 q=n−1时, q 2 + ( n − q − 1 ) 2 q^2+(n-q-1)^2 q2+(n−q−1)2取得最大值。
解
定义函数 f ( q ) = q 2 + ( n − q − 1 ) 2 = 2 q 2 – 2 ( n − 1 ) q + ( n − 1 ) 2 f(q) = q^2+(n-q-1)^2 = 2q^2 – 2(n-1)q + (n-1)^2 f(q)=q2+(n−q−1)2=2q2–2(n−1)q+(n−1)2。这是一个二次函数,它的曲线是一个开口向上的抛物线。我们知道,抛物线 y = a x 2 + b x + c y = ax^2 + bx + c y=ax2+bx+c的顶点的 x x x坐标为 − b / 2 a -b/2a −b/2a。于是, f ( q ) f(q) f(q)的顶点横坐标为
![]()
f ( q ) f(q) f(q)在顶点 ( n − 1 ) / 2 (n-1)/2 (n−1)/2处取得最小值,并且 ( n − 1 ) / 2 (n-1)/2 (n−1)/2正好位于区间 [ 0 , n − 1 ] [0, n-1] [0,n−1]的正中间。根据抛物线的对称性,可以得出 f ( q ) f(q) f(q)在 q = 0 q = 0 q=0或 q = n − 1 q = n-1 q=n−1时取得最大值。
7.4-4 证明:RANDOMIZED-QUICKSORT期望运行时间是 Ω ( n l g n ) Ω(n{\rm lg}n) Ω(nlgn)。
略
7.4-5 当输入数据已经“几乎有序”时,插入排序速度很快。在实际应用中,我们可以利用这一特点来提高快速排序的速度。当对一个长度小于 k k k的子数组调用快速排序时,让它们不做任何排序就返回。当上层的快速排序调用返回后,对整个数组运行插入排序来完成排序过程。试证明:这一排序算法的期望时间复杂度为 O ( n k + n l g ( n / k ) ) O(nk+n{\rm lg}(n/k)) O(nk+nlg(n/k))。分别从理论和实践的角度说明我们应该如何选择 k k k?
解
该题如果要严格证明很有难度,只做简单的分析。
该算法分为快速排序阶段和插入排序阶段。为简化分析,假设快速排序阶段后,留下的还未排序的子数组长度都为 k − 1 k-1 k−1。实际上,快速排序阶段有可能会得到长度小于 k − 1 k-1 k−1的子数组,但如果要考虑这些情况的话,分析太过复杂了。
下面对2个阶段分别进行分析。
(1) 快速排序阶段
我们回想一下本节对快速排序的分析,比较次数的期望值为 ∑ i = 1 n − 1 ∑ j = i + 1 n [ 2 / ( j − i + 1 ) ] ∑_{i=1}^{n-1}∑_{j=i+1}^{n}[2/(j-i+1)] ∑i=1n−1∑j=i+1n[2/(j−i+1)]。在累加式中,下标 j j j从i+1开始,到 n n n结束。
对于本题的排序方案,在快速排序阶段,递归调用PARTITION划分到所有子数组的规模等于 k − 1 k-1 k−1为止。于是在快速排序阶段,只需要考虑长度不小于 k k k的子数组。因此,在累加式中,下标 j j j应当从 i + k − 1 i+k-1 i+k−1开始,到 n n n结束。同时,下标 i i i应当从 1 1 1开始,到 n − k + 1 n-k+1 n−k+1结束。于是,比较次数的期望值为

故快速排序阶段的期望时间复杂度为 O ( n l g ( n / k ) ) O(n{\rm lg}(n/k)) O(nlg(n/k))。
(2) 插入排序阶段
插入排序阶段虽然还是对整个数组执行插入排序,但是实际上可以看作是分别对快速排序阶段留下的每一个长度为 k − 1 k-1 k−1的子数组执行插入排序,因为子数组与子数组之间的顺序已经是正确的,只有子数组内部是还未经排序的。
长度为 k − 1 k-1 k−1的子数组不超过 n / ( k − 1 ) n/(k-1) n/(k−1)个,对每个子数组执行插入排序的期望时间复杂度为 O ( ( k − 1 ) 2 ) O((k-1)^2) O((k−1)2)。因此,对所有长度为 k − 1 k-1 k−1的子数组进行插入排序的期望时间复杂度为
![]()
综合以上两部分,得到本题提出的排序算法的期望时间复杂度为 O ( n k + n l g ( n / k ) ) O(nk+n{\rm lg}(n/k)) O(nk+nlg(n/k))。
从理论上来说, k k k的选择与两种排序算法时间复杂度中的常量因子有关。如果快速排序时间复杂度中的常量因子相比插入排序常量因子越大,那么 k k k也应当越大。反之, k k k应当越小。
实际应用中,可以通过实验来确定 k k k应当如何选择。这部分实验后期再补上。
7.4-6 考虑对PARTITION过程做这样的修改:从数组 A A A中随机选出三个元素,并用这三个元素的中位数(即这三个元素按大小排在中间的值)对数组进行划分。求以 α α α的函数形式表示的、最坏划分比例为 α : ( 1 − α ) α:(1-α) α:(1−α)的近似概率,其中 0 < α < 1 0 < α < 1 0<α<1。
解
我们不妨设定 α α α的取值范围为 0 < α ≤ 1 / 2 0 < α ≤ 1/2 0<α≤1/2。 1 / 2 < α < 1 1/2 < α < 1 1/2<α<1实际上是对称的情况。
如果数组已经排好序,可以按照元素的大小顺序将数组分为 3 3 3个部分,如下图所示。
![]()
如果PARTITION过程选择的划分主元位于第②部分,那么产生的划分比 α : ( 1 − α ) α:(1-α) α:(1−α)更好;而如果选择的划分主元位于第①部分和第③部分,那么产生的划分比 α : ( 1 − α ) α:(1-α) α:(1−α)更坏。因此,我们需要求在数组中任取 3 3 3个元素,中位数位于第②部分的概率。而中位数于第②部分,又可分为3种情况。
(1) 从第②部分任取3个元素
从第②部分 ( 1 − 2 α ) n (1-2α)n (1−2α)n个元素中任取3个,有以下这么多种取法。
![]()
(2) 从第②部分任取2个元素,从第①部分或第③部分任取1个元素
从第②部分 ( 1 − 2 α ) n (1-2α)n (1−2α)n个元素中任取2个,并且从第①部分和第③部分 2 α n 2αn 2αn个元素中任取1个,有以下这么多种取法。
![]()
(3) 从第①部分、第②部分和第③部分中各任取1个元素
从第①部分 α n αn αn个元素中任取1个,从第②部分 ( 1 − 2 α ) n (1-2α)n (1−2α)n个元素中任取1个,再从第③部分 α n αn αn个元素中任取1个,有以下这么多种取法。
![]()
而从整个数组中任取3个元素,一共有以下这么多种取法。
![]()
因此,中位数位于第②部分的概率 p p p为

这个概率与数组的规模 n n n有关。通常我们更关注 n n n比较大的情况。我们计算 n n n趋近于 ∞ ∞ ∞时,概率 p p p的极限,有
![]()
(注意:求 n → ∞ n→∞ n→∞时 p p p的极限,只需要将分子和分母中的低阶项删掉,保留高阶项即可。)
所以对规模 n n n足够大的数组,采用三数取中法,中位数位于第②部分的概率接近于 1 − 6 α 2 + 4 α 3 1-6α^2+4α^3 1−6α2+4α3。这也是应用三数取中法得到的数组划分好于 α : ( 1 − α ) α:(1-α) α:(1−α)的近似概率。
我们可以侧面检验一下这个结果的正确性。将 α = 1 / 2 α = 1/2 α=1/2代入 p p p的极限,得到
![]()
这说明“数组划分好于 1 / 2 : 1 / 2 1/2:1/2 1/2:1/2(即完全平衡划分)”是不可能出现的。显然,这符合“数组划分的最好情况就是完全的平衡划分”这一事实。
我们再做一点分析,将“三数取中法”与原始方法进行比较。原始方法是随机选择一个划分元素,只有当这个元素位于第②部分时,才能得到一个好于 α : ( 1 − α ) α:(1-α) α:(1−α)的划分,这种情况出现的概率为
![]()
我们比较 p p p与 q q q的大小,有 p − q = 1 − 6 α 2 + 4 α 3 − ( 1 − 2 α ) = 2 α ( 1 − α ) ( 1 − 2 α ) p-q=1-6α^2+4α^3-(1-2α)=2α(1-α)(1-2α) p−q=1−6α2+4α3−(1−2α)=2α(1−α)(1−2α)。显然,在 0 < α ≤ 1 / 2 0 < α ≤ 1/2 0<α≤1/2取值范围内,有 2 α ( 1 − α ) ( 1 − 2 α ) ≥ 0 2α(1-α)(1-2α)≥0 2α(1−α)(1−2α)≥0。因此,“三数取中法”较原始方法有更高的可能性得到更好的划分。