如何深入浅出的理解 Kosaraju

前言

今天想起来Kosaraju，网上关于这个算法的介绍比较少。（毕竟Tarjan太强了）。但是Tarjan和Kosaraju的复杂度都是$O(V+E)$的，Kosaraju的常数要大一点。（网上有的博客说kosaraju会卡爆栈，个人感觉不会，退化成链的情况Tarjan和Kosaraju都会一搜到底）。

那为什么Kosaraju常数大还要学它呢，用Tarjan不好吗？

因为它简单、好理解啊。毕竟Tarjan难理解是出了名的。

正题

一些必要概念

网上介绍各种概念五花八门，不够深入浅出。首先要理解这几个概念：

• 前序序列（从一点开始遍历，结点进入的序列）
• 后序序列（从一点开始遍历，结点退出的序列）
• 逆后序序列（就是后序序列的逆序，没什么高深的意思，所以百度搜不到 ）
• 图$G$
• 反图$G^{\prime }$（将图$G$的各个边反过来重新建图，出边改入边）
• 强连通分量SCC（移步百度）

求前序序列和后序序列的代码（如果上面不理解，看看代码就懂了）

int n, dcnt, fcnt, c[N], d[N], vis[N], f[N];
vector<int> G[N];
void dfs(int x) {
     
    d[x] = ++dcnt;
    vis[x] = 1;
    for (auto y : G[x]) {
     
        if (!vis[y]) dfs(y);
    }
    v[x].n = ++fcnt;
}
void solve() {
     
    dcnt = fcnt = 0;
    memset(vis, 0, sizeof(vis));
    for (int i = 1; i <= n; i++) {
     
        if (!vis[i]) dfs(i);
    }
}

Kosaraju如和实现

两遍DFS：

• 第一遍，求出图G的逆后序序列。

• 第二遍，根据逆后序序列，在反图$G^{\prime }$上进行DFS，每次能dfs点就在一个强连通分量里。

代码：

int n, c[N], dfn[N], vis[N], dcnt, scnt;
vector<int> G1[N], G2[N];  // G1 原图，G2 反向图
void dfs1(int x) {
              // 求后序序列
    vis[x] = 1;
    for (auto y : G1[x]) {
     
        if (!vis[y]) dfs1(y);
    }
    dfn[++dcnt] = x;
}
void dfs2(int x) {
     
    c[x] = scnt;
    for (auto y : G2[x]) {
     
        if (!c[y]) dfs2(y);
    }
}
void kosaraju() {
     
    dcnt = scnt = 0;
    memset(c, 0, sizeof(c));
    memset(vis, 0, sizeof(vis));
    for (int i = 1; i <= n; i++) {
     
        if (!vis[i]) dfs1(i);
    }
    // 反过来遍历dfn就是逆后序序列
    for (int i = n; i >= 1; i--) {
     
        if (!c[dfn[i]]) ++scnt, dfs2(dfs[i]);
    }
}

Why？如何理解

详细的数学证明请参考《算法导论》，这里给出如何一种正确理解的方法。

首先要知道：

• 原图和反图具有相同的SCC（强连通分量）。

那为什么要求后序序列或者逆后序序列呢？

实际上是在求一个拓扑排序，但是带环图没有拓扑排序的概念，这个逆后序序列就差不多是原图缩点后的拓扑排序序列。

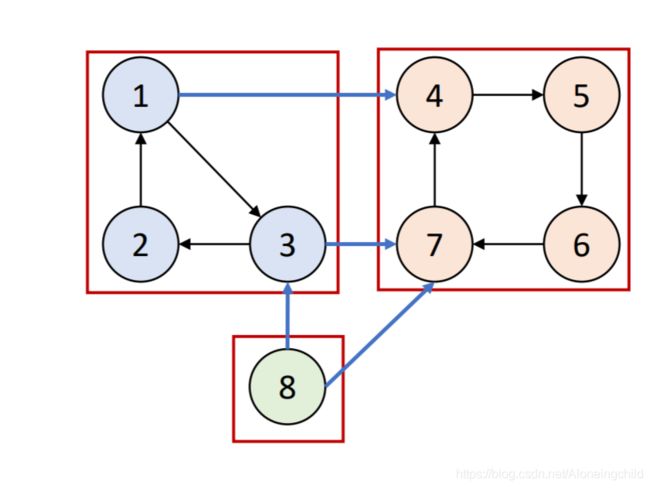
如图所示，从1号节点开始逆后序序列为：8、1、3、2、7、4、5、6

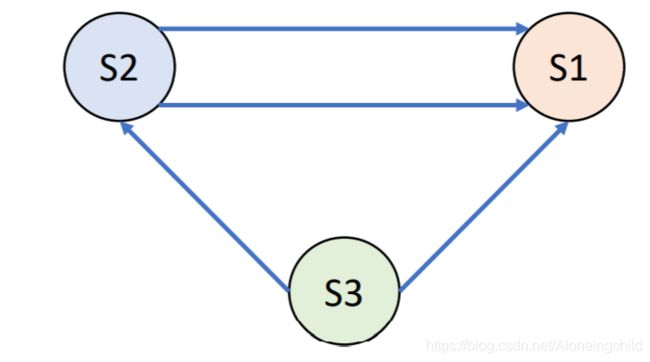
缩点后就是：

此图的拓扑排序为：S3（8）、S2（1、3、2）、S1（7、4、5、6）

然后如果在反图上按照逆拓扑序列遍历的话每次只会遍历到一个SCC。这样，这个算法就可以正常求出所有强连通分量了

问题

为什么要在反图上做逆后序序列？在原图上做后序序列不可以吗？

是这样的，上述给的例子，在原图上做后序序列是完全可以的。但只要稍加改动，原图的逆序序列有很多种（并不唯一）。比如：

• 逆后序序列1：8、1、3、2、7、4、5、6
• 逆后序序列2：8、1、3、7、4、5、6、2

序列1、2都是合法的逆序序列。上面介绍用的逆后序序列1。

他们的后序序列：

• 后序序列1：6、5、4、7、2、3、1、8

• 后序序列2：2、6、5、4、7、3、1、8

这里大家需要手动模拟一下（很简单），如果在原图上采用后序序列2，会得到错误的答案。但是在反图上采用逆后序序列2，答案仍旧正确。

因此我们只能在反图上做逆后序序列。