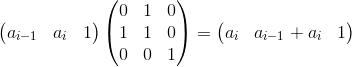bzoj 2432 [Noi2011]兔农 [矩阵]

Description

 农夫栋栋近年收入不景气，正在他发愁如何能多赚点钱时，他听到隔壁的小朋友在讨论兔子繁殖的问题。

问题是这样的：第一个月初有一对刚出生的小兔子，经过两个月长大后，这对兔子从第三个月开始，每个月初生一对小兔子。新出生的小兔子生长两个月后又能每个月生出一对小兔子。问第n个月有多少只兔子？

聪明的你可能已经发现，第n个月的兔子数正好是第n个Fibonacci(斐波那契)数。栋栋不懂什么是Fibonacci数，但他也发现了规律：第i+2个月的兔子数等于第i个月的兔子数加上第i+1个月的兔子数。前几个月的兔子数依次为：

1 1 2 3 5 8 13 21 34 …

栋栋发现越到后面兔子数增长的越快，期待养兔子一定能赚大钱，于是栋栋在第一个月初买了一对小兔子开始饲养。

每天，栋栋都要给兔子们喂食，兔子们吃食时非常特别，总是每k对兔子围成一圈，最后剩下的不足k对的围成一圈，由于兔子特别害怕孤独，从第三个月开始，如果吃食时围成某一个圈的只有一对兔子，这对兔子就会很快死掉。

我们假设死去的总是刚出生的兔子，那么每个月的兔子数仍然是可以计算的。例如，当k=7时，前几个月的兔子数依次为：

1 1 2 3 5 7 12 19 31 49 80 …

给定n，你能帮助栋栋计算第n个月他有多少对兔子么？由于答案可能非常大，你只需要告诉栋栋第n个月的兔子对数除p的余数即可。

Input

输入一行，包含三个正整数n, k, p。

Output

输出一行，包含一个整数，表示栋栋第n个月的兔子对数除p的余数。

Sample Input

6 7 100

Sample Output

7

HINT

 1<=N<=10^18
2<=K<=10^6
2<=P<=10^9

Solution

前排膜拜神题解
一道很好的矩阵乘法的题目，综合性感觉蛮强的。

以k=7为例，考虑f[i]组成的序列:
1,1,2,3,5,0,
5,5,3,0,
3,3,6,2,0,
2,2,4,6,3,2,5,0,5,5,3,0,
3,3,6,2,0,
⋯

把减1得0的位置标出，并以这些0为界分段，可以发现：

1. 每段开头必为相同两数，它恰是上一段的最末一位非0数；由于总共只有k−1种余数，所以不超过k段就会出现循环（如果有的话），比如上面k=7时的第3,4段就是循环节。

2. 记斐波那契数列为 fib[i] 。假如某段段首数字为x，那么这一段内第i个数即为 x×fib[i] 。若记这一段长度为len，则有 x×fib[len]≡1(modk) 。

现在我们试图找到整个数列的循环结构：根据上式，

① 求 x 的逆元得到 fib[len]
② 由 fib[len] 得知 len
③ 用 x×fib[len−1] 算出下一段的段首，重复操作直到发现循环（或者发现这一段永远不终止）。

至于具体实现：①扩欧或者欧拉定理②预处理indfib[y]数组，表示斐波那契数列中模k余y的数第一次出现的下标（开头的两个1不算）③预处理 fib[i] 模 k 的值。有一个结论：斐波那契数列模k后一定是0,1,1开头的纯循环，而且这个循环节的长度≤6k（不知具体怎么证。。），所以只需暴力算fib数组并同时记录 indfib[] ，发现循环即停止。
注意，假如第①步不存在逆元，或者第②步不存在符合的len，那么这一段将永远不会终止（比如k=8时就是这样），那么整个数列就不存在循环了（可以视作最后一段的长度为无穷大）。

接下来考虑如何用矩阵乘法计算f[n]。
两个重要矩乘：

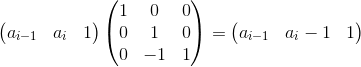
分别记这两个3×3矩阵为A,B。令初始矩阵为，通过对其不断右乘A和B便能实现累加、减1两种操作。对于分出的每一段算出一个矩阵Alen×B，表示这一段的“效果”。

接下来是喜闻乐见的分类讨论时间：假如整个数列是循环的，判断第n项是否在混循环的那部分里，若是则直接把前面几段乘起来，n所在这一段的零头直接用A的次幂算；若不是则先把混循环全部乘起来，然后把循环节全部乘起来，算出循环次数再快速幂，然后再像刚才一样算零头乘上去。若数列不循环倒方便些，也与上面类似，不多说了；如果长度无限，直接矩乘累加即可。

#include 

using namespace std;

const int MAXN = 1000005;

long long n, m, p;
long long fib[MAXN * 6], len[MAXN], vis[MAXN], ine[MAXN];
struct matrix {
    int n, m;
    long long a[3][3];
    matrix() {}
    matrix(int x, int y) {
        n = x, m = y;
        memset(a, 0, sizeof(a));
    }
};

inline matrix operator * (matrix a, matrix b) {
    if (a.m != b.n) printf("error");
    matrix c(a.n, b.m);
    for (int i = 0; i < a.n; i++)
        for (int j = 0; j < b.m; j++)
            for (int k = 0; k < a.m; k++)
                (c.a[i][j] += (a.a[i][k] * b.a[k][j]) % p) %= p;
    return c;
}

inline matrix pow(matrix a, long long x) {
    matrix res(a.n, a.m);
    for (int i = 0; i < a.n; i++)
        res.a[i][i] = 1;
    for (; x; x >>= 1, a = a * a)
        if (x & 1) res = res * a;
    return res;
}

inline long long exgcd(long long a, long long b, long long c) {
    if (a == 0) return -1;
    else if (c % a == 0) return c / a;
    long long t = exgcd(b % a, a, ((-c % a) + a) % a);
    if (t == -1) return -1;
    return (t * b + c) / a;
}

bool don[MAXN];
matrix res[MAXN];
matrix ans, mul, de;
void solve() {
    mul.n = mul.m = de.n = de.m = 3;
    bool flag = false;
    ans.n = 1, ans.m = 3;
    ans.a[0][0] = ans.a[0][2] = 1;
    mul.a[0][1] = mul.a[1][0] = mul.a[1][1] = mul.a[2][2] = 1;
    de.a[0][0] = de.a[1][1] = de.a[2][2] = 1;
    de.a[2][1] = -1;
    for (long long t = 1; n;) {
        if (!ine[t]) ine[t] = exgcd(t, m, 1);
        if (ine[t] == -1) { ans = ans*pow(mul,n); n = 0;}
        else {
            if (!don[t] || flag) {
                don[t] = 1;
                if (!vis[ine[t]]) {
                    ans = ans*pow(mul,n); n = 0;
                } else {
                    len[t] = vis[ine[t]];

                    if (n >= len[t]) {
                        n -= len[t];
                        res[t] = pow(mul, len[t]) * de;
                        ans = ans * res[t];
                        (t *= fib[len[t] - 1]) %= m;
                    } else { ans = ans*pow(mul,n); n = 0; }
                }
            } else {
                long long cnt = 0;
                matrix ret(3, 3);
                ret.a[0][0] = ret.a[1][1] = ret.a[2][2] = 1;
                for (long long i = t * fib[len[t] - 1] % m; i != t; (i *= fib[len[i] - 1]) %= m)
                    cnt += len[i], ret = ret * res[i];
                cnt += len[t], ret = res[t] * ret;
                ans = ans * pow(ret, n / cnt);
                n %= cnt;
                flag = true;
            }
        }
    }
}

int main() {
    scanf("%lld %lld %lld", &n, &m, &p);
    fib[1] = fib[2] = 1;
    for (int i = 3;; i++) {
        fib[i] = (fib[i - 1] + fib[i - 2]) % m;
        if (!vis[fib[i]]) vis[fib[i]] = i;
        if (fib[i] == 1 && fib[i - 1] == 1) break;
    }
    solve();
    printf("%lld\n", (ans.a[0][1] + p) % p);

    return 0;
}