卡方检验学习总结

 

1.卡方检验概念

1）卡方检验是一种用途很广的计数资料的假设检验方法，由卡尔·皮尔逊提出。

（1）它属于非参数检验的范畴，主要是比较两个及两个以上样本率( 构成比)以及两个分类变量的关联性分析。

（2）其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。

（3）卡方值描述两个事件的独立性或者描述实际观察值与期望值的偏离程度。卡方值越大，表名实际观察值与期望值偏离越大，也说明两个事件的相互独立性越弱。

2）在分类资料统计推断中的应用

（1）两个率或两个构成比比较的卡方检验。

（2）多个率或多个构成比比较的卡方检验以及分类资料的相关分析等。

3）可以分为成组比较（不配对资料）和个别比较（配对，或同一对象两种处理的比较）两类。

4）卡方检验是非参数检验的一种，其稳健性不及参数检验，因此，从使用的角度来看，应首选参数检验，如果在无法满足参数检验基础条件的前提下，再考虑非参数检验。

（1）参数检验对观测值的普遍要求是总体呈现正态分布，但实际研究中，不是所有观测值都呈现正态分布，或者无法确定其是否正态分布。由于缺乏足够的信息，总体分布未知，这些情况下，参数检验技术就未必适用了。

（2）最常用的非参数检验技术就是卡方检验，它最适合于次数分布检验。

5）卡方检验的应用主要

（1）卡方拟合优度检验

拟合优度检验是用卡方统计量进行统计显著性检验的重要内容之一。它是依据总体分布状况，计算出分类变量中各类别的期望频数，与分布的观察频数进行对比，判断期望频数与观察频数是否有显著差异，从而达到从分类变量进行分析的目的。

（2）卡方独立性检验

独立性检验是统计学的一种检验方式，与适合性检验同属于X2检验，即卡方检验（英文名：chi square test），它是根据次数资料判断两类因子彼此相关或相互独立的假设检验。

6）卡方检验公式

（1）CHI值用于衡量实际值与理论值的差异程度，除以T是为了避免不同观察值与不同期望之间产生的偏差因T的不同而差别太大，所以除以E以消除这种弊端。

• 实际值与理论值偏差的绝对大小（由于平方的存在，差异被放大）
• 差异值与理论值的相对大小

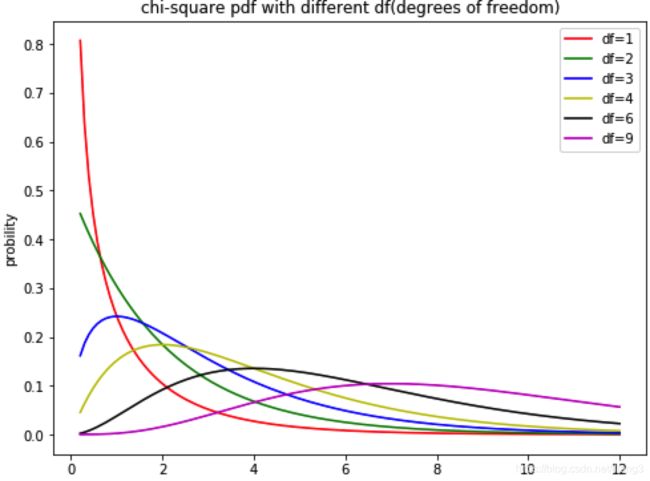
（2）不同自由度的卡方分布概率密度函数

由于卡方越大表示差异越大，此时的p值计算的是观测分布和期望分布的差异大于卡方值的概率

（3）自由度计算：(行数-1)*(列数-1)

自由度计算例子

         

          图片中的自由度=(2-1)*(2-1)=1

（3）随着CHI的增大，原假设成立的概率就越小。

         

7）卡方检验流程

（1）列出相关性表

• 相关性表的每列是每一种目标值，如患病和不患病、有效和无效、骰子取值123456等。
• 相关性表的每一行是每种条件，如吸烟和不吸烟、喝牛奶和不喝牛奶、观察值和期望值等。

（2）定义假设问题

• 原假设H0：假设纵列因素不影响横行的因素的变化
• 备择假设H1：纵列因素对横行的因素变化有影响

（3）计算CHI值

（4）计算相关性表的理论值

（5）计算自由度

（6）设定置信度/显著性值，一般选择0.9、0.95、0.99、0.995、0.999等

假如选择显著性水平=0.05，则H0成立的可能性（置信度）小于0.5%，即H1的概率大于99.5%。

（7）通过卡方分布的临界值表判断假设是否成立

• 计算出的CHI值表示实际值与理论值的差异，越大表示实际值与理论值不符，即越有可能纵列因素会影响横行数值，列因素不影响横行值的范围：0~临界值。
• 如果计算出的CHI值大于临界值，我们就排斥原假设，接受备择假设；反之，卡方值小于临界值，即在理论范围内，无法推翻原假设，即无统计差异，接受原假设。

2. 卡方检验例子

1）例子：检验喝牛奶对感冒有没有影响

（1）喝牛奶与感冒的相关性

（2）计算理论值

如果喝牛奶对感冒没有影响，那么喝不喝牛奶的感冒率都应该一样，所以使用人群总的感冒率来计算喝牛奶组以及不喝牛奶组的感冒人数。

         

（3）计算CHI值

CHI=(43-39.3231)^2/39.3231+(28-31.6848)^2/31.6848+(96-99.6769)^2/99.6769+(84-80.3152)^2/80.3152=1.077

（4）计算自由度V=(2-1)*(2-1)=1

（5）通过卡方分布的临界值表判断喝牛奶和感冒是否真的独立无关。

• 第一行表示显著性水平，第一列表示自由度。
• 喝牛奶和感冒（95%概率）不相关的卡方分布的临界值（最大临界值）是3.84，即如果CHI大于3.84，则认为喝牛奶和感冒（有95%的概率）有关。显然1.077<3.84，没有达到卡方分布的临界值，所以喝牛奶和感冒独立不相关的假设成立。
• 说明：临界值3.84的意义表示：如果卡方值>3.84，则纵列因素和横行因素不相关的概率<0.05（即显著性水平），也即纵列因素和横行因素相关的概率>0.95。

2）例子：不吃晚饭对体重下降没有影响

（1）相关性数据

（2）建立假设检验

• H0：r1=r2，不吃晚饭对体重下降没有影响，即吃不吃晚饭的体重下降率相等。
• H1：r1≠r2，不吃晚饭对体重下降有显著影响，即吃不吃晚饭的体重下降率不相等。

（3）计算理论值

590*0.2267=133.765

590*(1-0.2267)=456.234

151*0.2267=34.2348

151*(1-0.2267)=116.765

（4）计算CHI值：(123-133.765)^2/133.765 + (467-456.234)^2/456.234 + (45-34.2348)^2/34.2348 + (106-116.765)^2/116.765=5.498

（5）计算自由度：(2-1)*(2-1)=1

（6）选择显著性水平=0.05，H0成立的可能性（置信度）小于0.5%，即H1的概率大于99.5%。

（7）通过卡方分布的临界值表判断假设是否成立

• 查表得到3.84，而CHI值>3.84，差异有显著统计学意义，按显著性水平0.05水准，拒绝H0，可以认为两组的体重下降率有明显差别。
• 所以不吃晚饭对体重下降有影响。

3）例子：根据投硬币的结果，判断硬币是否均衡

（1）相关性表数据

（2）建立假设检验

• H0：硬币是均衡的（理论值与观测值差异不大）
• H1：硬币是不均衡的

（3）卡方值：(28-25)^2/25 + (22-25)^2/25 = 0.72

（4）自由度：(2-1)*(2-1)=1

（5）置信度选择95%

（6）0.72小于查表得到3.841， 所以有95%的把握说这个硬币是均衡的。

4）例子：电商中消费者的性别对购买生鲜是否有影响

（1）相关性数据

（2）建立假设检验

• H0：性别对是否购买生鲜不影响
• H1：性别对是否购买生鲜有影响

（3）计算理论值

（4）计算卡方值：(206-249)^2/249 + (102-59)^2/59 + (527-484)^2/484 + (72-115)^2/115=58.4

（5）自由度：(2-1)*(2-1)=1

（6）选择置信度90%

（7）58.4大于查表值2.71，拒绝H0，接受H1假设。所以不同的性别和在线上购买生鲜食品是有关系的。

3. 使用卡方检验进行特征筛选

1）CHI值越大，说明两个变量越不可能是独立无关的，也就是说CHI值越大，两个变量的相关程度也越高。

（1）对于特征变量x1,x2,…,xn，以及分类变量y。只需要计算CHI(x1,y)、CHI(x2,y)、…、CHI(xn,y)，并按照CHI的值从大到小将特征排序。

（2）然后选择阈值，大于阈值的特征留下，小于阈值的特征删除。这样筛选出一组特征子集就是输入模型训练的特征。 。

2）程序实现

（1）sklearn.feature_selection.SelectKBest：返回k个最佳特征

（2）sklearn.feature_selection.SelectPercentile：返回表现最佳的前r%个特征

（3）例子：使用卡方检验选择特征

    #导入sklearn库中的SelectKBest和chi2

    from sklearn.feature_selection import SelectKBest ,chi2

    #选择相关性最高的前5个特征

    X_chi2 = SelectKBest(chi2, k=5).fit_transform(X, y)

    X_chi2.shape

    输出：(27, 5)

（4）其它可选的方法

• f_classif: ANOVA F-value between label/feature for classification tasks.
• mutual_info_classif: Mutual information for a discrete target.
• chi2: Chi-squared stats of non-negative features for classification tasks.
• f_regression: F-value between label/feature for regression tasks.
• mutual_info_regression: Mutual information for a continuous target.
• SelectPercentile: Select features based on percentile of the highest scores.
• SelectFpr: Select features based on a false positive rate test.
• SelectFdr: Select features based on an estimated false discovery rate.
• SelectFwe: Select features based on family-wise error rate.
• GenericUnivariateSelect: Univariate feature selector with configurable mode.

 

参考文献 

[1]. 使用R语言进行卡方检验（chi-square test）. https://www.jianshu.com/p/bb0bd72bc428

[2]. 结合日常生活的例子，了解什么是卡方检验. https://www.jianshu.com/p/807b2c2bfd9b