神秘国度的爱情故事--数据结构课程设计
结论:最开始N个结点的树,处理M组数据,采用深度优先搜索,总时间复杂度为O(NM)。优化方法是找最近公共祖先(lca)的倍增法。N个结点的树,每次找最近公共祖先的时间复杂度为O(logN),处理M组数据,总时间复杂度为O(MlogN)。
一、实验目的
- 理解问题的要求并设计出合理的方法来解决。
- 选择适合的数据结构处理问题。
- 设计算法解决问题。
- 通过比较算法的时间复杂度和空间复杂度来选择更优的算法。
二、使用仪器、器材
微机一台
操作系统:Win10
编程软件:Visual Studi0 2015 C++
三、实验内容及原理
实验内容:
某个太空神秘国度中有很多美丽的小村,从太空中可以想见,小村间有路相连,更精确一点说,任意两村之间有且仅有一条路径。小村 A 中有位年轻人爱上了自己村里的美丽姑娘。每天早晨,姑娘都会去小村 B 里的面包房工作,傍晚 6 点回到家。年轻人终于决定要向姑娘表白,他打算在小村 C 等着姑娘路过的时候把爱慕说出来。问题是,他不能确定小村 C 是否在小村 B 到小村 A 之间的路径上。你可以帮他解决这个问题吗?
输入要求:输入由若干组测试数据组成。每组数据的第 1 行包含一正整数 N ( l 《 N 《 50000 ) , 代表神秘国度中小村的个数,每个小村即从0到 N - l 编号。接下来有 N -1 行输入,每行包含一条双向道路的两个端点小村的编号,中间用空格分开。之后一行包含一正整数 M ( l 《 M 《 500000 ) ,代表着该组测试问题的个数。接下来 M 行,每行给出 A 、 B 、 C 三个小村的编号,中间用空格分开。当 N 为 O 时,表示全部测试结束,不要对该数据做任何处理。
输出要求:对每一组测试给定的 A 、 B 、C,在一行里输出答案,即:如果 C 在 A 和 B 之间的路径上,输出 Yes ,否则输出 No.
算法设计思路:
1、在拿到题目后,当看到“任意两村之间有且仅有一条路径”,可以知道这些(小村)结点是没有回路的,也就是构成一颗树的形状,所以首先想到的是用树的方法处理这道题。
2、在接下来阅读题目,发现是要找C是否在AB之间,首先想到采用从A遍历到B的过程中判断是否经过C点。但是在树的遍历有先序、中序和后序,都不适用于路径的查找。同时,和一个(小村)结点相连的结点可能不止两个,用学过的二叉树存储肯定不行。所以采用了图的方式来处理这颗树,存储方式是邻接表,遍历方式采用了深度优先搜索。
3、如果采用深度优先搜索,最坏的情况是每个结点都要遍历一次,所以它的时间复杂度是O(N),N是结点的个数。另外每一组测试数据都要处理,时间复杂度是O(M),M是测试数据的个数。每一组测试数据都要深度优先搜索遍历一遍,所以总的时间复杂度是O(NM),当N、M很大时,这是相当耗费时间的,要优化算法。
4、第一个优化是在创好邻接表后,先以0为根结点深度优先遍历一次,把每个结点的深度和父结点找到并存储起来。处理一组数据时,只要知道A和B的深度并都往上遍历到根结点,在这个过程中判断是否经过C点就行。但有一种情况,就是A和B往上走时很快在某个祖先结点相遇,所以在接下来走到根结点的过程中可能会出错、误判,或者因为重复而导致时间耗费。所以继续优化,采用找最近公共祖先。
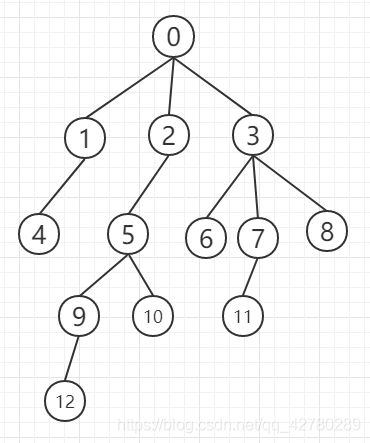
5、最近公共祖先,顾名思义,就是两个结点的共同的祖先,同时也是距离两个结点最近的。如下图中9、11的最近公共祖先是0,12、10的最近公共祖先是5。思路是先让AB中深度大的结点先往上走到和深度小的结点同深度,然后两个结点同时往上走并判断是否相等,相等即找到最近公共祖先,在这个过程中要判断是否经过C。
但是,当这棵树是一颗单链的树,这些优化并不起很好作用,时间复杂度还是O(NM)。通过查找资料,最后采用了处理最近公共祖先的算法之一-----倍增法。
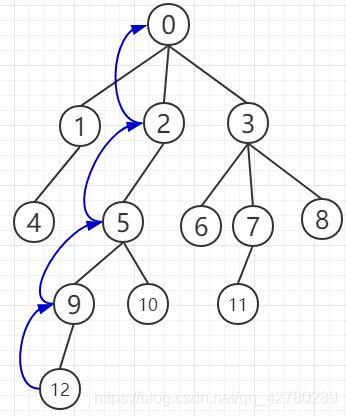
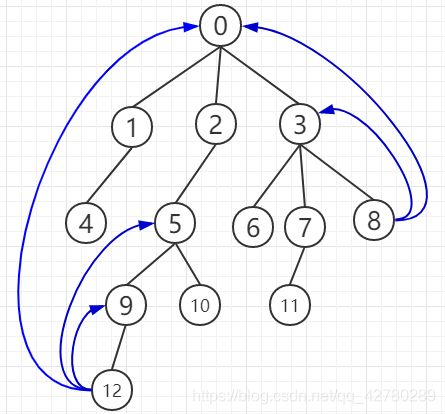
6、找公共祖先所用的倍增法基本原理其实就是往上走的时候不是采用一步步走(如图1),而是采用往上跳2的倍数的方法。比如(图2)中,12可以往上跳1步到9,可以往上跳2步到5,也可以往上跳4步到根结点0。要使用倍增法,必须先预处理一个用来倍增的数组,里面存储了每个结点往上倍增的信息,预处理的时间复杂度是O(NlogN),N是结点个数。
图1 图2
预处理我用grand[50000][30]数组来存储,第一个是结点的编号;第二个是倍增的距离,是2的次方,比如grand[30][3]表示结点30往上跳2^3=8距离的结点编号。因为之前第一次处理时获取了每个结点的深度和父结点,grand[xx][0]是往上跳1步,也就是父结点。下面演示预处理的一部分(用上面的图2,从根结点0出发,深度搜索):
往上跳1步,等于父结点:grand[v][0] = nodelist[v].pre;
往上跳2^i步:grand[v][i] = grand[ grand[v][i - 1] ] [i - 1]; -----重点理解,自己试一遍
结点0:grand[0][0],根结点的父结点不存在。
结点2:grand[2][0]=0。
结点5:grand[5][0]=2; grand[5][1]=grand[grand[5][0]] [0]=grand[2][0]=0。
结点9:grand[9][0]=5; grand[9][1]=grand[grand[9][0]] [0]=grand[5][0]=2。
结点12:grand[12][0]=9; grand[12][1]=grand[grand[12][0]] [0]=grand[9][0]=5。
grand[12][2]=grand[grand[12][1]] [1]=grand[5][1]=0。
以此类推。
7、预处理好后,就可以用来找最近公共祖先。思路和步骤5类似,先让深度大的跳到和深度小的同深度,然后两个结点同时往上跳,只不过每次往上跳都采用倍增法,也就是预处理好的grand数组。因为用倍增法可能会跳过C,所以我才采用的方法是分别计算出A和B,A和C以及B和C的最近公共祖先,再判断C是否在AB之间。
四、实验过程原始数据记录
代码:
#include
using namespace std;
#define MVnum 50010
#define Testnum 500000
typedef struct VNode
{
int data; //结点的数据(小村的编号)
VNode *next;
int depth; //结点所在树的深度信息
int pre; //父结点的编号
}VNode;
typedef struct Testdata
{
int lval, rval, fval; //测试数据的左右数值(A、B)和查找的数值(C)
}Testdata;
int N, M; //N是结点(小村)的个数,M是测试问题的个数
VNode nodelist[MVnum]; //顶点表
Testdata testdata[Testnum]; //存储测试数据
/*-------------------------输入结点并创建邻接表---------------------------------*/
void create_udg()
{
cout << "请输入结点个数:" << endl;
cin >> N;
for (int i = 0; i < N - 1; i++)
{
nodelist[i].data = i;
nodelist[i].next = NULL; //初始化顶点
}
cout << "请输入" << N - 1 << "组相邻的两个结点:" << endl;
int x, y; //两个结点(小村)的编号
for (int i = 0; i < N - 1; i++)
{
cin >> x >> y;
//x连接y
VNode *p1 = new VNode;
p1->data = y;
p1->next = nodelist[x].next;
nodelist[x].next = p1;
//y连接x
VNode *p2 = new VNode;
p2->data = x;
p2->next = nodelist[y].next;
nodelist[y].next = p2;
}
}
/*-------------------------输入测试数据---------------------------------*/
void input_test()
{
cout << "请输入测试数据组数:" << endl;
int l, r, f;
cin >> M;
cout << "请输入" << M << "组测试数据:" << endl;
for (int i = 0; i < M; i++) //用结构体存储测试数据
{
cin >> r >> l >> f;
testdata[i].rval = r;
testdata[i].lval = l;
testdata[i].fval = f;
}
}
/*-------------------------第一次深度优先搜索遍历--------------------------------*/
//统计信息,用于设置结点的深度,父结点的编号
int visited[MVnum]; //标志数组,初值为0
void dfs_f(int pre, int v, int depth) //pre是父结点,v是顶点,d是深度
{
// cout << v << endl;
visited[v] = 1;
nodelist[v].depth = depth;
nodelist[v].pre = pre;
VNode *p = nodelist[v].next;
while (p != NULL)
{
int w = p->data;
if (!visited[w]) dfs_f(v, w, depth + 1);
p = p->next;
}
}
/*---------------------------第二次深度优先搜索遍历--------------------------------*/
//预处理找最近公共祖先的数组(倍增法)
int grand[40001][20]; //第一个是结点,第二个是倍增的x,即2^x(2的x次方)
//最多能跳2^d个祖先
int find_jump(int depth)
{
int high = 0;
for (int d = 0; d < 30; d++)
{
high = pow(2, d);
if (high > depth) return d - 1;
}
}
//第二次深度优先搜索遍历,预处理找最近公共祖先的数组grand(倍增法),时间复杂度为(O(nlogn))
int visited_2[MVnum];
void dfs_s(int v)
{
visited_2[v] = 1;
int depth = nodelist[v].depth;
int n = find_jump(depth); //找到最大但不超过根结点的2的次方数
for (int i = 0; i <= n; i++)
{
if (i == 0) {
grand[v][0] = nodelist[v].pre; //父结点,直接用之前遍历出来的
}
else {
grand[v][i] = grand[grand[v][i - 1]][i - 1]; //倍增法,不断借用之前处理出来的
}
}
VNode *p = nodelist[v].next;
while (p != NULL)
{
int w = p->data;
if (!visited_2[w]) dfs_s(w);
p = p->next;
}
}
/*-----------------------找最近公共祖先--------------------------------*/
//lac算法(用的是倍增法)找最近公共祖先
int lca(int l, int r) //l是左结点编号,r是右结点编号
{
if (nodelist[l].depth > nodelist[r].depth) { //保持l在r的上面,便于计算
int temp = l;
l = r;
r = temp;
}
/* 结果:l是深度小的,r是深度大的 */
int ldepth = nodelist[l].depth;
int rdepth = nodelist[r].depth;
int rn = find_jump(rdepth);
for (int i = rn; i >= 0; i--) //把在下面的r跳到和l同深度
{
if (ldepth < nodelist[r].depth && nodelist[grand[r][i]].depth >= ldepth) {
r = grand[r][i];
}
}
//同层次后,两个结点一起往上跳
int ln = find_jump(ldepth);
for (int i = ln; i >= 0; i--)
{
if (grand[l][i] != grand[r][i]) { //可能会跳到最近公共祖先结点上面,相等但不满足
l = grand[l][i];
r = grand[r][i];
}
}
int ans = l; //情况出现在,最开始的l和r在同一支路上,通过上面跳到同一深度就直接找到
if (l != r) { //l不等于r,公共祖先就在上一深度
ans = grand[l][0];
}
return ans;
}
//主函数
int main()
{
create_udg(); //输入结点并创建邻接表
input_test(); //输入测试数据
//第一次深度遍历,第二个参数是遍历的根结点,第一个参数-1是根结点的父结点,不存在置为-1;
//第三个参数是深度
dfs_f(-1, 0, 0);
//第二次深度遍历,参数是根结点0,用于预处理倍增法要用的数组grand[]
dfs_s(0);
int a, b, c; //测试的三个数据
int lca_ab, lca_ac, lca_bc; //三个数据两两之间的最近祖先结点
char *results[Testnum]; //存储最后的结果,yes或者no
for (int i = 0; i < M; i++) //遍历所有测试数据(时间复杂度:O(M))
{
a = testdata[i].lval;
b = testdata[i].rval;
c = testdata[i].fval;
lca_ab = lca(a, b); //找最近公共祖先,时间复杂度(O(logn))
lca_ac = lca(a, c);
lca_bc = lca(b, c);
if ((lca_ab == c) || ((lca_ac == c) && (lca_bc != c)) ||
((lca_ac != c) && (lca_bc == c))) {
results[i] = "yes";
}
else {
results[i] = "no";
}
}
//输出结果
cout << "结果:" << endl;
for (int i = 0; i < M; i++)
{
cout << results[i] << endl;
}
return 0;
}
操作结果:
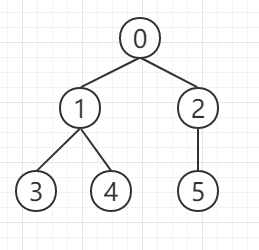
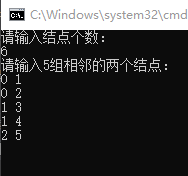
1、测试数据采用的是如下图所示的树,共6个结点。
在上图的树中,分析结果是否正确。当A=3,B=2,C=0时结果输出yes,在图中0确实在3和2的路径中间。当A=3,B=2,C=5时结果输出no,在图中5确实不在3和2的路径中间。所以测试数据都是正确的。
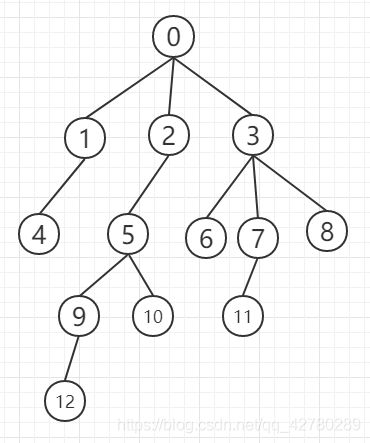
2、测试数据采用的是如下图所示的树,共13个结点。
下面开始测试,先输入N=13个结点,再依次输入树中两两相邻的边,接着输入M=4个测试数据,然后依次输入测试数据A、B、C,最后输出测试结果。
在上图的树中,分析结果是否正确。当A=1,B=3,C=0时结果输出yes,在图中0确实在1和3的路径中间。当A=12,B=6,C=2时结果输出yes,在图中2确实在12和6的路径中间。当A=12,B=6,C=7时结果输出no,在图中7确实不在12和6的路径中间。当A=4,B=5,C=8时结果输出no,在图中8确实不在4和5的路径中间。所以测试数据都是正确的。
五、实验结果及分析
实验结果:
1、测试数据,50000个结点和50000组测试数据,形成单链树的形式。
测试结果:
测试时间=总时间-读取文件时间;1.527s-0.916s=0.611s
因为总时间大部分是从文件读取数据的时间,所以要从总时间中减去文件读取数据的时间,才是处理数据的时间,可以看到结果,50000个结点形成的单链树,测试50000组数据的时间为0.611s。
2、测试最大数据,50000个结点和500000组测试数据,形成单链树的形式。
测试结果:
测试时间=总时间-读取文件时间;8.32s-5.535s=2.785s
因为总时间大部分是从文件读取数据的时间,所以要从总时间中减去文件读取数据的时间,才是处理数据的时间,可以看到结果,50000个结点形成的单链树,测试500000组数据的时间为2.785s。
实验分析:
- 在最开始处理这道题的时候,并没有想到好的算法来实现,所以采用的是用图的邻接表来存储这棵树的结点,然后在处理每组测试数据时都深度优先搜索遍历一次来查找C是否在A、B之间。所以时间复杂度很高,M组测试数据,每组测试数据最坏情况遍历全部结点N个,即M*N,时间复杂度为O(NM)。在测试大数据时,这个复杂度的算法处理效果很不理想。
- 接着采用了一些小方法来优化,一个是给每个结点加上深度,处理AB路径时只需往深度小的方向,也就是根结点方向走,所以并不需要遍历路径之外的结点,可以节省一些时间。然后考虑到两个结点往上走的路径重合后会重复遍历相同结点,另外也不需要遍历重复结点,所以采用了找最近公共祖先的方法。但是,考虑到极端情况下树变成了单链的形式,这两种优化方法都不能彻底解决问题,还是要一步步遍历,时间复杂度是O(N),N是结点个数,总时间复杂度就还是O(NM)。
- 最后采用的是结合上面的两个方法和倍增法来处理。倍增法是采用每次跳2的倍数来实现优化,在这之前要先预处理好用来倍增的数组,预处理的时间复杂度是O(NlogN)。处理好后在处理测试数据时,要找三个结点两两之间的最近公共祖先,每找一次最近公共祖先的时间复杂度是O(logN),三次即O(3logN)。另外有M组测试数据,所以最后的时间复杂度是O(3MlogN),也可以看做O(MlogN)。用来处理50000个结点和500000组数据大小效率基本没问题。