左偏树——杨子曰数据结构

左偏树——杨子曰数据结构

先扔出一道题（【洛谷】P3377 【模板】左偏树（可并堆））：

题目描述
如题，一开始有N个小根堆，每个堆包含且仅包含一个数。接下来需要支持两种操作：

操作1： 1 x y 将第x个数和第y个数所在的小根堆合并（若第x或第y个数已经被删除或第x和第y个数在用一个堆内，则无视此操作）

操作2： 2 x 输出第x个数所在的堆最小数，并将其删除（若第x个数已经被删除，则输出-1并无视删除操作）

输入格式
第一行包含两个正整数N、M，分别表示一开始小根堆的个数和接下来操作的个数。

第二行包含N个正整数，其中第i个正整数表示第i个小根堆初始时包含且仅包含的数。

接下来M行每行2个或3个正整数，表示一条操作，格式如下：

操作1 ： 1 x y

操作2 ： 2 x

输出格式
输出包含若干行整数，分别依次对应每一个操作2所得的结果。

输入输出样例

输入

5 5
1 5 4 2 3
1 1 5
1 2 5
2 2
1 4 2
2 2

输出

1
2

说明/提示
当堆里有多个最小值时，优先删除原序列的靠前的，否则会影响后续操作1导致WA。

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=1000，M<=1000

对于100%的数据：N<=100000，M<=100000

样例说明：

初始状态下，五个小根堆分别为:{1}、{5}、{4}、{2}、{3}。

第一次操作，将第1个数所在的小根堆与第5个数所在的小根堆合并，故变为四个小根堆：{1,3}、{5}、{4}、{2}。

第二次操作，将第2个数所在的小根堆与第5个数所在的小根堆合并，故变为三个小根堆：{1,3,5}、{4}、{2}。

第三次操作，将第2个数所在的小根堆的最小值输出并删除，故输出1，第一个数被删除，三个小根堆为：{3,5}、{4}、{2}。

第四次操作，将第4个数所在的小根堆与第2个数所在的小根堆合并，故变为两个小根堆：{2,3,5}、{4}。

第五次操作，将第2个数所在的小根堆的最小值输出并删除，故输出2，第四个数被删除，两个小根堆为：{3,5}、{4}。

故输出依次为1、2。

---

说白了就是让你维护好几个堆，可以求最值，弹出，合并

让我们用一个nb的数据结构——左偏树，来解决这道题

---

首先，左偏树长这样：

哦，不好意思o(￣┰￣*)ゞ，放错图了，是这张：

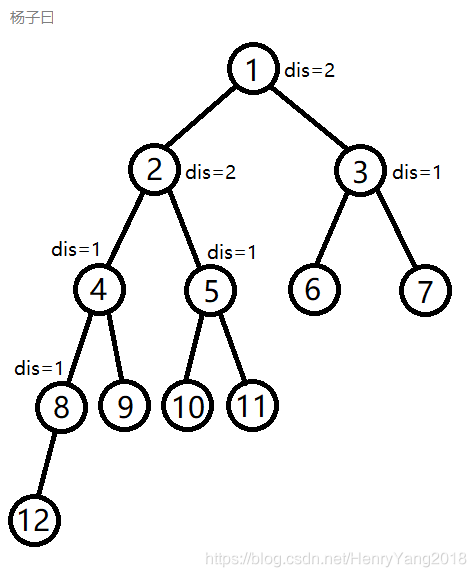
这棵树明显地向左偏了呀！这就是为什马它叫左偏树

先来说一下对于这棵树上的每个结点我们要记录什么：

• ls：左儿子
• rs：右儿子
• v：权值
• f：用来维护并查集的东西，用它来找到当前结点的根
• dis：左偏树中最最重要的东西，就是从当前结点出发，不停往右儿子走，能走多远

我们把dis标上来给大家瞅瞅（没有标的dis是0）：

然后我们来曰一曰左偏树需要满足的性质：

• 满足小根堆或者大根堆的性质
• 对于每个节点$dis[ls]\ge dis[rs]$，这也就是它左偏的性质

那么我们怎么来维护这个dis捏？特别简单，对于结点i的dis：dis[i]=dis[rs[i]]+1，特别好理解！

在开始讲各种操作之前，我们先要说明一个事情，根结点的dis不会超过log n，也就是整棵树最右边那条链的长度不会超过log n：
我们假设最右边那条链上的结点个数为x，我们手动模一下会发现：为了维护每个dis，点最少最少也需要大致上构成一个满二叉树So，最右边那条链一定是log级别的，这也就是它复杂度如此优秀的原因

---

好的，接下来我们讲一讲怎么解决上面的那道题目：

首先，我们要用一个并查集来维护每个结点所在左偏树的根的编号，每个结点记录的f值就是用来做并查集的，这我就不多讲了

1. 合并（merge）
   
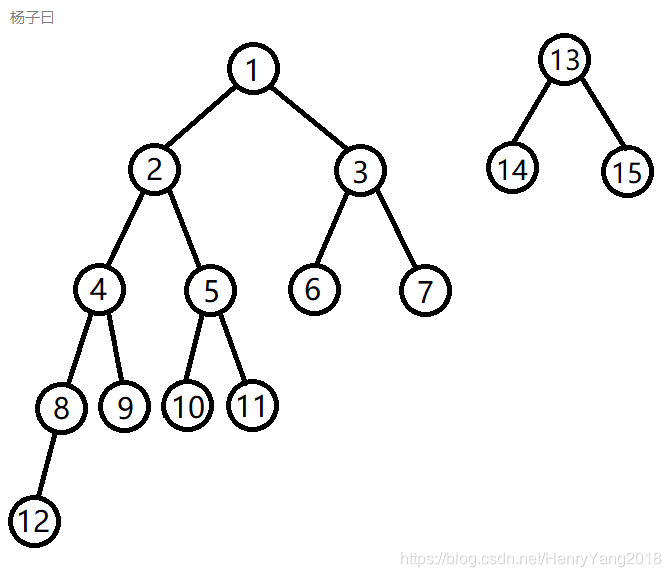
   我们需要维护堆的性质，So，我们就比较一下我们要合并的两棵树的根的权值由于是小根堆，那我们就要让权值小的点成为新的根，然后合并新的根的右儿子和另一棵树。比如上面那个图，经过一番比较以后发现v[1]
   然后就变成了一个新的子问题，不断递归下去，直到两颗子树右一颗子树空了。
   当然，这样合并完以后整条路径上的dis可能都不准了，So，我们要在回溯的时候把dis数组更新一下。
   “那如果惊悚的发现某个结点左儿子的dis小于了右儿子的dis，也就是不满足左偏树的性质了怎么办？”
   “不要紧张，直接更换它的左右儿子！”
   完事。

int merge(int l,int r){
	if (l==0 || r==0) return l+r;
	if (t[l].v>t[r].v || (t[l].v==t[r].v && l>r)) swap(l,r);
	t[l].rs=merge(t[l].rs,r);
	if (t[t[l].ls].dis<t[t[l].rs].dis) swap(t[l].ls,t[l].rs);
	t[t[l].ls].f=t[t[l].rs].f=t[l].f=l;
	t[l].dis=t[t[l].rs].dis+1;
	return l;
}

2. 弹出/删除（del）
   这个操作实在是太简单了，我们要弹出这颗左偏树的根，我们只要完全忽视根节点，把它的两棵子树合并,完事。
   （不过要注意一点，假设我们要删掉x，由于原来x的有些后代的f数组指向了x，而x被删掉后他们应该指向的是x的两个儿子合并后新的根，那我们这样来处理：虽然x被删了，我们把x的f值附成两个儿子合并后新的根，这样它的后代在并查集中找根的时候就可以找到正确的根了）
   

void del(int x){
	t[x].v=-1;
	t[t[x].ls].f=t[x].ls;
	t[t[x].rs].f=t[x].rs;
	t[x].f=merge(t[x].ls,t[x].rs);
}

3. 查询最值（query）
   这个就更简单了，我们用维护的并查集找到这棵树的根，输出根上的权值，完事。

int query(int x){
	int fx=gf(x);
	return t[fx].v;
}

由于在合并的时候我们只会往右儿子走，而我们又说明最右边那条链的长度是log级别的，自然它的时间复杂度也是O(log n)的。

OK，完事

---

c++代码（洛谷 P3377）：

#include
using namespace std;

const int maxn=150005;

struct Tr{
	int ls,rs,dis,v,f;
}t[maxn];

int n,m;

int gf(int x){
	return t[x].f==x?x:t[x].f=gf(t[x].f);
}

int merge(int l,int r){
	if (l==0 || r==0) return l+r;
	if (t[l].v>t[r].v || (t[l].v==t[r].v && l>r)) swap(l,r);
	t[l].rs=merge(t[l].rs,r);
	if (t[t[l].ls].v==-1 || t[t[l].ls].dis<t[t[l].rs].dis) swap(t[l].ls,t[l].rs);
	t[t[l].ls].f=t[t[l].rs].f=t[l].f=l;
	t[l].dis=t[t[l].rs].dis+1;
	return l;
}

void del(int x){
	t[x].v=-1;
	t[t[x].ls].f=t[x].ls;
	t[t[x].rs].f=t[x].rs;
	t[x].f=merge(t[x].ls,t[x].rs);
}

int query(int x){
	int fx=gf(x);
	return t[fx].v;
}

int main(){
	scanf("%d%d",&n,&m);
	for (int i=1;i<=n;i++){
		scanf("%d",&t[i].v);
		t[i].f=i;
	}
	while(m--){
		int opt;
		scanf("%d",&opt);
		if (opt==1){
			int x,y;
			scanf("%d%d",&x,&y);
			int fx=gf(x),fy=gf(y);
			if (t[x].v==-1 || t[y].v==-1) continue;
			if (fx==fy) continue;
			t[fx].f=t[fy].f=merge(fx,fy);
		}
		else{
			int x;
			scanf("%d",&x);
			if (t[x].v==-1){
				puts("-1");
				continue;
			}
			printf("%d\n",query(x));
			del(gf(x));
		}
	}
	return 0;
}

于HG机房