数据结构学习（九）：线段树（SegmentTree）

一、概念介绍

1.概念：

线段树是一种高级的数据结构，常用来处理区间范围问题，如：

①区间查询：如给定一个数组int [ ]arr={-1,-2,0,1,2,3,-3,0},需要反复查询[i,j]范围内的和（也可以是自定义的某种融合方法，加减乘除等等）

②墙壁涂色：给定一面墙壁，假设1代表红色，2代表黄寺，3代表蓝色，【1,2,3,3,3,2,1】

需要反复查询[i,j]范围内总共有多少种颜色。甚至会对墙壁进行涂色覆盖，再求范围内的不同颜色的总数。

2.结构

①线段树的结构类似于二叉树

根节点存储[i,j]所有元素的和（假设融合方法是求和）

左孩子存储[i,mid]所有元素的和（mid=l+(r-l)/2）

右孩子存储[mid+1,j]所有元素的和

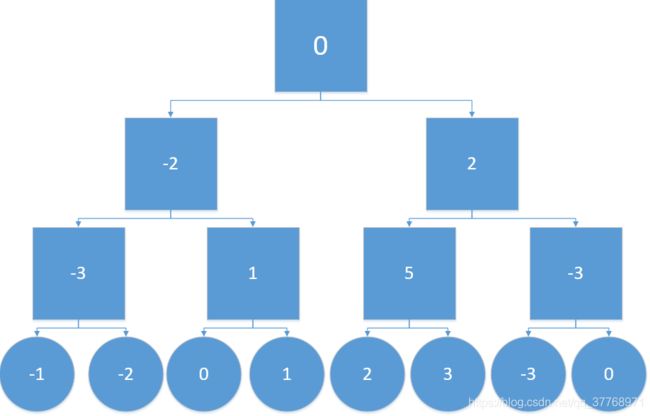
int [ ]arr={-1,-2,0,1,2,3,-3,0}生成的线段树如下：

3.为了方便使用，线段树采用数组的方式进行存储
其中左孩子和右孩子的计算方法如下：

public int leftChild(int index){
    return index*2+1;
}
public int rightChild(int index){
    return index*2+2;
}

二、代码和注释

//融合器，用于用于自定义融合的方法（如：相加）
public interface Merger {
    public E merge(E left,E right);
}

 

public class SegmentTree {
   private E data[];
   private E tree[];
   private Mergermerger;
   public SegmentTree(E []arr,Mergermerger){
       data=(E[])new Object[arr.length];
       tree=(E[])new Object[4*arr.length];//最坏的情况下，线段树的大小需要比原来数组的大小大四倍
       this.merger=merger;
       for (int i=0;i=data.length)throw new IllegalArgumentException("Index is illegal!");
       return data[index];
   }

   public int getSize(){
       return data.length;
   }

   public int leftChild(int index){
       if (index<0||index>+data.length)throw new IllegalArgumentException("Index is illegal!");
       return index*2+1;
   }
   public int rightChild(int index){
       if (index<0||index>+data.length)throw new IllegalArgumentException("Index is illegal!");
       return index*2+2;
   }
    //用于创建线段树
   public void buildSegmentTree(int treeIndex,int l,int r){
       if (l==r){
           tree[treeIndex]=data[l];
           return;
       }
       int mid=l+(r-l)/2;
       int treeLeftChild=leftChild(treeIndex);
       int treeRightChild=rightChild(treeIndex);
       buildSegmentTree(treeLeftChild,l,mid);
       buildSegmentTree(treeRightChild,mid+1,r);
       tree[treeIndex]=merger.merge(tree[treeLeftChild],tree[treeRightChild]);
   }

    //用于查询[queryL,queryR]之间的和
    public E query(int queryL,int queryR){
       if (queryL<0||queryL>=data.length||queryR<0||queryR>=data.length||queryL>queryR)
           throw new IllegalArgumentException("Index is illegal!");
        return query(0,0,data.length-1,queryL,queryR);
    }

    private E query(int treeIndex,int l,int r,int queryL,int queryR){
       int mid =l+(r-l)/2;
       int treeLeftChild=leftChild(treeIndex);
       int treeRightChild=rightChild(treeIndex);
        if (l==queryL&&r==queryR){
            return tree[treeIndex];
        }
        if (queryL>mid){
            return query(treeRightChild,mid+1,r,queryL,queryR);
        }
        else if (queryR<=mid){
            return query(treeLeftChild,l,mid,queryL,queryR);
        }
        E leftResult = query(treeLeftChild, l, mid, queryL, mid);
        E rightResult = query(treeRightChild, mid + 1, r, mid + 1, queryR);
        return merger.merge(leftResult, rightResult);
    }
    //若数组发生更新，线段树相应做出更新（递归实现）
    public void update(int i,E val){
        data[i]=val;
        updateTree(0,0,data.length-1,i,val);
    }
    private void updateTree(int treeIndex,int l,int r,int i,E val){

        if (l==r){
            tree[treeIndex]=val;
            return;
        }
        int mid=l+(r-l)/2;
        int treeLeftChild=2*treeIndex+1;
        int treeRightChild=2*treeIndex+2;
        if (i<=mid){
            updateTree(treeLeftChild,l,mid,i,val);
        }
        else {
            updateTree(treeRightChild, mid + 1, r, i, val);
        }
        tree[treeIndex]=merger.merge(tree[treeLeftChild],tree[treeRightChild]);

    }
@Override
public String toString(){
    StringBuilder res = new StringBuilder();
    res.append('[');
    for(int i = 0 ; i < tree.length ; i ++){
        if(tree[i] != null)
            res.append(tree[i]);
        else
            res.append("null");

        if(i != tree.length - 1)
            res.append(", ");
    }
    res.append(']');
    return res.toString();
}
}