PID算法优化之积分器抗饱和处理

相关阅读

简易PID算法的快速扫盲（超详细+过程推导+C语言程序）
离散增量式PID算法快速扫描

1 什么是积分饱和

积分饱和（Integral windup或integrator windup）是指PID控制器或是其他有积分器的控制器中可能会发生的一种现象。

这种现象往往发生在误差有大幅变化（例如大幅增加），积分器因为误差的大幅增加有很大的累计量，因为积分器的输出满足下式；
$$K_i{\int }_{{}_0}^{t}e(\tau )d\tau$$
离散化形式表示为：
$$K_i\sum _{i=1}^{k}e(i)\Delta t$$

所以随着时间的增加，每次累积较大的误差$e(i)$，很容易造成积分饱和并产生较大的过冲，而且当误差变为负时，其过冲仍维持一段时间之后才恢复正常的情形。

2 实际的例子

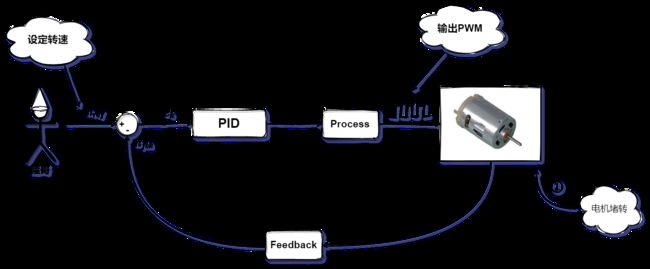
这里举一个直流电机调速例子，先看下图；

• 隆哥设定了转速为$n_{ref}$，这里可以是100 rpm，但是由于某种原因电机一开始堵转了，所以反馈的转速$n_{fbk}$为0；
• 这时候仍然处于堵转状态，那偏差 $e$ 就会一直处于很大的状态，积分器对偏差 $e$ 进行累积，便迅速达到一个很大的值，导致PID的输出已经接近输出的上限，导致最终输出的PWM的占空比很大；
• 此时，堵转忽然消失，但是前面提到PID的输出已经接近输出的上限，因此电机转速也急剧上升，当$n_{fbk}>n_{ref}$时， $e=n_{ref}-n_{fbk}<0$，此时偏差都处于负数状态；
• 虽然误差变成负数，并且积分器开始累加负数，但是由于之前积分器累积的值已经很大，于是，PID依然会保持较大的输出一段时间，从而产生了很大的过冲；

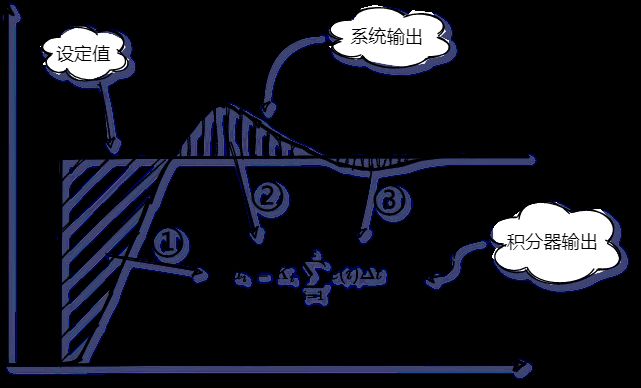
通常会产生的输出如下图所示；

从图中我们不难发现，这里有三个过程；

• 过程①：因为这个过程存在较大幅度变化的误差，因此积分器累积了较大的值，从图中可以看到，积分器的面积比较大（阴影部分）；
• 过程②：此时积分已经饱和，产生了较大的过冲，并且在较长的一段时间内，一直处于过冲的状态；
• 过程③：积分脱离饱和状态，产生了积极的调节作用，消除静差，系统输出达到设定值；

3 负面影响

积分器的作用是消除系统稳态误差，如果出现积分饱和，往往会对系统造成负面的影响；

• 系统输出会产生较大的过冲（超调量）；
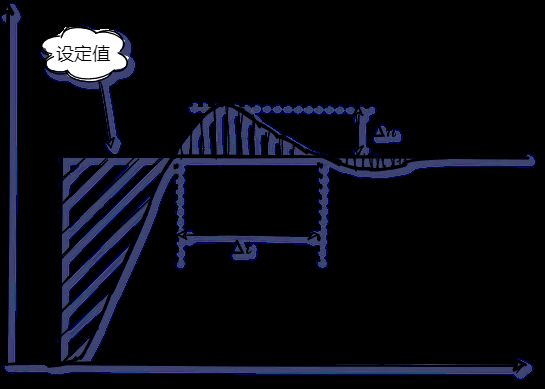
• 如果产生正向饱和（图一所示）则系统对于反向的变化会偏慢；

系统产生了较大的过冲 $\Delta n$，并且较大的一段时间$\Delta t$都处于过冲的状态；
具体如下图所示；

4 如何防止积分饱和

为了防止PID控制器出现积分饱和，需要在算法加入抗积分饱和（anti-integral windup）的算法；通常有以下几种措施；

• 积分分离或者称为去积分算法；
• 在饱和的时候将积分器的累计值初始化到一个比较理想的值；
• 若积分饱和因为目标值突然变化而产生，将目标值以适当斜率的斜坡变化可避免此情形；
• 将积分累计量限制上下限，避免积分累计量超过限制值；
• 如果PID输出已经饱和，重新计算积分累计量，使输出恰好为合理的范围；

下面是TI的位置式PI算法所做的改进，如下图所示；

比例部分的输出：
$$u_p(k)=e(k)=K_p[r(k)-y(k)]$$
积分部分的输出：
$$u_i(k)=u_i(k-1)+K_{i}e(k)$$
未做处理的PID输出：
$$v_1(k)=u_p(k)+u_i(k)$$

最终PID输出 $u(k)$：
$$u(k)=\{\begin{array}{l}{U}_{max}：v_1(k)>U_{max}\\ U_{min}：v_1(k)<U_{min}\\ v_1(k)：U_{min}<v_1(k)<U_{max}\end{array}$$
抗积分饱和用的系数$w_1(k)$
$$w_1(k)=\{\begin{array}{l}0:v_1(k)\ne u(k)\\ 1:v_1(k)=u(k)\end{array}\cdots \cdots ①$$

根据我的理解，由上述输出和①式可知，判断系统是否处于饱和的状态；

如果$v_1(k)\ne u(k)$，说明积分器处于饱和状态，此时使$w_1(k)$系数为0，即是禁用了积分项的输出。

当然，积分抗饱和的方法还有很多，这只是其中的一种，下面给出TI的位置式PID算法，增量式的抗饱和处理也是类似的做法。

5 PID算法（抗饱和）

TI的算法中只实现了比例和积分，如果需要微分项，可以去除结尾部分的注释；

/* ==================================================================================
File name:       PID_REG3.H  (IQ version)                    
=====================================================================================*/

#ifndef __PIDREG3_H__
#define __PIDREG3_H__

typedef struct {
       _iq  Ref;   			// Input: Reference input 
				  _iq  Fdb;   			// Input: Feedback input 
				  _iq  Err;				// Variable: Error
				  _iq  Kp;				// Parameter: Proportional gain
				  _iq  Up;				// Variable: Proportional output 
				  _iq  Ui;				// Variable: Integral output 
				  _iq  Ud;				// Variable: Derivative output 	
				  _iq  OutPreSat; 		// Variable: Pre-saturated output
				  _iq  OutMax;		    // Parameter: Maximum output 
				  _iq  OutMin;	    	// Parameter: Minimum output
				  _iq  Out;   			// Output: PID output 
				  _iq  SatErr;			// Variable: Saturated difference
				  _iq  Ki;			    // Parameter: Integral gain
				  _iq  Kc;		     	// Parameter: Integral correction gain
				  _iq  Kd; 		        // Parameter: Derivative gain
				  _iq  Up1;		   	    // History: Previous proportional output
		 	 	} PIDREG3;	            

typedef PIDREG3 *PIDREG3_handle;
/*-----------------------------------------------------------------------------
Default initalizer for the PIDREG3 object.
-----------------------------------------------------------------------------*/                     
#define PIDREG3_DEFAULTS { 0, 			\
                           0, 			\
                           0, 			\
                           _IQ(1.3), 	\
                           0, 			\
                           0, 			\
                           0, 			\
                           0, 			\
                           _IQ(1), 		\
                           _IQ(-1), 	\
                           0, 			\
                           0, 			\
                           _IQ(0.02), 	\
                           _IQ(0.5), 	\
                           _IQ(1.05), 	\
                           0, 			\
              			  }

/*------------------------------------------------------------------------------
 	PID Macro Definition
------------------------------------------------------------------------------*/


#define PID_MACRO(v)																					\
	v.Err = v.Ref - v.Fdb; 									/* Compute the error */						\
	v.Up= _IQmpy(v.Kp,v.Err);								/* Compute the proportional output */		\
	v.Ui= v.Ui + _IQmpy(v.Ki,v.Up) + _IQmpy(v.Kc,v.SatErr);	/* Compute the integral output */			\
	v.OutPreSat= v.Up + v.Ui;								/* Compute the pre-saturated output */		\
	v.Out = _IQsat(v.OutPreSat, v.OutMax, v.OutMin);		/* Saturate the output */					\
	v.SatErr = v.Out - v.OutPreSat;							/* Compute the saturate difference */		\
	v.Up1 = v.Up;											/* Update the previous proportional output */

#endif // __PIDREG3_H__

// Add the lines below if derivative output is needed following the integral update
// v.Ud = _IQmpy(v.Kd,(v.Up - v.Up1)); 
// v.OutPreSat = v.Up + v.Ui + v.Ud; 

6 参考

https://www.mathworks.com/help/simulink/slref/anti-windup-control-using-a-pid-controller.html

虽然写的不一定是最好，但是每一个字、每一个公式都是用心码的，每一张图都是用心画的，每一句话都是加入了自己的理解，如果帮到了你，请无情三连吧；另外笔者能力有限，文中难免存在错误和纰漏，望轻拍指正。