编程之美7：字符串，那些你必须要会的事。

本系列收录了常见字符串面试和笔试中的八道题，更新于2015年4月23日。
如果有问题或想法，请直接留言，交流。

题目一：字符串移位包含

问题描述：

给定两个字符串s1和s2，要求判定s2是否能够被通过循环移位得到的字符串包含。例如，给定s1 = AABCD和s2 = CDAA，返回true；给定s1 = ABCD和s2 = ACBD，返回false.

问题解答：

解法一：枚举

暴力求解是我们的第一反应，题目要求判定s2是否能被通过循环移位得到的字符串包含，那我们就把s1和它所有的循环移位全部求出来，一个一个判断是否存在字符串包含。话不多说，见代码：

#include   
#include 


using namespace std;  

bool isContain(char *src, char* dest);

void main()  
{  
    char s1[] = "AABCD";
    char s2[] = "CDAA";

    int len = strlen(s1); //总共可移位length-1次
    char temp = s1[len - 1];
    if (isContain(s1, s2))
    {
        cout << "包含" << endl;
        return;
    }

    for (int i = 0; i < len - 1; i++)
    {
        for (int j = len - 1; j > 0; j--)
        {
            s1[j] = s1[j - 1];  
        }
        s1[0] = temp;
        temp = s1[len - 1];

        //一次右移完毕
        if (isContain(s1, s2))
        {
            cout << "包含" << endl;
            return;
        }
    }
    cout << "不包含" << endl;
    system("pause");
} 

bool isContain(char *src, char* dest)
{
    if (NULL != strstr(src, dest))
        return true;
    return false;
}

解法二：规律分析法

我们队循环移位之后的结果进行分析，以s1 = “ABCD”而言，我们将ABCD所有的移位之后的字符串序列写出来，如下所示：
ABCD -> DABC -> CDAB -> BCDA
可以发现，s1及其所有循环移位的序列都是ABCDABCD的子序列。那么如果s2是s1的循环移位子序列，那么s2肯定是s1s1的子序列。那么原题就转换成判断s2是不是s1s1的子序列了，不需要再进行循环移位的操作了。有同学肯定会疑问，属于s1s1的子序列，并不一定是s1循环移位的子序列啊。但是同学们可以试一试，属于s1s1的子序列，并且长度等于或者小于s1的子序列一定是s1的循环移位子序列。那么代码就可以变成：

#include   
#include 


using namespace std;  

bool isContain(char *src, char* dest, int lenSrc, int lenDest);

void main()  
{  
    char s1[] = "AABCD";
    char s2[] = "CDAAF";

    int len1 = strlen(s1); //总共可移位length-1次
    int len2 = strlen(s2);

    if (isContain(s1, s2, len1, len2))
        cout << "包含" << endl;       
    else
        cout << "不包含" << endl;
    system("pause");
} 

bool isContain(char *src, char* dest, int lenSrc, int lenDest)
{
    if (lenDest > lenSrc)
        return false;
    char *doubleSrc = new char[2 * lenSrc + 1]();
    strcpy_s(doubleSrc, 2 * lenSrc + 1, src);
    strcat_s(doubleSrc, 2 * lenSrc + 1, src);
    doubleSrc[2 * lenSrc + 1] = '\0';

    if (NULL == strstr(doubleSrc, dest))
        return false;
    return true;
}

题目二：计算字符串相似度

问题描述：

为计算将str1变换到str2所需最小操作步骤，必须先对变换操作进行定义：

1.修改一个字符（如把“a”替换为“g”）;

2.增加一个字符（如把“abcd”变为“abcdz”）;

3.删除一个字符（如把“travelling”变为“traveling”）;

字符串变换过程中执行了上述三个操作之间的任一操作，则两字符串间距离就加1。例如将上文中的str1变换到str2，即“abcd”到“gbcdz”，通过“abcd”->（操作1）->“gbcd”->（操作2）->“gbcdz”,需进行一次修改和一次添加字符操作，故两字符串距离为2，那么字符串相似度则为距离+1的倒数，即1/3=0.333。这是由俄罗斯科学家Vladimir Levenshtein在1965年提出这个概念。因此也叫Levenshtein Distance。

问题解答：

解法一：递归法

很多时候看起来不知道怎么下手的题目，可以尝试一下递归法。递归法的思想就是把大问题不断转换成小问题。我们看下面一个例子，A=xabcdae和B=xfdfa，先比较第一个元素，相等，那么直接进入到下一个字符的比较。如果不相等，我们可以进行如下的操作，使得这个不相等的字符串相等起来。
操作1：删除A串的第一个字符，然后计算A[1，…, LenA - 1]和B[0, …., LenB - 1]的距离；

操作2：删除B串的第一个字符，然后计算A[0，…, LenA - 1]和B[1, …., LenB - 1]的距离；

操作3：将A的第一个字符修改为B的第一个字符，然后计算A[1，…, LenA - 1]和B[1, …., LenB - 1]的距离；

操作4：将B的第一个字符修改为A的第一个字符，然后计算A[1，…, LenA - 1]和B[1, …., LenB - 1]的距离；

操作5：增加B的第一个字符串到A的第一个字符串前面，然后计算A[0，…, LenA - 1]和B[1, …., LenB - 1]的距离；

操作6：增加A的第一个字符串到B的第一个字符串前面，然后计算A[1，…, LenA - 1]和B[0, …., LenB - 1]的距离；
我们并不在乎具体需要什么操作（删除，修改或添加），我们只关心最后的距离，所以我们将上面六种操作总结一下就是

操作1：一步操作之后，然后计算A[1，…, LenA - 1]和B[0, …., LenB - 1]的距离。比如这个操作可以是删除A串的第一个字符或者是将B的第一个字符修改为A的第一个字符，但是我们不关心具体的操作；

操作2：一步操作之后，然后计算A[0，…, LenA - 1]和B[1, …., LenB - 1]的距离；

操作3：一步操作之后，然后计算A[1，…, LenA - 1]和B[1, …., LenB - 1]的距离；

递归结束的条件：
上面的操作1-操作3只是告诉我们写程序的时候有这么三个分支，递归总是要有退出或者返回条件的啊。所以下面我们讨论一下，这个递归程序几个技术时的情况。
由上面的分析，我们可以大概知道，肯定要传入的参数是，A字符串和B字符串的地址，然后A/B的起始和末尾索引，假设分别为aStartIndex/bStartIndex和aEndIndex/bEndIndex。结束的三种情况：
情况一：A字符串全部遍历完了，那么step保留的是前面操作的步骤，bEndIndex - bStartIndex + 1保留的时候的字符串的距离，所以返回bEndIndex - bStartIndex + step + 1

情况二：B字符串全部遍历完了，那么step保留的是前面操作的步骤，bEndIndex - bStartIndex + 1保留的时候的字符串的距离，所以返回bEndIndex - bStartIndex + step + 1

下面直接看代码吧：

#include 
#include 
#include 

int min2(int a, int b);
int min3(int a, int b, int c);
int calc(char* a, char* b, int aStartIndex, int aEndIndex, int bStartIndex, int bEndIndex, int step);

int main(void)
{
    char *a = "abdd";
    char *b = "aebdd";
    int step = 0;
    printf("%d",calc(a, b, 0, strlen(a) - 1, 0, strlen(b) - 1, step));
    return EXIT_SUCCESS;
}

int calc(char* a, char* b, int aStartIndex, int aEndIndex, int bStartIndex, int bEndIndex, int step)
{
    int d1,d2,d3;
    if (aStartIndex > aEndIndex)
    {
        return bEndIndex - bStartIndex + step + 1;
    }

    if (bStartIndex > bEndIndex)
    {
        return aEndIndex - aStartIndex + step + 1;
    }


    if (a[aStartIndex] == b[bStartIndex])
    {
        //如果该位置处两个字符串的字符相等，那么perfect，直接进入下一个位置的比较
        return calc(a, b, aStartIndex + 1, aEndIndex, bStartIndex + 1, bEndIndex, step);
    }
    else
    {
        step ++;
        d1 = calc(a, b, aStartIndex + 1, aEndIndex, bStartIndex, bEndIndex, step);
        d2 = calc(a, b, aStartIndex, aEndIndex, bStartIndex + 1, bEndIndex, step);
        d3 = calc(a, b, aStartIndex + 1, aEndIndex, bStartIndex + 1, bEndIndex, step);
        return min3(d1, d2, d3);
    }

}

int min2(int a, int b)
{
    return a>b ? b : a;
}

int min3(int a, int b, int c)
{
    if(a > b)
        a = b;
    if(a > c)
        a = c;
    return a;
}

很显然，递归方法最为诟病的就是重复计算的问题，用递归方法的很多都有这个问题。那我们这时候呢，又可以拿出我们的第二把刷子啦，叫做”动态递归法“，动态递归的主要原理就是保存小规模时候程序运行的结果，然后计算大规模数据的时候就可以直接调用小规模的结果了。

解法二：动态递归法

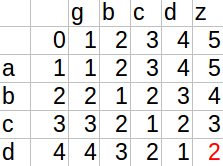
设str1=“abcd”，str2=“gbcdz”，定义一个二维数组d[][]，d[i][j]表示str1中取前i个字符和str2中取前j个字符的最短距离，例如d[3][2]表示“abc”到“gb”的最短距离。

d[i][j]的计算规则有三条：

• 来自d[i - i][j - 1]，即 “str1的前i-1个字符组成的子串” 到 “str2的前j-1个字符组成的子串” 的最小距离，此时如果str1[i] = str2[j]，则最短距离不变，否则最短距离加1（即把str1[i]变为str2[j] ），所以d[i][j] = d[i - 1][j - 1] + (str1[i] == str2[j] ? 0 : 1)
• 来自d[i - 1][j]，即 “A的前i-1个字符组成的子串” 到 “B的前j个字符组成的子串” 的编辑距离。此时删除在A的第i个位置上的字符即可，所以d[i][j] = d[i - 1][j] + 1
• 来自d[i][j - 1], 即 “A的前i个字符组成的子串” 到 “B的前j-1个字符组成的子串” 的编辑距离。此时在A的子串后面添加一个字符B[j]即可，所以d[i][j] = d[i][j - 1] + 1
  于是状态转移方程：d[i][j] = min (d[i - 1][j - 1] + (str1[i] == str2[j] ? 0 : 1) , d[i - 1][j] + 1 , d[i][j - 1] + 1)

例如str1=“abcd”，str2=“gbcdz”的d[][]就为（注意i，j的取值范围）：

代码：

#include 
#include 
#include 
int min(int a, int b, int c);
int calc(char* a, char* b);
int main(void)
{
    printf("%d",calc("abcd", "gbcdz"));
    return EXIT_SUCCESS;
}
int min(int a, int b, int c)
{
    if(a > b)
        a = b;
    if(a > c)
        a = c;
    return a;
}
int calc(char* a, char* b)
{
    int lenA = strlen(a);
    int lenB = strlen(b);
    int **d = new int*[lenA + 1];
    for (int i = 0; i < lenA + 1; i++)
    {
        d[i] = new int[lenB + 1];
    }
    for(int i = 0;i <= lenA; ++i)
        d[i][0] = i;
    for(int i = 0; i <= lenB; ++i)
        d[0][i] = i;
    for(int i = 1; i <= lenA; ++i)
        for(int j = 1; j <= lenB; ++j)
            d[i][j] = min(d[i-1][j-1] + (a[i-1] == b[j-1] ? 0:1), d[i-1][j]+1, d[i][j-1]+1);
    return d[lenA][lenB];
}

题目三：如何输出字符串所有组合和全排列

第一小题：如何输出字符串的所有组合？例如：”abc“输出a、b、c、ab、ac、bc、abc，假设字符串中所有的字符都不重复。

这道题可以位运算来巧妙的解答。假设原有元素 n 个，则最终组合结果是 2n−1 个。我们可以用位操作方法：假设元素原本有：a,b,c 三个，则 1 表示取该元素，0 表示不取。故取a则是001，取ab则是011。所以一共三位，每个位上有两个选择 0 和 1。而000没有意义，所以是 2n−1 个结果。
这些结果的位图值都是 1,2… 2n−1 。所以从值 1 到值 2n−1 依次输出结果：
001,010,011,100,101,110,111 。对应输出组合结果为：a,b,ab,c,ac,bc,abc。
因此可以循环 1~ 2n−1 ，然后输出对应代表的组合即可。有代码如下：

#include 
#include 
#include 

void combination(char *str);
void AllRange(char* str,int start,int length);
void Permutation(char* str);
void Swap(char *a ,char *b);

void main(void)
{
    char src[] = "abc";
    combination(src);
    Permutation(src);
}

//求全组合，如abc的全组合为a b c ab ac bc abc
void combination(char *str)
{
    if (NULL == str)
        return;
    int len = strlen(str);
    int maxN = 1 << len;
    for (int i = 1; i < maxN; i++) //外层循环从1 ~ 2^n - 1
    {
        for (int j = 0; j < len; j++)
        {
            //判断len位的二进制哪一位是1
            if (i & (1 << j))
            {
                printf("%c", str[j]);
            }
        }
        printf(" ");
    }
}

第二小题：如何输出字符串中字符的全排列？例如：”abc“可以输出abc、acb、bac、bca、cab和cba。

所谓全排列，就是打印出字符串中所有字符的所有排列。例如输入字符串abc，则打印出 a、b、c 所能排列出来的所有字符串 abc、acb、bac、bca、cab 和 cba 。
一般最先想到的方法是暴力循环法，即对于每一位，遍历集合中可能的元素，如果在这一位之前出现过了该元素，跳过该元素。例如对于abc，第一位可以是 a 或 b 或 c 。当第一位为 a 时，第二位再遍历集合，发现 a 不行，因为前面已经出现 a 了，而 b 和 c 可以。当第二位为 b 时 ， 再遍历集合，发现 a 和 b 都不行，c 可以。可以用递归或循环来实现，但是复杂度为 O(n^n) 。有没有更优雅的解法呢。

首先考虑bac和cba这二个字符串是如何得出的。显然这二个都是abc中的 a 与后面两字符交换得到的。然后可以将abc的第二个字符和第三个字符交换得到acb。同理可以根据bac和cba来得bca和cab。

因此可以知道 全排列就是从第一个数字起每个数分别与它后面的数字交换，也可以得出这种解法每次得到的结果都是正确结果，所以复杂度为 O(n!)。找到这个规律后，递归的代码就很容易写出来了：

#include
#include

//交换两个字符
void Swap(char *a ,char *b)
{
    char temp = *a;
    *a = *b;
    *b = temp;
}

//递归全排列，start 为全排列开始的下标， length 为str数组的长度
void AllRange(char* str,int start,int length)
{
    if(start == length-1)
    {
        printf("%s\n",str);
    }
    else
    {
        for(int i=start;i<=length-1;i++)    
        {   //从下标为start的数开始，分别与它后面的数字交换
            Swap(&str[start],&str[i]); 
            AllRange(str,start+1,length);
            Swap(&str[start],&str[i]); 
        }
    }
}

void Permutation(char* str)
{
    if(str == NULL)
        return;

    AllRange(str,0,strlen(str));
}

void main()
{
    char str[] = "abc";
    Permutation(str);
}

引申：去重的全排列

如果我们输入的是abb，那么第一个字符与后面的交换后得到 bab、bba。然后abb中，第二个字符和第三个就不用交换了。但是对于bab，它的第二个字符和第三个是不同的，交换后得到bba，和之前的重复了。因此，这种方法不行。
因为abb能得到bab和bba，而bab又能得到bba，那我们能不能第一个bba不求呢？ 我们有了这种思路，第一个字符a与第二个字符b交换得到bab，然后考虑第一个字符a与第三个字符b交换，此时由于第三个字符等于第二个字符，所以它们不再交换。再考虑bab，它的第二个与第三个字符交换可以得到bba。此时全排列生成完毕，即abb、bab、bba三个。
这样我们也得到了在全排列中去掉重复的规则：去重的全排列就是从第一个数字起每个数分别与它后面非重复出现的数字交换。用编程的话描述就是第i个数与第j个数交换时，要求[i,j)中没有与第j个数相等的数。下面给出完整代码：

#include
#include

//交换两个字符
void Swap(char *a ,char *b)
{
    char temp = *a;
    *a = *b;
    *b = temp;
}

//在 str 数组中，[start,end) 中是否有与 str[end] 元素相同的
bool IsSwap(char* str,int start,int end)
{
    for(;startif(str[start] == str[end])
            return false;
    }
    return true;
}

//递归去重全排列，start 为全排列开始的下标， length 为str数组的长度
void AllRange2(char* str,int start,int length)
{
    if(start == length-1)
    {
        printf("%s\n",str);
    }
    else
    {
        for(int i=start;i<=length-1;i++)
        {
            if(IsSwap(str,start,i))
            {
                Swap(&str[start],&str[i]); 
                AllRange2(str,start+1,length);
                Swap(&str[start],&str[i]); 
            }
        }
    }
}

void Permutation(char* str)
{
    if(str == NULL)
        return;

    AllRange2(str,0,strlen(str));
}

void main()
{
    char str[] = "abb";
    Permutation(str);
}

本题参考链接：[http://wuchong.me/blog/2014/07/28/permutation-and-combination-realize/]

题目四：字符串逆序

字符串逆序

给定一个字符串s，将s中的字符顺序颠倒过来，比如s=”abcd”，逆序后变成s=”dcba”。申请一个新的一样长度的空间，然后从字符串尾端逆序复制到新的字符数组这种方法就不说了。一般都要要求原地逆序，也就是不能申请额外的内存空间。那么这个可以用首尾交换法，也很简单。但是交换的时候会用到临时变量，如果要求不能使用临时变量的话，那么可以利用异或操作来完成交换的功能。
异或操作是：相同则为0，不同则为1.如1^1 = 0，而1 ^ 0 = 1。我们假设要交换的两个数为A和B，那么
A = A ^ B
B = A ^ B = ( A ^ B) ^ B = A
A = B ^ A = A ^ (A ^ B) = B
请见代码：

#include 
#include 
#include 

char *reverse1(char *src);
char *reverse2(char *src);

void main(void)
{
    char src[] = "aba";
    //printf("%s \n", reverse1(src));
    printf("%s \n", reverse2(src));
}

//原地逆序方法一：首尾进行交换
char *reverse1(char *src)
{
    int len = strlen(src);
    char temp;
    for (int i = 0; i < len/2; i++)
    {
        temp = *(src + i);
        *(src + i) = *(src + len - 1 - i);
        *(src + len - 1 - i) = temp;
    }
    return src;
}

//原地逆序方法二：不使用临时变量来交换
char *reverse2(char *src)
{
    int len = strlen(src);
    char temp;
    for (int i = 0; i < len/2; i++)
    {
        *(src + i) = (*(src + i)) ^ (*(src + len - 1 - i));
        *(src + len - 1 - i) = (*(src + i)) ^ (*(src + len - 1 - i));
        *(src + i) = (*(src + i)) ^ (*(src + len - 1 - i));
    }
    return src;
}

按照单词逆序

给定一个字符串，按单词将该字符串逆序，比如给定”This is a sentence”，则输出是”sentence a is This”，为了简化问题，字符串中不包含标点符号。
解法：当然如果这道题会用c++的话，很简单，把每一个单词都存进一个vector或者map，然后逆序输出。当然这种解法肯定不是我们需要讨论的问题。我们要做的就是回归原始。
分两步

1 先按单词逆序得到”sihT si a ecnetnes”

2 再整个句子逆序得到”sentence a is This”
见代码：

#include 
#include 
#include 

char *reverse2(char *src, int start, int end);
char *reverseWords(char *src);

void main(void)
{
    char src[] = "This is a sentence";
    printf("%s \n", reverseWords(src));
}

char *reverseWords(char *src)
{
    int start = 0;
    //先一个一个单词来逆序
    for (int i = 0; i <= strlen(src); i++)
    {
        if (src[i] == ' ' || i == strlen(src))
        {
            src = reverse2(src, start, i - 1);
            start = i + 1;
        }       
    }
    //后面整个句子逆序
    return reverse2(src, 0, strlen(src) - 1);
}

//原地逆序方法二：不使用临时变量来交换
char *reverse2(char *src, int start, int end)
{
    if (end == start)
        return src;
    for (int i = start; i <= (start + end) / 2; i++)
    {
        *(src + i) = (*(src + i)) ^ (*(src + start + end - i));
        *(src + start + end - i) = (*(src + i)) ^ (*(src + start + end - i));
        *(src + i) = (*(src + i)) ^ (*(src + start + end - i));
    }
    return src;
}

题目五：如何统计一行字符串中有多少个单词？

太简单，直接看代码。

#include 
#include 
#include 

int getWordsCount(char *src);

void main(void)
{
    char src[] = "This is a sentence";
    printf("%d \n", getWordsCount(src));
}

int getWordsCount(char *src)
{
    int result = 0;
    int forStartIndex = 0;

    //去除一行开头的空格
    for (int i = 0; i < strlen(src); i++)
    {
        if (src[i] != ' ')
        {
            forStartIndex = i;
            break;
        }
    }

    for (int i = forStartIndex; i < strlen(src); i++)
    {
        //如果当前位为空格，且下一位是字符
        if (src[i] == ' ' && src[i + 1] != ' ')
            result++;
    }
    //单词数目 = 空格数目 + 1
    return result + 1;
}

题目六：自己编写字符串库函数strcpy()。

使用下面代码一个需要注意的问题就是，当目的字符分配的空间大于源字符分配的空间时，拷贝之后，目的字符的长度会减小，请见代码str拷贝到dst2。

#include 
#include 
#include 
#include 
#include 

char* strcpyOwn(char *strDest, const char* strSrc);

void main(void)
{
    char *src = "Hello world";
    char dst1[] = "goo";
    char dst2[] = "good night, guys";
    printf("%s\n", strcpyOwn(dst1, src));
    printf("%s\n", strcpyOwn(dst2, src));
}

//自己实现字符串拷贝函数
char *strcpyOwn(char *strDest, const char *strScr)
{
       char *address=strDest;
       assert((strDest != NULL) && (strScr != NULL));
       while(*strScr != '\0' && *strDest != '\0') 
       {
              *strDest++ = *strScr++;
       }
       *strDest = '\0';                       
       return address;
}

题目七：如何找出一个字符串中第一个只出现一次的字符

不解释，太简单，看代码

#include 
#include 
#include 

char getFirstAppearOnceChar(char *src);

void main(void)
{
    char src[] = "ThhiTs##%is a sentence";
    printf("%c \n", getFirstAppearOnceChar(src));
}

//找出第一个只出现一次的字符
char getFirstAppearOnceChar(char *src)
{
    //因为ASCII码只有127个，那么我们将申请一个长度为128的int型数组，用来记录每个ASCII码出现的次数
    int *times = new int[128]();
    for (int i = 0; i < strlen(src); i++)
    {
        times[src[i] - NULL]++;
    }

    //再次遍历原字符串数组，选出第一个出现一次的字符
    for (int i = 0; i < strlen(src); i++)
    {
        if (1 == times[src[i] - NULL])
            return src[i];
    }
}

题目八：字符转整数

这道题目需要注意的细节比较多，总结一下：

• 非法字符问题
• 如果存在非法字符，怎么处理？返回什么？
• 第一个字符如果是”+“号或者”-“，怎么处理？
• 溢出的问题怎么处理？
• 溢出问题上，正数和负数能表示的极限值是不一样的，处理上会有不同吗？

带着这些问题，小伙伴们看代码吧。关键地方我都有写注释，哪里有问题请留言哈！

代码：

#include 
#include 
#include 
#include 

bool strToInt(const char* src, int *num);
bool isValidChar(char cBit);

void main(void)
{
    char src[] = "-2147483648";
    int result = 0;
    if (false == strToInt(src, &result))
        printf("转换失败，请检查是否有非法字符或者是否存在溢出问题！\n");
    else
        printf("%d \n", result);
}

//字符串转整数
bool strToInt(const char* src, int *num)
{
    int bitInt = 0; //每一位字符对应的整数
    bool isSmallerThanZero = false; //是否是复数
    int forStartIndex = 0;

    //先处理字符串的第一个字符，判断是不是正负号
    if (src[0] == '-')
    {
        isSmallerThanZero = true;
        forStartIndex = 1;
    }
    else if(src[0] == '+')
    {
        forStartIndex = 1;
    }
    else if(!isValidChar(src[0]))
    {
         return false;
    }

    for (int i = forStartIndex; i < strlen(src); i++)
    {

        if (false == isValidChar(src[i]))
            return false;
        bitInt = src[i] - '0';
        //因为负数溢出的范围和正数溢出的范围不一样，所以要分开处理。如int型表示的整数的范围为-2^31 -> 2^31
        if (false == isSmallerThanZero)
        {
            if ((*num) * 10 > INT_MAX - bitInt)         
                return false; //再接下去会溢出，直接返回false;      
            (*num) = (*num) * 10 + bitInt; //不会溢出
        }
        else
        {
            if ((*num) * 10 < INT_MIN + bitInt)
                return false;
            *(num) = (*num) * 10 - bitInt;
        }
    }

    return true;
}

//判断是否是非法字符,只判断是否是0-9
bool isValidChar(char cBit)
{
    if (cBit < '0' || cBit > '9')
        return false;
    return true;
}