编辑本段概述
李德毅老师开创的"云"理论,是对传统的隶属函数概念的扬弃。自然界中大量模糊概念可以用正态云来刻划的事实,导致了对正态云外部特征以及内部机理的深入研究。模糊概念可表述为一个边界具有不同弹性的,收敛于正态分布函数的"云"。实质上,云是用语言值表示的某个定性概念与其定量表示之间的不确定性转换模型,云的数字特征可用期望值Ex、熵En、超熵He三个数值来表征,它把模糊性和随机性完全集成到一起,构成定性和定量相互间的映射,为定性与定量相结合的信息处理提供了有力手段。所以它成为令人瞩目的处理模糊信息的有效工具。
什么是“云”
云是用语言值表示的某个定性概念与其定量表示之间的不确定转换模型,它主要反映宇宙中事物或人类知识中概念的两种不确定性:模糊性(边界的亦此亦比性)和随机性(发生的概率),用云模型把模糊性和随机性完全集成在一起,研究自然语言中的最基本的语言值(又称语言原子)所蕴含的不确定性的普遍规律,使得有可能从语言值表达的定性的信息中获得定量数据的范围和分布规律,也有可能从精确数值有效转换为恰当的定性语言值。
对“云”的描述
设X是一个精确数值量的集合X={x},称为论域,关于论域X上对应的定性概念 ,是指对于任意数值量,都存在一个有稳定倾向的随机数 ,叫作x对的隶属度,隶属度在论域上的分布称为隶属云,简称为云,它由许许多多云滴组成,某一个云滴也许无足轻重,但云的整体形状反映了定性概念的重要特性。因为这种分布很类似天空中的云彩,远看有明确的形状,近看没有确定的边界,所以借用云来比喻定性和定量之间的不确定性映射。
云的数字特征
不确定性的概念的整体特性可以用云的数字特征来反映,这是定性概念的整体定量特性,对于理解定性概念的内涵和外延有着重要的意义。
①云的期望
Ex(Expected value),云滴在论域空间的分布期望,就是最能代表定性概念的点,也是这个概念量化的最典型样本。
②熵
En(Entropy),定性概念的不确定性度量,由概念的随机性和模糊性共同决定。一方面
En是定性概念随机性的度量,反映了能够代表这个定性概念的云滴的离散程度;另一方面又是定性概念亦此亦彼性的度量,反映了论域空间中可被概念接受的云滴的取值范围。
③超熵
He(Hyper entropy),超熵是熵的不确定性的度量,即是熵的熵,由熵的随机性和模糊性共同决定。
编辑本段一维正态云模型
模型描述
云模型是云的具体实现方法,也是基于云的运算、推理和控制等的基础,由定性概念到定量表示的过程,也就是有云的数字特征产生云滴的具体实现,称为正向云发生器;由定量表示到定性概念的过程,也就是由云滴得到云的数字特征的具体实现,称为逆向云发生器。
由于在概率论与随机过程的理论研究和实际应用中,正态分布起着特别重要的作用,在各种概率分布中居于首要的地位,其概率分布的形式广泛存在于自然现象、社会现象、科学技术以及生产活动中,,在实际中遇到的许多随机现象都服从或近似服从正态分布。而且,中心极限定理也在理论上阐述了产生正态分布的条件,体现了其的广泛性和普适性。
另外,在模糊集理论中,隶属函数是模糊理论的基石,但自然和社会科学中的大量模糊概念的隶属函数,并没有严格的确定方法,在通常的经验下最为常见的隶属函数是钟形隶属函数,这与正态分布的分布函数的一致的。
模型模拟
以一般来讲,以正态云模型作为代表,是具有普遍性的。而且从介绍简单起见,我们介绍一维正态云模型,如图所示。此图由数字特征(0, 3, 0.3),以及10000个云滴生成。
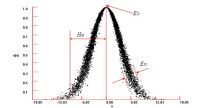
一维正态云模型
编辑本段云发生器
云发生器是从定性概念到定量表示的过程,也就是有云的数字特征产生云滴的具体实现。下面具体说明正向及逆向正态云发生器以及
X云发生器和
Y云发生器。
正向正态云发生器
当概念对应的数域为一维时,正态云发生器的算法如下:
(
Ex,
En,
He)→
Drop (
x, y)
X云发生器和Y云发生器
X云发生器和
Y云发生器就是指在已知云的三个数字特征(
Ex,
En,
He)的前提下,还已知特定的
x=x0或者
y=y0条件,所以也叫
X条件云发生器和
Y条件云发生器,由于
y=y0表示已知的是特定的隶属度,
Y条件云发生器也叫做隶属度条件云发生器,
X条件云发生器和
Y条件云发生器是基于云模型的不确定性推理的基础,比如将
X条件云与
Y条件云相连接就构成了一个单条件规则发生器。
逆向云发生器
所谓逆向云发生器是指从定量表示到定性概念的过程,也就是由云滴得到云的数字特征的具体实现,如下所示:
(
x1, y1),(
x2, y2),(
x3, y3)……
→(
Ex,
En,
He)
编辑本段分类
按云的产生机理和计算方向有以下分类:
云的应用范围很广,目前云模型被成功地用于人工智能、跳频云发生器、C3I系统的效能评估中。