R中矩阵的奇异值分解SVD

   

   Singular Value Decomposition(SVD),奇异值分解是一种具有重要实际应用意义的矩阵分解方式，已经具有很广泛的应用，如压缩存储，矩阵求秩，确定投影算子等。

   通常存储矩阵值是按行或者列存储矩阵的每一个值，奇异值分解的结果可作为一种存储矩阵值的另一种方式。奇异值分解将矩阵进行等价变换，将矩阵所存储的值分散在不同的变量中，包括奇异值，左奇异向量，右奇异向量,在没有略去部分奇异值项的条件下，可以通过特定的方式还原矩阵的全部信息。这种方式能够很有效地节省所需的存储空间(内存空间或者磁盘空间)，同时，可在精度允许范围内略去奇异值分解结果中一些小的奇异值对应的项，这样在满足要求的条件下将节省更多的存储空间。

   以下例子是本人用R实现的SVD分解的实例，首先利用R中的函数对给定数据进行SVD分解，然后根据SVD的定义用SVD分解的结果还原原矩阵，同时还涉及到了略去部分小奇异值项后，原矩阵和新矩阵之间的平均绝对偏差。

   

  本例中的数据temp.csv:

A,B,C,D
71,74,92,79
77,73,62,70
80,84,95,88
78,83,82,88
75,82,96,77
66,84,70,79
70,83,66,70
78,84,70,29
72,87,78,49
79,85,79,80

  R实现SVD分解的代码:

inputdata <- read.csv("temp.csv", sep = ",", header = T)
svdresults <- svd(inputdata, nu = min(nrow(inputdata), ncol(inputdata)), 
                 nv = min(nrow(inputdata), ncol(inputdata)), LINPACK = F)

#创建初始值为0矩阵，用来从svd的参数中还原原矩阵
svd2matrix <- matrix(0, nrow = nrow(inputdata), ncol = ncol(inputdata)) 

#可以尝试略去一些奇异值较小的项
ignorenum <- 0  #设置去掉一些最小奇异值的个数
for (i in 1:(length(svdresults$d) - ignorenum))
{
    svd2matrix <- svd2matrix + svdresults$d[i] * as.matrix(svdresults$u[, i]) %*% t(as.matrix(svdresults$v[, i])) 
}

#求平均绝对偏差，通过平均绝对偏差来衡量整体信息的还原程度
colME <- NULL    
for (j in 1:length(svdresults$d))
{
    #求每一列的绝对偏差的和
    colME <- c(colME, sum(abs(svd2matrix[, j] - inputdata[, j])))
}

#根据每一列总和来计算平均绝对偏差
meanME <- sum(colME) / (nrow(inputdata) * ncol(inputdata))

   运行结果:

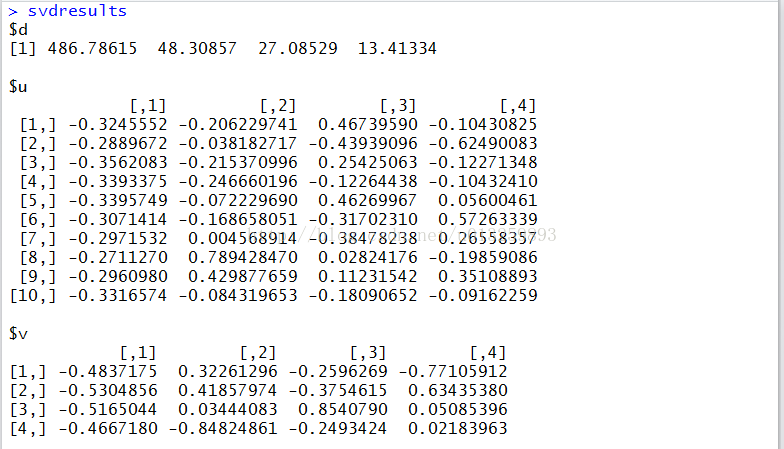
  1).对temp.csv中的数据利用SVD分解后的结果:

  

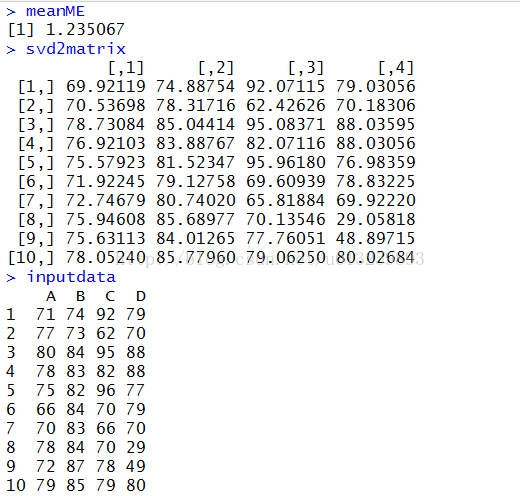
 2).略去奇异值最小的一项(在代码中修改ignorenum<-1，然后重新运行代码)后，平均绝对偏差、还原后的矩阵以及原矩阵分别如下: