GYM 100923 G解题思路分析
题目大意:
给出一个N*M的矩阵,矩阵中每个格点具有可正可负的权值,求出权值最大的联通块的权值和。
思考过程:
从一开始就想的一直是多维dp,因为题中给出的是一个矩阵。但是多维dp又只能求出一条“路径”而不是一个联通块,因此又想到了dp之后再搜索合并“路径”,但是实在没有不TLE的实现方法,于是开始觉得情况不是我想象的这样。
然后又套用矩阵中取子矩形的方式进行下一轮的思考,但是也同样,因为联通块是不规则的,所以这种做法会丢掉一些联通块和一些带负权的格点。
经过启发,一个新的思路出现了——区间dp。我在听到可以用区间dp来解决这道题的时候,一下就脑补到可以将某一行中一定范围内可取的权值最大的区间合并到下一行中可进行合并的区间里面。但是实现也成为了问题:如何表示区间、如何计算复合某种条件的区间中的最大的权值、如何转移状态等等。
解读代码:
在solve()函数中,首先将矩阵读入。然后以行为单位,处理出row_pref[i][j]数组——既矩形中的第i行第1列到第i行第j列的和。然后正序处理出row_min[i][j]数组——既第i行从第1列到第i列的最小连续权值和;再倒序处理出row_max[i][j]数组——既第i行从第n列到第i列的最大连续权值和。在处理好row_min和row_max数组之后,通过第一页的 get_best(int i,int j,int k)函数得到在第i行中包含着从第j列到第k列(图中的定位标识)的连续列的最大权值和,在get_best中得到这个值的过程非常的巧妙: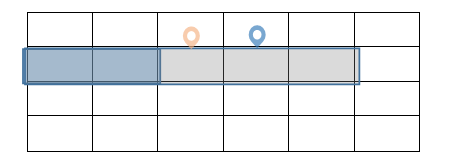
如果把想要得到的区间用[L,R]来表示的话,由于row_max数组是倒序处理的,所以就可以保证R>=r,即上图中的灰色窗口;又因为row_min数组是正序处理的,所以就可以保证L<=l,即上图中的蓝色窗口。从而就可以得出包含着[j,k]的最大权值区间的权值(被灰色窗口覆盖但是没有被蓝色窗口覆盖的部分)。
下一步就是观察dp的状态,在预处理状态的时候我们就可以发现它调用了get_best函数且j和k相同。则预处理之后我们可知dp[i][j]的含义为——第i行包含第j列的区间的最大权值。设计好状态我想大家就已经知道状态要如何进行转移了:首先,在同一行中,dp状态的处理就已经保证了该区间内的各个格点都是相连的了;然后就可以分析如何实现行与行之间的累加的转移,想要从一行转移到下一行就必须要保证两行所选的区间之间要有公共的列,换句话说就是想要把两行的区间合并为一个联通块就必须要保证两个联通块是相接的。
状态转移方程中的int new_val = val + get_best(i + 1, j, k);一句就已经说道了状态转移的精髓,我认为这也是这道题的点睛之笔。一个get_best(i + 1, j, k)就保证了两行之间在选择了j和k所在的最优区间之后的联通。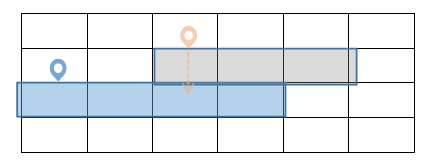
这就像j和k本来一上一下,谁也碰不到谁,但是只要在下面的那一行的k“伸”出来一个保证能“接到”j的区间(即第i+1行中包含着[j,k]的区间),就能保证下面的区间可以和上面的那个区间合并在同一个联通块中。也就是说,这样的值就可以用来累加并更新答案了。
思路启发:
这道题告诉我在多维空间下进行dp不一定就要进行多维dp,而且要更加仔细和认真地分析题目中的数据:比如这道题的数据就是1<=N,M<=300,可知复杂度在O(n^3) or O(n^2logn)左右的算法就可以解出此题。一开始分析题目的时候思路实在是太过的局限了,才会导致把思路困在一个错误的方向长达三天之久。同时还要更加深入的去理解题目,更重要的是,对于那种已知在状态转移或者预处理的时候所需要处理的参数,要更注重这部分的处理的技巧,这道题了get_best函数就是一个很好的例子。