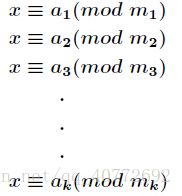ACM数论----中国剩余定理与拓展中国剩余定理

一.问题引入：

在《孙子算经》中有这样一个问题：“今有物不知其数，三三数之剩二（除以3余2），五五数之剩三（除以5余3），七七数之剩二（除以7余2），问物几何？”这个问题称为“孙子问题”，该问题的一般解法国际上称为“中国剩余定理”。（壮哉我大中华）

这个问题如何求解呢？来看一我一步步推导：

1.假设 n1 % 3 = 2 , n2 % 5 = 3 , n3 % 7 = 2 ;那么如果要使, (n1 + n2) % 3 = 2,那么就要求 n2 也是 3 的倍数 ， 那么如果要使, (n1 + n3) % 3 = 2,那么就要求 n3 也是 3 的倍数 ， 那么如果要使, (n1 + n2 + n3) % 3 = 2,那么就要求 n2和n3 都是 3 的倍数，这是在n1的角度上说的，于是有为了使 （n1 + n2 + n3）成为这样的数字，就要：

（1）（n1 + n2 + n3）%3 = 2成立：n2 和 n3 是 3 的倍数。

（2）（n1 + n2 + n3）%5 = 3成立：n1 和 n3 是5的倍数。

（3）（n1 + n2 + n3）%7 = 2成立：n1 和 n2 是7的倍数。

所以，为了使（n1 + n2 + n3）成为问题的答案，我们需要：

（1）n1 % 3 =2 并且 n1 是 5 和 7 的公倍数

（2）n2 % 5 = 3并且 n2 是 3 和 7 的公倍数

（3）n3 % 7 = 2并且 n3 是 3 和 5 的公倍数

所以，孙子问题解法的本质是从5和7的公倍数中找一个除以3余2的数n1，从3和7的公倍数中找一个除以5余3的数n2，从3和5的公倍数中找一个除以7余2的数n3，再将三个数相加得到解。

这里在求n时采用了一个小技巧：假设 a % p = c, 那么（a + a）%p = （a%p + a%p） = 2c;所以这里我们求n1的时候先求 n % 3=1的解，然后n1 = n*2 ,以此类推。（因为这样就能用上逆元了，5*7 x = 1（mod 3），所以 n1 =（5*7x ）*2 =  5*7*inv（5*7）%3*2）；

因此最小正整数解 n = （n1 + n2 + n3）%（n1 n2 n3 的最小公倍数） = 23；

二.中国剩余定理

假设m1 , m2 , m3 .......互质，并且有下列的同余方程：

 

有解x = （n1 + n2 + n3 + n4 + ..... + nk）%（m1,m2...mk的最小公倍数）

因为m1 , m2 , m3 , .....mk是互质的 ， 所以最小公倍数M = m1 * m2 * m3 * .....*mk 

而 n1 = m2 * m3 * .....* mk * inv（m2 * m3 * ....* mk）%m1 * a1 = M/m1 * inv（M/m1）%m1 * a1;

以此类推，故而得出最小正整数解：

x = （a1*M1*inv（M1） + a2 * M2 * inv（M2） + .... + ai * Mi * inv（Mi） + ... + ak*Mk*inv（Mk））%M;

其中：Mi = M/mi ; inv（Mi） 为 Mi 模 mi 的逆元。

 

三.板子代码

#include 
#include 
#include
#include
using namespace std;
typedef long long LL;
const int maxn = 100000 + 10;
LL a[maxn],m[maxn],n;
LL ex_gcd(LL a,LL b,LL &x,LL &y){//拓展欧几里得
    if(b==0){x = 1;y = 0;return a;}
    LL ans = ex_gcd(b,a%b,x,y);
    LL temp = x;
    x = y;
    y = temp - a/b*y;
    return ans;
}
LL inv(LL a,LL b){//求逆元
   LL x,y;
   LL ans = ex_gcd(a,b,x,y);
   if(ans!=1)return -1;
   if(x<0)x = (x%b + b)%b;
   return x;
}
LL China(){//中国剩余定理
   LL M = 1;
   for(int i = 0;i

 

四.切一发水题

poj 1006 Biorhythms

题意：人自出生起就有体力，情感和智力三个生理周期，分别为23，28和33天。一个周期内有一天为峰值，在这一天，人在对应的方面（体力，情感或智力）表现最好。通常这三个周期的峰值不会是同一天。现在给出三个日期，分别对应于体力，情感，智力在今年出现峰值的日期。然后再给出一个起始日期，要求从这一天开始，算出最少再过多少天后三个峰值同时出现。

分析：假设x为这个天数，n1为第一个周期出现的日期，p1为其周期，以此类推，则如果同时出现峰值，则：

x = n1 + k1*p1

x = n2 + k2*p2

x = n3 + k3*p3

两侧同时取余p有：

x%p1 = n1%p1即 x % p1 = a1

x%p2 = n2%p2即x % p2 = a2

x%p3 = n3%p3即x % p3 = a3

并且p1 = 23,p2 = 27,p3 = 33两两互质可以使用中国剩余定理！

就是就同时满足这三个式子的x，跟引入同样的题目，但是注意求出x后减去初始日期，还要注意如果求出来x<初始日期要加上三个周期的倍数（让你计算下一个周期）

代码：

#include 
#include
#include
#include
#include
using namespace std;
int m[3],a[3];
int M;
int ex_gcd(int a,int b,int &x,int &y){//拓展欧几里得
    if(b==0){x = 1;y = 0;return a;}
    int res = ex_gcd(b,a%b,x,y);
    int temp = x;
    x = y;
    y = temp - a/b*y;
    return res;
}
int inv(int a,int b){//求逆元
   int x,y;
   int ans = ex_gcd(a,b,x,y);
   if(ans!=1)return -1;
   if(x<0)x = (x%b + b)%b;
   return x;
}
int China(){//中国剩余定理
    int sum = 0;
    for(int j = 0;j<3;j++){
        int res = M/m[j];
        sum = (sum + a[j]*res*inv(res,m[j]))%M;
    }
    return sum;
}
int main()
{
    int initial;
    int t = 0;
    m[0] = 23;m[1] = 28;m[2] = 33;
    M = 1;
    for(int i = 0;i<3;i++)M*=m[i];//公倍数
    while(scanf("%d%d%d%d",&a[0],&a[1],&a[2],&initial)!=EOF){
        t++;
        if(a[0]==-1&&a[1]==-1&&a[2]==-1&&initial==-1)break;
        for(int i = 0;i<3;i++)a[i]%=m[i];//求a[i]
        int ans = China();
        if(ans<=initial)ans+=21252;
        printf("Case %d: the next triple peak occurs in %d days.\n",t,ans-initial);
    }
    return 0;
}

 

五.拓展中国剩余定理EX_CRT

（1）上述解决是在模数两两互素的条件下进行的，那么现在如果不两两互素呢？

证明如下：

 

（2）代码：（引入快速乘）

#include 
#include
using namespace std;
typedef long long LL;
const int maxn = 100000 + 7;
LL C[maxn],M[maxn];
int n;
LL gcd(LL a,LL b){
     return b==0?a:gcd(b,a%b);
}
LL ex_gcd(LL a,LL b,LL &x,LL &y){
   if(b==0){x = 1;y = 0;return a;}
   LL g = ex_gcd(b,a%b,x,y);
   LL temp = x;
   x = y;
   y = temp - a/b*y;
   return g;
}
LL inv(LL a,LL mod){
   LL X,Y;
   LL g = ex_gcd(a,mod,X,Y);
   if(g!=1)return -1;
   return (X%mod + mod)%mod;
}
LL mul(LL a,LL b,LL mod){//快速乘法
   LL ans = 0;
   //cout<>=1;
      a = (a%mod + a%mod)%mod;
   }
   return ans;
}
int main()
{
    while(scanf("%d",&n)!=EOF&&n){
        for(int i = 0;i

（3）水题 HDU1573

 注意 ： 余数为零（整除的坑点！）

#include 
#include
using namespace std;
typedef long long LL;
const int maxn = 20+ 7;
LL M[maxn],C[maxn],n,m;
LL gcd(LL a,LL b){
   return b==0?a:gcd(b,a%b);
}
LL ex_gcd(LL a,LL b,LL &x,LL &y){
    if(b==0){x = 1;y = 0;return a;}
    LL g = ex_gcd(b,a%b,x,y);
    LL temp = x;
    x = y;
    y = temp - a/b*y;
    return g;
}
LL inv(LL a,LL mod){
   LL X,Y;
   LL g = ex_gcd(a,mod,X,Y);
   if(g!=1)return -1;
   return (X%mod + mod)%mod;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%lld%lld",&n,&m);
        for(int i = 0;in){printf("0\n");continue;}
        LL ans = (n - C[m-1])/M[m-1] + 1;
        if(C[m-1]==0)ans--;//x = k*M[m-1],求正整数，不包括0！！
        printf("%lld\n",ans);
    }
    return 0;
}