算法与结构--选择排序

为什么要学习算法

万事万物皆算法，Linus大神曾说过：“低水平程序员总在考虑代码,高水平程序员总在考虑数据结构及其之间的关系”。其实现实中无时无刻在接触算法，只不过很多算法被封装起来而没有在意，如果一味地写逻辑而不去考虑算法优化是不会有什么提高的。现在技术日新月异，我认为唯一能让你在以后的竞争中脱颖而出的就是算法。
算法系列文章打算从简单的排序开始，此后逐渐升级，并且我们会分析此排序的优缺点，适应场景，并且会尝试优化排序，并给出测试用例。本节我们先简单分析下选择排序
一切的始源与终点皆为思想。

公共方法

在开始算法之前，我们先写一个辅助类，以后的辅助方法都会在此基础上添加或升级；方法如下

import java.util.Arrays;
import java.util.Random;

/**
 * 算法辅助类
 *
 * @author wangmj
 * @since 2019/3/13
 */
public class SortHelper {

    /**
     * 生成个数为n,范围在[min~max]之间的数组
     *
     * @param n   数组个数
     * @param min 最小数
     * @param max 最大数
     * @return 随机数组
     */
    public static int[] generateArr(int n, int min, int max) {
        assert min <= max;
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            Random random = new Random();
            int value = random.nextInt(max - min) + min + 1;
            arr[i] = value;
        }
        return arr;
    }

    /**
     * 打印数组
     *
     * @param arr 数组
     */
    public static void printer(int arr[]) {
        System.out.println(Arrays.toString(arr));
    }

    /**
     * 交换数组元素
     *
     * @param arr    数组
     * @param before 交换位置1
     * @param after  交换位置2
     */
    public static void swapArr(int[] arr, int before, int after) {
        int beforeVal = arr[before];
        arr[before] = arr[after];
        arr[after] = beforeVal;
    }
}

此辅助类主要包含三个方法，生成随机数组、交换两个元素、打印数组，很简单。

选择排序

什么是选择排序，顾名思义就是每次遍历选择最小的那个然后放到头位置，然后下次遍历再次找到最小的元素放在第二个位置，以此类推，就成为了一个有序的数组。看下面的动图，可以清晰地看到他的时间复杂度为o(n2)。

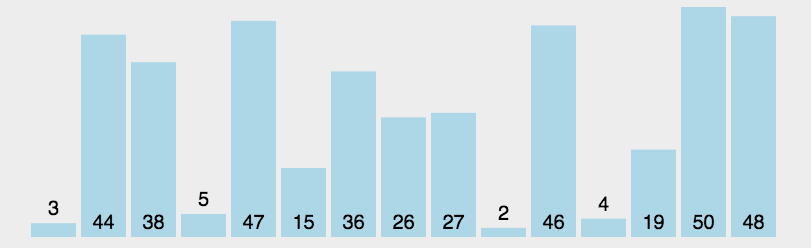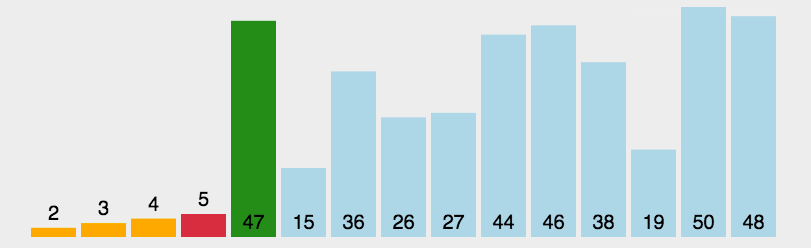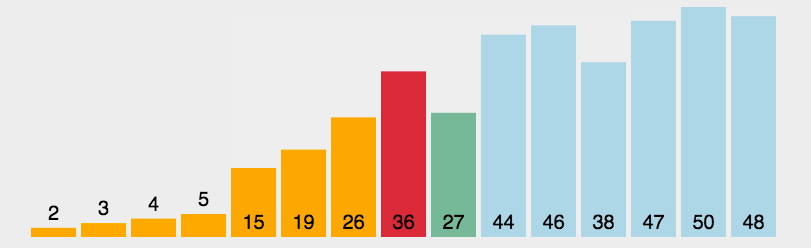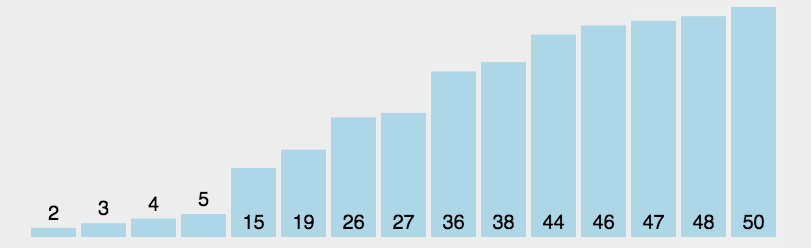
理解了思想代码就简单了

/**
 * 选择排序
 *
 * @author wangmj
 * @since 2019/3/13
 */
public class SortTest {
    public static void main(String[] args) {
        //随机生成区间内的正整数
        int[] arr = SortHelper.generateArr(10000, 2, 30000);

        //选择排序
        long start = System.nanoTime();
        selectionSort(arr);
        long endTime = System.nanoTime();
        System.out.println("selection time = " + TimeUnit.NANOSECONDS.toMillis(endTime - start));
        SortHelper.printer(arr);
    }

    /**
     * 选择排序
     *
     * @param arr 数组
     */
    private static void selectionSort(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            int minIndex = i;
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[minIndex] > arr[j]) {
                    minIndex = j;
                }
            }
            SortHelper.swapArr(arr, i, minIndex);
        }
    }


}

我们看下结果

selection time = 103
[9, 13, 13, 16, 20, 21, 22, 24, 26, 31, 32, 45, 46, 47, 47, 50, 51, 52, 54, 56, 59, 60, 76, 78, 78, 81, 84, 84, 87, 91, 91, 93, 97...]

看到排序10000个随机数时间大概是103ms。

总结

选择排序的时间复杂度为O(n2)，他的优点是交换次数较少(最多只需要交换n次)，相对于遍历交换数组中元素更加耗费时间，他的缺点也很明显，就是复杂度为n2，且基本不能优化