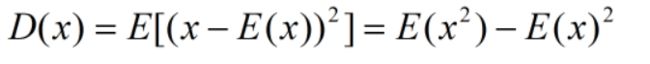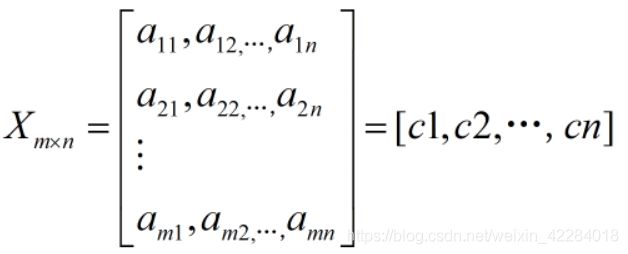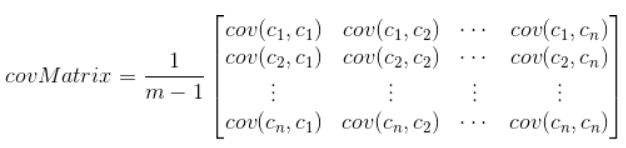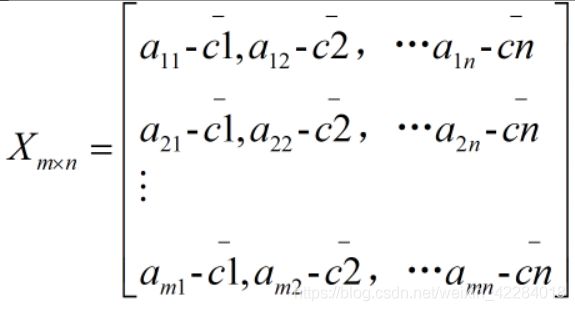概率论与统计学基础-------------各种名称含义、用途、几何意义
1.随机变量：X。随机变量的产生具有概率性，且具有多种可能产生的情况。可以看成一个事物的特征、属性。
2.CDF 累积分布函数：F(x)；PDF积分；CDF的反函数可以得到服从CDF分布的随机变量；F(b)-F(a)=P(a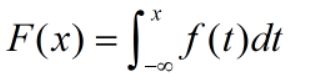
3.PDF概率密度函数：f(x);主要描述连续的随机变量；它的积分才是概率；曲线形状的峰值为随机变量的期望；胖瘦对应对X的方差；整体曲线下面积值为1；
4.PMF概率质量函数：主要描述离散的随机变量；它的值是特定情况a或者b发生的概率。p(a)=P(X=a);
CDF、PDF、PMF这些函数可以描述随机变量。我们大多数关注随机变量发生的概率，以及在某区间内发生的概率。我们实际获得的都是离散类的数据，在机器学习中，数据可以进行分类，那么同一类别的数据可以看成服从同一种概率分布，用函数分类很困难，用常量数字特征分类很轻松。因此，对于服从一种特定PDF曲线形状的随机变量，具有特定的数字特征，这些数字特征也可以代替函数来描述随机变量，例如期望、方差、协方差等。
5.期望E：变量；随机变量可能取值的加权平均，权重就是该取值的概率p(x)；当各个随机情况概率相等的时候，期望大小等于平均值;
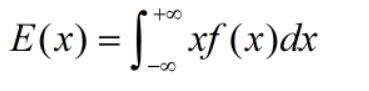；大多数情况下我们不能计算出期望，因为我们不知道数据发生的概率以及它的PDF。
6.大数定理（主要适用于信号处理，图像处理）：很大数量的样本，会出现一个规律，期望值并不是变量了，它等于常量均值；因此我们会经常看到信号处理，图像处理中，求数据的期望，直接求的是平均值（若是小样本会有偏差）；因为我们总不能得到无限的大量的样本数据，只能得到小样本数据，因此在计算样本方差的时候用N-1。用小样本来估计整体，具体原理可以看无偏估计，极大似然估计。
7.方差：
；每一个样本与期望的偏离程度；
8.样本方差：知道期望值可以求出方差，但是一般情况下，只能得到固定的样本数据，不能准确得到这些数据发生的概率，不能计算期望，只能计算均值，因此我们大多数计算的都是样本方差!!!!!!;样本方差与均值有关；用均值估计期望，用样本方差估计方差；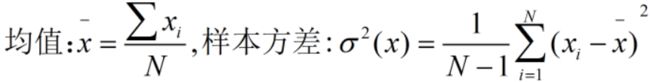
9.中央极限定理：大量的相互独立（各自产生不受到别人的影响）随机变量的均值经标准化后收敛于正态分布；表明了若有独立同分布的随机变量，不管各自的分布如何，只要n足够大，随机变量之和服从于正态分布；我们常用高斯噪声，因为它的概率密度函数服从正态分布，一般在信号噪声分析，图像噪声处理等，都假定为高斯噪声，知道期望方差，就可以计算。然而期望往往计算为平均值，更加简单；这个定理会让我们在数据处理中考虑用高斯函数表示数据分布，这会假定数据是独立同分布的，假定数据是高斯分布的，不同类别的数据指的是具有不同的方差和期望；
10.协方差（标准协方差=相关系数）：不同的PDF具有不同的随机变量。我们知道相同PDF的随机变量的方差，那么不同的随机变量的总体误差称为协方差。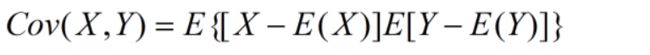
当cov(x,y)>0,x>E(x),y>E(y)的时候x,y正相关，cov(x,y)<0,x
；当我们无法求出数据的期望的时候，就用均值代替。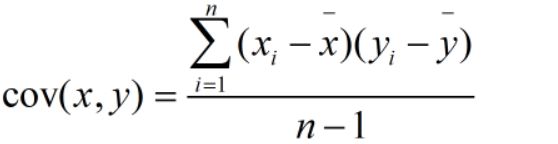
11.协方差矩阵:方差是对应于一维数据的，一维数据用通俗的话讲，就是单个属性，多个样本，每一个样本只有一个属性，我们可以计算这个属性的均值与方差来描述它，当一个随机变量具有多个维度，即一个样本具有多种属性，我们可以计算单个属性的方差，也可以计算不同属性之间的方差判断这些属性之间是否有一定的联系，因此需要协方差矩阵，协方差矩阵中每一个元素是对应两两属性的样本方差；协方差矩阵怎么求？首先：在计算协方差矩阵的时候，一定要判断每一个样本占一行还是占一列。若每一个样本占一行，那么不同列就是不同属性，协方差计算的是不同列之间，即不同属性的关系。下面的计算，每一行代表一个样本。
从上面式子可以得出，协方差对角线是计算每一个属性的样本方差。cov(c2,c1)=cov(c1,c2)
得到协方差矩阵的具体步骤：首先计算c1,c2,…cn的均值。
之后将X 的每一列减去对应的均值。
然后
。
12.联合概率分布函数:也称为多维分布函数，随机向量的分布函数，（x,y）表示坐标，那么F(x,y)的值就是随机点(x,y)落在以点（x,y）为顶点且位于该点左下方无穷矩形区域内的概率；这两个变量中存在线性关系，可以互相表达；
13.概率分布模型：一个随机实验结果，可以根据他的性质来确定模型，比如投硬币正反面，婴儿性别用伯努利，出厂钢钉的误差可以用正态分布等,下面主要介绍几种常见的分布模型，以及含义。
14.伯努利分布：离散；用于只有两个可能的结果1或0；1的概率为p,0的概率为（1-p）第k次成功的伯努利概率质量函数PMF为：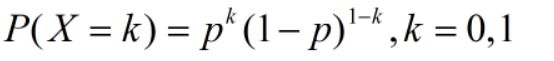
，期望:p,方差:p(1-p)
15.二项分布：离散；n次实验的伯努利分布，当n=1的时候，就是伯努利分布，期望np,方差np(1-p);
16几何分布：离散；独立重复实验，成功概率为p,进行n次成功，前n-1次失败，那么PMF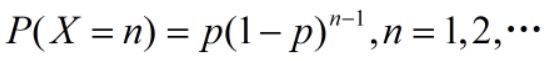
，期望为1/p，方差为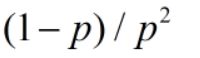
17泊松分布：离散；单位时间内发生的次数可以用泊松分布刻画，例如某段高速公路一年内的交通事故数，办公室一天接到电话的次数，PMF，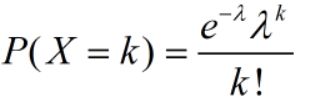
，
表示单位时间内随机事件的平均发生率。
18.指数分布：连续；元器件随着时间寿命减短，类似这种不断衰减的事件，采用指数分布。概率密度函数PDF：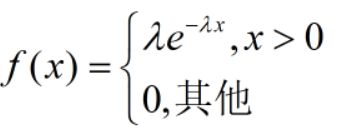
，期望：
，方差：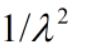
概率分布函数CDF：
19.正态分布：连续；误差产生主要集中在一定的区间，例如信道噪声，工艺钉子误差，经常描述误差；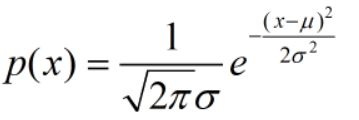
20.均匀分布：在一定区间内，随机变量落在次区间内的概率相同。
21无偏估计：估计量的数学期望等于被估计参数的真实值；假如X1,X2，…Xn样本是来自正态分布总体
，
是均值，则有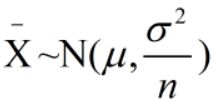
。
22.蒙特卡罗采样：当解决的问题可以转化求解随机分布特征数：概率，期望等，采用蒙特卡罗采用；主要思想，已知一个CDF，求出它的反函数，获取随机变量值，采样后的随机变量的分布接近CDF函数；