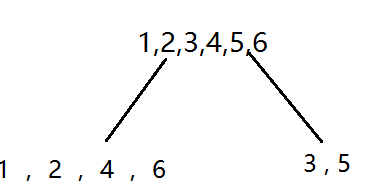后缀自动机的理解

后缀自动机的预备知识

      在字符串算法中，有名叫后缀自动机的算法。它的主要功能有：识别任何一个子串，每个子串出现的次数。算法的逻辑思想很巧妙，在明白字母树后，还有posend（末尾位置）集合等新的知识。

position end set (posend)

      一个字符串S ， 和它的某个子串 。子串在S中会出现n次 ，取子串的最后（end）一个字符在S出现的位置（position）作为集合（set）的元素，这个集合就叫做posend(下面会详细介绍)。

      比如，S = aababa , 子串=ba。那么posend（ba） = {4 ,6}（下标从1开始）。

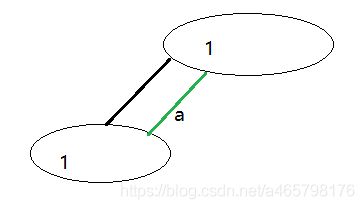
dfa图

      后缀自动机并不是一颗数，而是一个图，这里我简单介绍下dfa图。

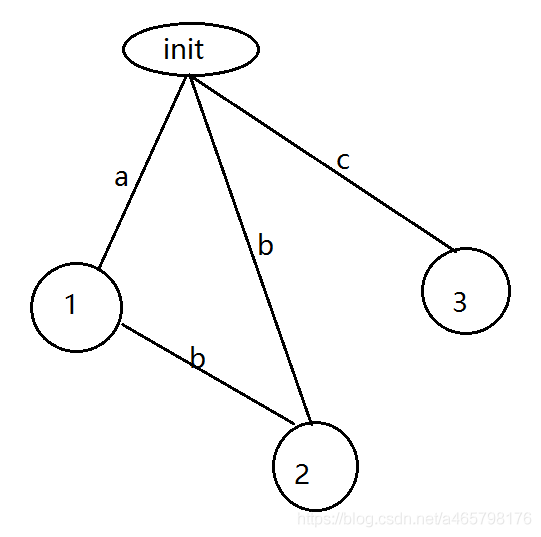
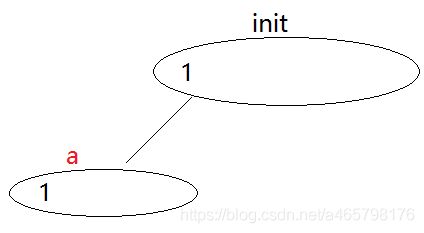
图1

1. 边表示字母。
2. 点表示状态，这个状态可以认为是否存在某个子串。
3. 从initi出发，能走到某个点叫做accept。

position end set (posend)详解

      后缀自动机中会通过position end set 的性质构造一个parent树，这颗树是整个后缀自动机的核心，也是难点。

引理1 如果字符串a是字符串b的后缀 ， 那么posend(b) $⊑$ posend(a)

例子：aababa

• posend(“a”) = {1 , 2 , 4 , 6}
• posend(“ba”) = {4 , 6}
• posend(“ba”) = {4 , 6}$⊑$posend(a)
• 证毕。手动滑稽
  这个引理应该很好想，“ba”出现的位置 “a”一定出现的了，而“a”出现的位置“ba”不一定出现。

图解

图2

引理2 posend(s) 唯一 ，而arcposend( posend(s) ) 并不唯一

例子：aababa

• posend(“ab”) = {3 , 5}
• posend(“b”) = {3 , 5}
• posend(“ab”) = posend(“b”);
• 证毕。手动滑稽
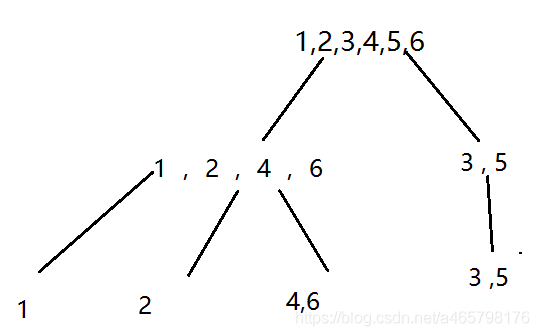
  这个引理实在不知道怎么解释。如图2， b ,a只在这些位置出现那么posend(a) = posend(a)

引理3 arcposend( set )所确定的字符串，是一些长度（字符串的长度）连续的字符串，并且长度短的是长度长的后缀。

例子：aababa

• acrposend({3 , 5}) = “ab” , “b”.
• "b"是“ab”的后缀串
• acrposend({4 , 6}) = “aba” , “ba”.
• "ba"是“aba”的后缀串
• 证毕。手动滑稽

一些长度（字符串的长度）连续的字符串

意思是 反函数所得到的 字符串，他们的长度一定是连续的比如2 ，1；3，2。是不可能出现3，1这种情况

并且长度短的是长度长的后缀

意思是 如果出现了aaaaaaaaaa ,那么就可能出现aaaaaaaaa , aaaaaaaa，aaaaaaa，aaaaaa ，aaaaa，aaaa，aaa，aa，a。
（凑字数的好时机）

引理4 当a,b不是后缀关系时，posend（a） != posend( b )

例子：aababa

• posend(“ba”) = {4,6}.
• posend(“aa”) = {2}.
• posend(“ba”) != posend(“aa”)
• 证毕。
  如果strlen(a) < strlen(b) , 并且posend(a) 与posend(b)有交集。那么在原串中必然存在存在，如图4,那么a就是b的后缀了，与原命题矛盾。
  
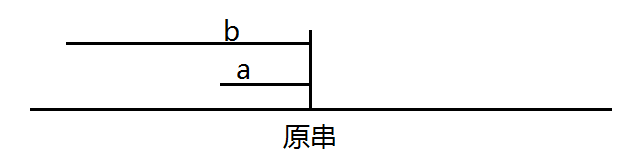
  图4

引理5 由引理1， 2 ， 3 ，4 。可以将全集，通过是否是后缀关系，构造一个parent树。

全集代表着posend("") = {1,2,3,4,5,6…n}
例子：aababa

• 从最简单的"a" ，"b"开始划分posend(“a”) = { 1 ， 2 ， 4 ， 6} ，posend(“b”) = { 3 , 5}.

解释为什么选"a" ，"b

1. 由引理1可知，strlen(s)越小，posend(s)的越大，所以posend(”a“) ，pos(“b”)是最接近全集
2. 由引理4可知，取不相等的字符其posend()无交集
3. 综上， posend(“a”) = { 1 ， 2 ， 4 ， 6} ，posend(“b”) = { 3 , 5}.可完全划分全集。

• 
• 在选以"a"和”b“为后缀的子串#a , aa , ba , ab 。

#a的意思是前面没有了orz

3,5重复了，就把他们变成一个

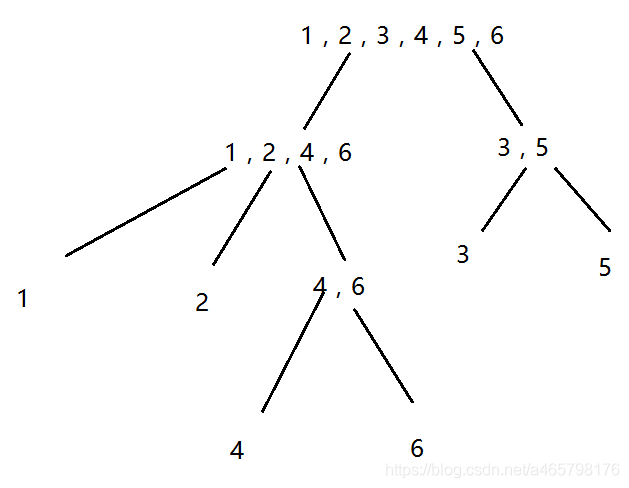
• 最后分好的树如图5所示，是由
• aababa
  1. 第三次#aa ， aba , aab , bab。
  2. 第四次aaba , #aab , abab。
  3. 第五次#aaba , aabab。
  4. 第六次#aabab。
     -
• 图5
  每个节点表示能接受（识别）acrposend({set})的字符串，如下图6
  
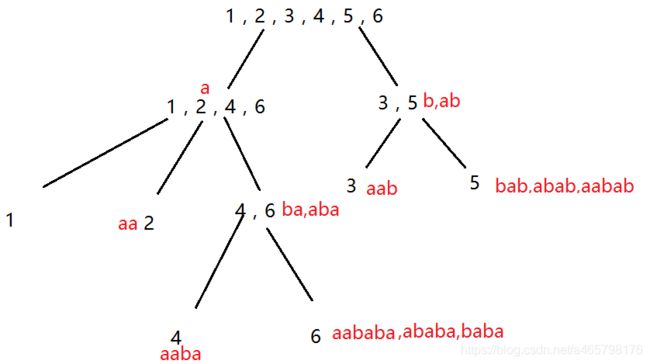
  图6

  引理6 由引理3可知,一的节点Node , 其父节点parent,有字符串长度min_node = max_parent + 1。

如图6，可以很直观的观察到acrposend(Node)所确定的串的长度为[max_node , min_node],和acrposend(parent)所确定的串的长度为[max_parent , min_parent],min_node = max_parent + 1。这个引理6 想表达的逻辑是 一个子串长度越长，它所对应的posend集合可能会变短。当子串的长度到达改变posend集合时 ，即恰好那个关键点，就变成儿子了

这个引理还透露着一些人生哲理

在线构造parent树

众所周知，后缀自动机是Online构造的，上面阐述的静态构造，那么如何Online构造呢？先不考虑代码如何实现，纯大脑暴力。

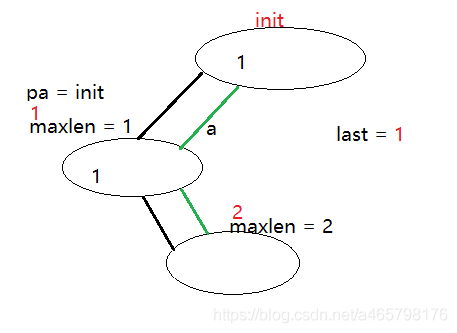
第一步，一个init节点

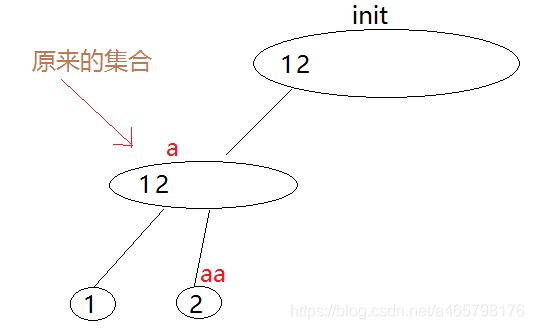
第二步，加入aababa 的 a(下标从1开始)

第三步，aababa加入a

这时理解成加入aa ,a，即arcposend({2})能表示的所有子串，如下图。

• 沿着能绝对表示aa ,a的后缀的节点走。
• 会发现 原来的集合可以包含是aa ,a 但不能包含aa。
• 剔除a ，接下再找aa的位置。
• 而aa和a有是后缀关系。
• 所以，aa所属的集合一定是儿子节点。
  

那为什么不改变 原来的存在能识别的内容呢？如把 a , 变成能识别 a，aa。
答：我讲不通，可以自己体会下
为什么理解成加入aa ,a，即arcposend({2})能表示的所有子串。
答：因为要加的只能是2 这个元素，而这个元素所涉及的就是arcposend({2})

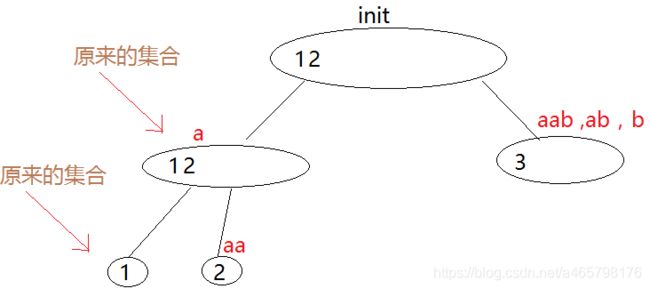
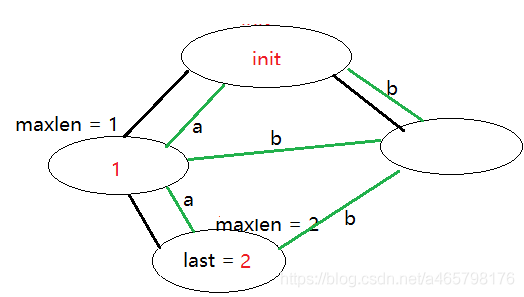
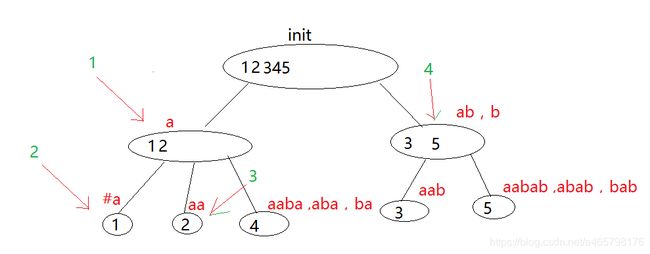
第四步，aababa加入b

加入aab ,ab，b,即arcposend({3})能表示的所有子串，如下图。

• 沿着能绝对表示aab ,ab，b 的后缀的节点走
• 发现没有节点可以走，所以直接创建一个节点
  

第五步，aababa加入a

加入aaba ,aba，ba, a ,即arcposend({4})能表示的所有子串，如下图。

• 沿着能绝对表示aaba ，aba，ba，a 的后缀的节点走。
• 绿色标记的1节点可以绝对表示aaba ，aba，ba，a的后缀，并还匹配a
• 于是走到1 节点 ， 剔除a ， 接着找aaba ，aba，ba。
• 没有找到任何能绝对aaba ，aba，ba的后缀的节点，即2 ，3 不行。
• 于是新建一个。
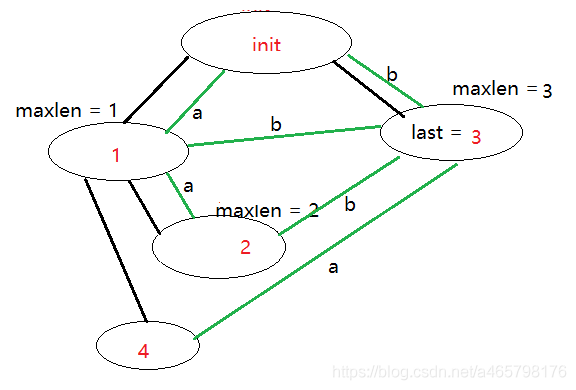
  ## 第六步，aababa加入b
  加入aabab ,abab，bab, ab,b ,即arcposend({4})能表示的所有子串，如下图。
• 沿着能绝对表示aabab ,abab，bab, ab,b 的后缀的节点走。
• 绿色标记的1节点可以绝对表示aabab ,abab，bab, ab,b的后缀
• 发现4节点中的ab,b可以表示,但aab不行
• 于是将4 节点 ，分为两个节点，一个是只表示ab，b，和其子节点aab.
• 剔除ab ,b ，接下再找aabab ,abab，bab的位置。
• 没有找到任何能绝对aabab ,abab，bab的后缀的节点.
• 于是新建一个。
  

在这里解释下绝对二字，即必须完完全全符合。

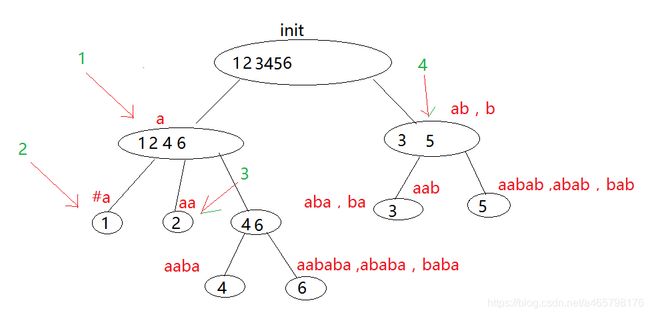
第七步，aababa加入a

加入aababa ,ababa，baba, aba,ba ,a即arcposend({4})能表示的所有子串，如下图。

• 没有知识点了
  

总结

在线加入有3种情况，加入的串设为set1，将加入的节点说表示的串set2

1. set1 == set2 ， 直接加入
2. set1 > set2 , 且 set2 $⊑$ set1,那么剔除set2中串 ， 接着找set1 - set2
3. set1 > set2 ,set1与set2有交集但set2 $⊑$ set1,，把set2变成两个集合set3 , set4.然后找set1 - set3

加入的串与上层有关

• 加入a：a
• 加入a：aa ,a
• 加入b：aab ,ab，b
• 加入a：aaba ,aba，ba, a
• 加入b：aabab ,abab，bab, ab,b
• 加入a：aababa ,ababa，baba, aba,ba ,a
  第n层的集合 = 第n - 1 层的集合 + 第n层的集合要加入的串。

上述构造的树就是后缀数的节点 ， 希望得到的边是 —沿着边走能正好走到节点所表示的串，如下图所示

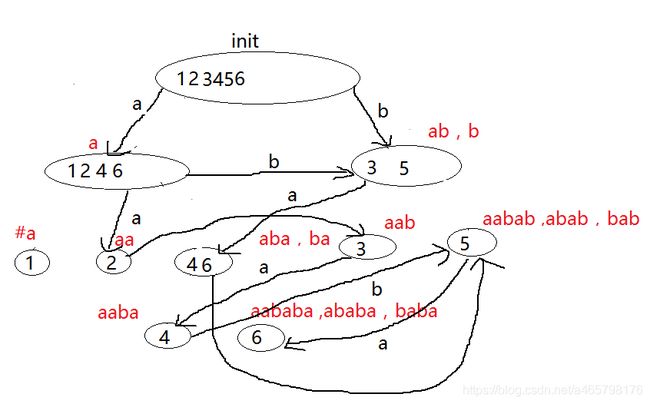
在线构造后缀自动机

在线构造后缀自动机，其实就是在线构造点和边 ， 边分为两种，一种是parent边 ， 即树边 。 一种是出边，即字母边，非树边。

加入的串与上层有关

• 加入a：a
• 加入a：aa ,a
• 加入b：aab ,ab，b
• 加入a：aaba ,aba，ba, a
• 加入b：aabab ,abab，bab, ab,b
• 加入a：aababa ,ababa，baba, aba,ba ,a
  第n层的集合 = 第n - 1 层的集合 + 第n层的集合要加入的串。

由上述规律得：当要加入n元素时，只需和n-1元素所在的集合打交道
例如：
加入6（a）：aababa ,ababa，baba, aba,ba ,a。只需要和含5的集合打交道

如果直接给这些点一个出边，所指向的集合一和set1:{aababa ,ababa，baba, aba,ba ,a}为子集关系
，如下图。

1. 绿色标记的1，2，3点所能识别的字符串集合 和 4成子集关系，并且4的父节点就是（init）。
2. 但是，所打交道的点已经有出边（a）了，那么这个出边所指向的集合和4不一定成子集关系
3. 所以分为两中情况讨论
一， 所指向的集合和4成子集关系，那么4的父节点就是所指向的集合。
二， 所指向的集合和4不成子集关系，那么4定然和这个集合有交集，将交集取出到一个新的节点，这个新的节点就是4的父节点 ， 这个新的节点的父节点就是所指向的节点。

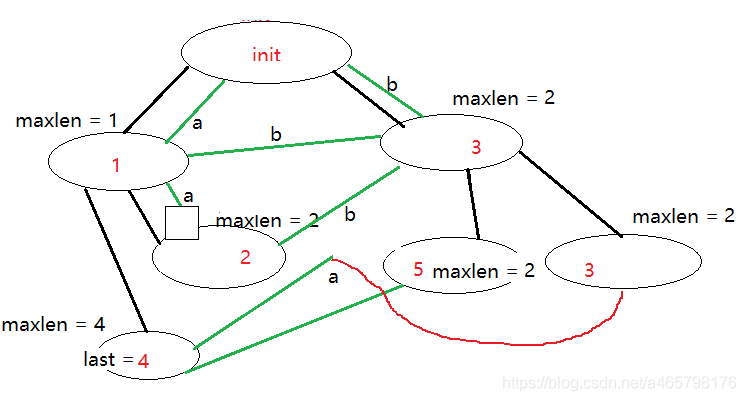
模拟aababa的构造

将上面的总结程序化即

1. 记录c:所要加入的字符 ， 并且创造一个节点new
2. 记录last：上一次加入的最后节点
3. 记录每个节点的maxlen ：acrposend所代表的字符串的最大长度
4. 记录每个节点的parent。
5. 从last开始找。current = last.
6. 查看current 有没有c的出边。
7. case 1 没有 , 则创建c的出边指向new，current = parent(current),重复6 , 至init , parent(new) = init;.
8. case 2 有，且parent(current) 的c出边所指向的节点 node

• maxlen(node) == maxlen(parent(current) ) + 1.
  parent(new) = node，即成子集关系。
• maxlen(node) ！= maxlen(parent(current) ) + 1
  于是把node拆成两部分：
  一部分是 parent(new)+c的字符串集合p，一个其补集，即将成子集关系提取出来。
  parent(补集) = parent(new) = p