金融申请评分卡
金融申请评分卡(1)
金融申请评分卡概念的介绍
目前金融申请评分卡主要使用在一些互联网金融企业和保险银行机构,主要用来解决目前金融机构存在的信用风控问题。
1、信用违约风险的控制手段
从最早的有抵押无规则→无抵押有规则→数据模型,形成了目前在风控领域的基本风控脉络;现今主要采用基于数据驱动建立的风控模型,主要就是目前应用最广泛最多的评分卡模型,评分卡模型主要由分为四种,即:
| 评分卡模型 |
|---|
| 申请评分卡 |
| 行为评分卡 |
| 催收评分卡 |
| 反欺诈评分卡 |
其中最重要的就是金融申请评分卡,目的是把风险控制在贷前的状态;也就是减少交易对手未能履行约定契约中的义务而造成经济损失的风险,里面由包括了个人违约、公司违约、主权违约,这里仅仅只讲到个人违约;
2、个贷中常用的违约定义
- M3&M3+逾期:
这个是最主要的指标,其他指标例如债务重组、个人破产、金融机构主动注销账户、其他相关的违法行为在个贷方面的考虑均不需要过度关注,判断是否逾期主要根据M3&M3+逾期来判断。 - 其他概念性指标:
M0:最后缴款日的第二天到下一个账单日;
M1:M0时段的延续,即在未还款的第二个账单日到第二次账单的最后缴款日之间;
M2:M1的延续,即在未还款的第三个账单日到第二个账单的最后缴款日之间;
3、行业内的一些案例
趣店
趣店CEO罗敏:“凡是过期不还的,我们这里就是坏账,我们的坏账,一律不会催促他们来还钱。电话都不会给他们打。你不还钱,就算了,当作福利送你了”
这方面就反应了趣店对自己的贷前风控非常有把握,同时也说明在前期趣店的利率较高,另外一个方面,因为目前的消费贷场景上,一般贷款的金额较少,追贷成本高,必须要把风控争取控制在贷前。
陆金所CEO表示在2015年11月,行业的坏账率大概在15%-20%之间,2016年1月,已经下降到了13%-17%。
4、评分卡概念
评分卡模型主要有以下这么几个概念:
- 以分数的形式来衡量,这个分数主要根据客户的好坏比来确定;
- 是对未来一段时间内违约/逾期/失联概率的预测
- 有一个明确的正区间
- 通常分数越高越安全
- 数据驱动
- 主要的评分卡模型在互联网金融方面的表现形式是:申请评分卡、反欺诈评分卡、行为评分卡、催收评分卡。
其中申请评分卡、反欺诈评分卡使用在申请环节,行为评分卡使用在监控环节,催收评分卡使用在逾期管理环节。
4.1、申请评分卡
申请评分卡用在申请环节,以申请者在申请当日及过去的信息为基础,预测未来放款后的逾期或者违约的概率。
开发申请评分卡的目的有:
- 可以做风险控制:借贷生命周期的第一个关口就可以把控住优质客户
- 营销:做好优质客户的识别
我们一般预测未来放款后的逾期,这个未来的时间段,在我工作经历当中,一般是一年左右,时间更长就是用行为评分卡,或许在银行等大型机构,因为收集的信息更全面,在评分方面的要求不一样,可能对未来的预测时间也不一样,或许时间会更长。
4.2、申请评分卡的特性
优秀的评分卡应该具备的特性:
1. 稳定性:当总体逾期/违约概率不变,分数的分步也应该没有改变
2. 区分性:违约人群与正常人群的分数应当有显著的差异,具体如下图所示: 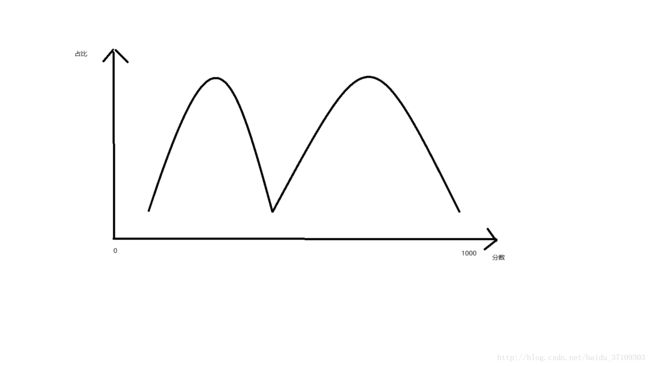
3. 预测能力:低分人群的违约率更高
4. 和逾期概率等价:评分应该可以精准地反应违约/逾期概率,反之亦然
4.3、申请评分卡的开发流程
- 启动:场景、对象、目的
- 数据准备与预处理:账户、客户、内部和外部数据的汇集抽取和清洗
- 模型构建:基本就是逻辑回归,也可能用到集成学习(随机森林是集成学习的特例)
- 模型的评估:区分度、预测性、平稳性(看分数的分步情况)
- 验证/审计:是否有计算错误、逻辑错误、业务错误
- 模型部署:开发环境→生产环境、容量、并发度
- 模型监控:模型性能是不是比较稳定
备注一下:
截止目前,看到的评分卡模型基本都是用逻辑回归开发的,优点比较多,稳定和解释性强,解释性强因为在对比其他分数期间,逻辑回归相对是有多个可加项,可具体比较,SVM就基本做不到,缺点是对数据质量的要求非常高,需要在数据预处理方面花很多的时间,模型的简单但是开发成本并不低;决策树模型方面,对数据质量要求低,也比较容易解释,但是模型的准确度不高;组合模型方面,部署比较麻烦,在评分卡方面应用不是很多。
4.4申请评分卡一般需要的字段
- 个人信息:学历 性别 收入
- 负债能力:在申请的金融机构或者其他金融机构的负债情况(例如月还债金额超过月收入的60%,说明负债较高),例如多投信息等
- 消费能力:商品购买记录,出境游,奢侈品消费
- 历史信用记录:历史逾期行为
- 其他数据:个人交际、网络足迹、个人财务等
备注:客户还款能力*还款意愿 = 还款等级
这里我提供一份数据,其中字段如下:
| 字段 | 名称 |
|---|---|
| member_id | ID |
| loan_amnt | 申请额度 |
| term | 产品期限 |
| int_rate | 利率 |
| emp_length | 工作期限 |
| home_ownership | 是否有自有住宅 |
| annual_inc | 年收入 |
| verification_status | 收入核验状态 |
| desc | 描述 |
| purpose | 贷款目的 |
| title | 贷款目的描述 |
| zip_code | 联系地址邮政编码 |
| addr_state | 联系地址所属州 |
| delinq_2yrs | 申贷日期前2年逾期次数 |
| inq_last_6mths | 申请日前6个月咨询次数 |
| mths_since_last_delinq | 上次逾期距今月份数 |
| mths_since_last_record | 上次登记公众记录距今的月份数 |
| open_acc | 征信局中记录的信用产品数 |
| pub_rec | 公众不良记录数 |
| total_acc | 正在使用的信用产品数 |
| pub_rec_bankruptcies | 公众破产记录数 |
| earliest_cr_line | 第一次借贷时间 |
| loan_status | 贷款状态—目标变量 |
5、评分卡经常遇到的问题
在评分卡模型中,经常遇到的问题就是非平衡样本的问题。在一个样本里面,坏的样本很少或者好的样本很少,导致了数据的不平衡。在处理数据不平衡样本中,一般有三种办法:
- 过采样:方法简单,就是对少的那一部分样本进行重复采样,并且操作简单,对数据质量的要求也低;缺点是容易造成模型的过拟合(例如坏好比例为1:99,为了增大坏的比例,多次采样,将比例调整到10:99,这样非常容易导致模型过拟合);
- 欠采样:优点和过采样类似,缺点是容易造成模型的欠拟合;
- SMOTE:优点是不易过拟合,能够保留大量的信息,缺点是不能对缺失值和类别变量做处理。
SMOTE算法原理:
- 采样最近邻算法,计算出每个少数类样本的K个同类近邻;
- 从K个同类近邻中随机挑选N个样本进行随机线性插值;
- 构造新的少数类样本:
New=Xi+rand(0,1)∗(yj−xi),j=1,2,3,4.....NNew=Xi+rand(0,1)∗(yj−xi),j=1,2,3,4.....N
其中XiXi为少类中的一个观测点,YjYj为K个近邻中随机抽取的样本 - 将新样本与原数据合成,产生新的训练集
例子:选取了一个X1X1为年龄为22岁,月收入为8000元,则X1=(22,8000)X1=(22,8000),选取了一个近邻点为X2X2,X2=(28,5000)X2=(28,5000),随机系数为0.5,计算逻辑为22+(28−22)∗0.5=25,8000+(5000−8000)∗0.5=650022+(28−22)∗0.5=25,8000+(5000−8000)∗0.5=6500,这样得到的一个新的X3X3点为(25,6500)
(25,6500)。
金融申请评分卡的数据预处理和特征衍生
1、模型处理的一般流程
以上为模型的一般处理办法;在本次数据字段有:
| 字段 | 名称 |
|---|---|
| member_id | ID |
| loan_amnt | 申请额度 |
| term | 产品期限 |
| int_rate | 利率 |
| emp_length | 工作期限 |
| home_ownership | 是否有自有住宅 |
| annual_inc | 年收入 |
| verification_status | 收入核验状态 |
| desc | 描述 |
| purpose | 贷款目的 |
| title | 贷款目的描述 |
| zip_code | 联系地址邮政编码 |
| addr_state | 联系地址所属州 |
| delinq_2yrs | 申贷日期前2年逾期次数 |
| inq_last_6mths | 申请日前6个月咨询次数 |
| mths_since_last_delinq | 上次逾期距今月份数 |
| mths_since_last_record | 上次登记公众记录距今的月份数 |
| open_acc | 征信局中记录的信用产品数 |
| pub_rec | 公众不良记录数 |
| total_acc | 正在使用的信用产品数 |
| pub_rec_bankruptcies | 公众破产记录数 |
| earliest_cr_line | 第一次借贷时间 |
| loan_status | 贷款状态—目标变量 |
2、数据的预处理
2.1、基本处理办法
- 利率方面的处理办法:带%的百分比,需要转化为浮点数
- 工作年限“<1 year”转化为0,“>10 year”的转化为1
- 日期方面:直接转化为标准日期
- 文本信息:字段中的desc就是客户申请期间的申请原因等信息,这里处理采用最简单的办法,如果里面有信息,则为1,无信息则为0,其他例如采用NLP的办法,做其他处理,暂时不做,因为涉及分词等等,处理其他麻烦,不是写这次博客的主要目的。
2.2、缺失值的处理办法
缺失值的种类情况:
- 完全随机缺失
- 随机缺失
- 完全非随机缺失
处理的办法一般为以下几种:
- 补缺
- 作为一种状态,例如,空的为0,非空为1,处理起来简单,如果缺失值不多,效果不错
- 删除本行的记录,这种处理办法最简单,尤其在数据量较大的情况下,删除部分数据,对整体基本无影响。
2.3、数据特征构-特征衍生
因为在原有的特征上面,也就是直接特征方面的信息含量不足以很好的建立申请评分卡模型,所以一般都会去构建新的特征,进行特征的衍生。那么经常接触到的特征衍生办法如下:
- 计数:过去1年内申请贷款的总次数
- 求和:过去1年内的在线上的消费金额
- 比例:贷款申请额度和年收入的占比
- 时间差:第一次开户距离今天的时间长度
- 波动率:过去3年内每份工作的时间的标准差
以上构建的办法均基于经验的构建,不包含了因子分析等办法
2.4、特征的分箱
特征分箱的目的:
- 将连续变量离散化
- 将多状态的离散变量合并成少状态
分箱的通俗解释:
- 稳定性:避免了特征中的无意义的波动对评分带来的不好的影响
- 加强了模型的健壮性:避免了模型受到极端值的影响
举个例子:例如未进行分箱之前,样本数据里面没有一个高二年级的学生,那么假定做好分箱之后,高一到高三均属于高中,因此出现一个高二年级的学生后,就会被划入高中这个“箱”,模型的稳定性就得到了加强;在健壮性方面,例如我的收入是1000,在申请贷款的时候给予的评分很低,假定就20分,经过我的不断努力,跳槽7-8次之后,薪水涨到1500左右,这个时候,还是属于低收入的困难人群,那么给予的评分还是20分左右,这样模型的健壮性就得到了体现,模型不需要根据一些小的变化就进行调整。
分箱简单的解释是:分箱就是为了做到同组之间的差异尽可能的小,不同组之间的差异尽可能的大。
分箱的好处:
- 可以把缺失值作为一个独立的箱带入到模型中去
- 将所有的变量变换到相似的尺度上(例如:一个变量是年龄,一个变量是月收入,不做分箱,2者之间的变化差距太大)
分箱的缺点:
- 计算量比较大,处理数据过程较为繁琐。
- 编码之后容易导致信息的丢失。
2.5、特征的分箱方法
分箱的办法主要接触到很多,等距、等频、卡方分箱、决策树分箱法,这里只具体展示卡方分箱法,决策树分箱的代码如下,其他的分箱仅说明原理:
coding=utf-8
import operator
from math import log
import time
class InformationGainSplitDiscretization(object):
def __init__(self):
self.minInfoGain_epos = 1e-8 #停止条件之一:最小信息增益,当某数据集的最优分裂对应的信息增益(即最大信息增益)小于这个值,则此数据集停止进一步的分裂。
self.splitPiontsList = [] #分裂点列表,最终要依分裂点的值升序排列。以便后续的离散化函数(输入:待离散的数据集)使用。 #self.totalGain = ()
self.tree_deep = 3
def splitDataSet(self,dataSet, splitpoint_idx):
leftSubDataSet = []
rightSubDataSet = []
for leftSubSet in dataSet[:(splitpoint_idx+1)]:
leftSubDataSet.append(leftSubSet)
for rightSubSet in dataSet[(splitpoint_idx+1):]:
rightSubDataSet.append(rightSubSet)
leftSubDataSet.sort(key=lambda x : x[0], reverse=False)
rightSubDataSet.sort(key=lambda x : x[0], reverse=False)
return (leftSubDataSet,rightSubDataSet)
def calcInfoGain(self,dataSet):
lable1_sum = 0
total_sum = 0
infoGain = 0
if dataSet == []:
pass
else :
for i in range(len(dataSet)):
lable1_sum += dataSet[i][1]
total_sum += dataSet[i][1] + dataSet[i][2]
p1 = (lable1_sum*1.0) / (total_sum*1.0)
p0 = 1 - p1
if p1 == 0 or p0 == 0:
infoGain = 0
else:
infoGain = - p0 * log(p0) - p1 * log(p1)
return infoGain,total_sum
def getMaxInfoGain(self,dataSet):
gainList = []
totalGain = self.calcInfoGain(dataSet)
maxGain = 0
maxGainIdx = 0
for i in range(len(dataSet)):
leftSubDataSet_info = self.calcInfoGain(self.splitDataSet(dataSet, i)[0])
rightSubDataSet_info = self.calcInfoGain(self.splitDataSet(dataSet, i)[1])
gainList.append(totalGain[0]
- ((leftSubDataSet_info[1]*1.0)/(totalGain[1]*1.0)) * leftSubDataSet_info[0]
- ((rightSubDataSet_info[1]*1.0)/(totalGain[1]*1.0)) * rightSubDataSet_info[0])
maxGain = max(gainList)
maxGainIdx = gainList.index(max(gainList))
splitPoint = dataSet[maxGainIdx][0]
return splitPoint,maxGain,maxGainIdx
def getSplitPointList(self,dataSet,maxdeeps,begindeep):
if begindeep >= maxdeeps:
pass
else:
maxInfoGainList = self.getMaxInfoGain(dataSet)
if maxInfoGainList[1] <= self.minInfoGain_epos:
pass
else:
self.splitPiontsList.append(maxInfoGainList[0])
begindeep += 1
subDataSet = self.splitDataSet(dataSet, maxInfoGainList[2])
self.getSplitPointList(subDataSet[0],maxdeeps,begindeep)
self.getSplitPointList(subDataSet[1],maxdeeps,begindeep)
def fit(self, x, y,deep = 3, epos = 1e-8):
self.minInfoGain_epos = epos
self.tree_deep = deep
bin_dict = {}
bin_list = []
for i in range(len(x)):
pos = x[i]
target = y[i]
bin_dict.setdefault(pos,[0,0])
if target == 1:
bin_dict[pos][0] += 1
else:
bin_dict[pos][1] += 1
for key ,val in bin_dict.items():
t = [key]
t.extend(val)
bin_list.append(t)
bin_list.sort( key=lambda x : x[0], reverse=False)
self.getSplitPointList(bin_list,self.tree_deep,0)
self.splitPiontsList = [elem for elem in self.splitPiontsList if elem != []]
self.splitPiontsList.sort()
def transform(self,x):
res = []
for e in x :
index = self.get_Discretization_index(self.splitPiontsList, e)
res.append(index)
return res
def get_Discretization_index(self, Discretization_vals, val):
index = len(Discretization_vals) + 1
for i in range(len(Discretization_vals)):
bin_val = Discretization_vals[i]
if val <= bin_val:
index = i + 1
break
return index- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
无监督分箱方法(一般不推荐,好不好用,得看人品,一般比卡方和决策树的效果要差点)
等距划分:
从最小值到最大值之间,均分为 N 等份, 这样, 如果 A,B 为最小最大值, 则每个区间的长度为 W=(B−A)/N , 则区间边界值为A+W,A+2W,….A+(N−1)W 。这里只考虑边界,每个等份里面的实例数量可能不等。等频分箱:
区间的边界值要经过选择,使得每个区间包含大致相等的实例数量。比如说 N=10 ,每个区间应该包含大约10%的实例。比较:
比如,等宽区间划分,划分为5区间,最高工资为50000,则所有工资低于10000的人都被划分到同一区间。等频区间可能正好相反,所有工资高于50000的人都会被划分到50000这一区间中。这两种算法都忽略了实例所属的类型,落在正确区间里的偶然性很大。
对特征进行分箱后,需要对分箱后的每组(箱)进行woe编码,然后才能放进模型训练。
有监督分箱方法
Best-KS(非常类似决策树的分箱,决策树分箱的标准是基尼指数,这里就只考虑KS值):
让分箱后组别的分布的差异最大化。
步骤:对于连续变量- 排序
- 计算每一点的KS值
- 选取最大的KS值对应的特征值,用该特征值将特征分为大于该值和小于该值两端
- 对于每一部分,循环b、c步骤,直到满足终止条件
终止条件,继续回滚到上一步:
- 下一步分箱,最小的箱的占比低于设定的阈值(0.05)
- 下一步分箱后,有一箱的对应的y的类别全部为0或者1
- 下一步分箱后,bad rate不单调
步骤:对于离散很高的分类变量
- 编码(类别变量个数很多,先编码,再分箱。)
- 依据连续变量的方式进行分箱
分箱以后变量必须单调,具体的例子如下图: 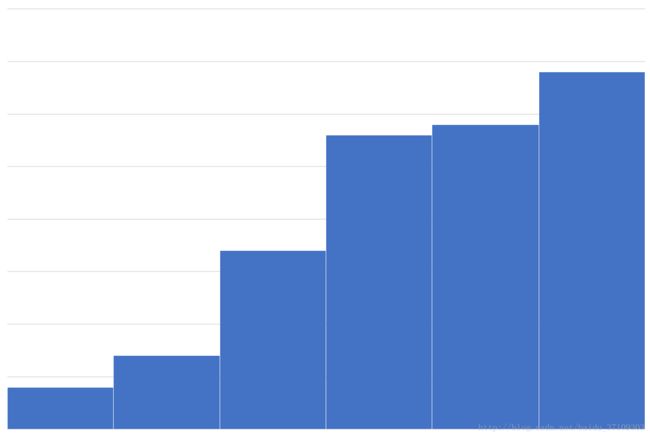
假定变量被分成了6个箱,假定X轴为年龄,Y轴为坏样本率,这样就可以解释了,年龄越大,坏客户的比例约多。如果分箱之后不单调,那么模型在这个变量上的可解释性就成问题了。所以在分箱期间要注意变量的单调性。
卡方分箱:
这里copy一段官方解释(比较长):自底向上的(即基于合并的)数据离散化方法。它依赖于卡方检验:具有最小卡方值的相邻区间合并在一起,直到满足确定的停止准则。通俗的讲,即让组内成员相似性强,让组间的差异大。基本思想:对于精确的离散化,相对类频率在一个区间内应当完全一致。因此,如果两个相邻的区间具有非常类似的类分布,则这两个区间可以合并;否则,它们应当保持分开。而低卡方值表明它们具有相似的类分布。
忘记上面,直接实践一下,步骤如下:
- 预先我们设定一个卡方的阈值
- 根据离散化的属性对实例进行排序,每个实例属于一个区间
- 开始合并,具体分2步:
- 计算每一对相邻区间的卡方数值
- 卡方值最小的一对区间直接合并
X2=∑i=12∑j=12(Aij−Eij)2EijX2=∑i=12∑j=12(Aij−Eij)2Eij
AijAij:第i区间第j类的实例的数量
Eij:AijEij:Aij的期望频率,为Ni×CjNNi×CjN,N是总样本,NiNi是第i组的样本数,CjCj是第j类样本在全体中的比例
接下来就百度一下卡方检验阈值,直接看里面的数值,找到显著水平和自由度,自由度为2,90%置信度的情况下,卡方为4.6;如果忘记了卡方检验的意义,直接百度卡方检验。
目前一般分箱5个或者6个,置信度在0.95左右,区间为10-15之间。主要是因为分箱太多,操作起来太麻烦,对模型的提高也不大,分箱5个一般就不错。
卡方分箱的终止条件很简单,基本就是2条:
- 默认分到多少箱,如果已经分到了这个数值了,那就第2步
- 检查一下单调性,满足就完成分箱了,如果不满足,相邻的箱就合并,直到单调了为止,因为最后合并到2个箱的时候,是一定单调的。
- 补充:分箱之前要切分,通常50-100个切分点,看数据量的大小,最最最重要的,千万不要用等距划分,因为比如收入、年龄这些字段成偏态分步,数据没有平均分布,要用等频划分。
- 类别变量,类别较少,就不用在分箱了,如果有那个类别是全部为坏样本,需要和最小的不是坏样本的合并一下,因为不合并等会WOE不能计算了。
- 最后补充:在评分卡模型中,能不用热编码就不要用热编码,因为热编码膨胀了数据量,在选择变量是不是进入模型当中去,也是存在问题了,例如逐步回归就不好搞,业务方面的解释性也差,没直接的业务逻辑关系。总之,能不用就不用,要是没变量了,还是可以考虑用一下。
3、WOE编码
WOE编码官方解释:一种有监督的编码方式,将预测类别的集中度的属性作为编码的数值;优势是:将特征的值规范到相近的尺度上。缺点是:需要分箱后每箱都同时有好坏样本(例如,预测违约和不违约可是使用WOE编码,如果去预测中度违约、重度违约、轻度违约等等情况,这个时候WOE编码就不行了)。通常意义上,WOE的绝对值在0.1-3之间。
编码的意义在于符号与好样本的比例有关;当好样本为分子,坏样本为分母的时候,可以要求回归模型的系数为负。
具体的WOE编码这里就不找材料了,CSDN博客上,有很多写的很好的,这里引用一篇博客在这里,请猛击。
这里简单引用一下其他人成熟的比较正式说法,WOE公式如下:
例如,以年龄作为一个变量,由于年龄是连续型自变量,需要对其进行离散化处理,假设离散化分为5组(如何分箱,上面已经介绍,后面将继续介绍),#bad和#good表示在这五组中违约用户和正常用户的数量分布,最后一列是woe值的计算,通过后面变化之后的公式可以看出,woe反映的是在自变量每个分组下违约用户对正常用户占比和总体中违约用户对正常用户占比之间的差异;从而可以直观的认为woe蕴含了自变量取值对于目标变量(违约概率)的影响。再加上woe计算形式与logistic回归中目标变量的logistic转换(logist_p=ln(p/1-p))如此相似,因而可以将自变量woe值替代原先的自变量值;,具体的计算情况如下:
| Age | bad | good | WOE |
|---|---|---|---|
| 0-10 | 50 | 200 | =ln((50/100)/(200/1000))=ln((50/200)/(100/1000)) |
| 10-18 | 20 | 200 | =ln((20/100)/(200/1000))=ln((20/200)/(100/1000)) |
| 18-35 | 5 | 200 | =ln((5/100)/(200/1000))=ln((5/200)/(100/1000)) |
| 35-50 | 15 | 200 | =ln((15/100)/(200/1000))=ln((15/200)/(100/1000)) |
| 50以上 | 10 | 200 | =ln((10/100)/(200/1000))=ln((10/200)/(100/1000)) |
| 汇总 | 100 | 1000 |
4、IV值
IV值的官方解释为:IV(Information Value), 衡量特征包含预测变量浓度的一种指标。
计算公式如下:
| Age | bad | good | iv |
|---|---|---|---|
| 0-10 | 50 | 200 | =(50/100-200/1000)*ln((50/100)/(200/1000))=IV1IV1 |
| 10-18 | 20 | 200 | =(20/100-200/1000)*ln((20/100)/(200/1000))=IV2IV2 |
| 18-35 | 5 | 200 | =(5/100-200/1000)*ln((5/100)/(200/1000))=IV3IV3 |
| 35-50 | 15 | 200 | =(25/100-200/1000)*ln((15/100)/(200/1000))=IV4IV4 |
| 50以上 | 10 | 200 | =(10/100-200/1000)*ln((10/100)/(200/1000))=IV5IV5 |
| 汇总 | 100 | 1000 | IV汇总IV汇总 =IV1IV1+IV2IV2+IV3IV3+IV4IV4+ IV5IV5 |
IV汇总IV汇总就得到了这个变量的总体IV值。
金融申请评分卡样例及代码
- 数据文件中的所有对应的字段,在金融申请评分卡(2)均有解释,数据的下载链接为百度网盘:链接:https://pan.baidu.com/s/1qZXmYgW 密码:r6o5
- 代码情况如下,尽可能在每段代码均有解释,具体的代码如下:
# -*- coding: utf-8 -*-
@author: Gupeng
#这段加载所需要的数据包
import numpy as np
import pandas as pd
import re
import time
import datetime
from dateutil.relativedelta import relativedelta
from sklearn.model_selection import train_test_split
#读取所有的数据
allData = pd.read_csv(r'C:/Users/Sam/Desktop/data.csv',header = 0)
#把月份后面的months替换成空,方便后期处理(数据在外面下载的,如果是大家在数据库里面取出来,没这样乱七八糟)
allData['term'] = allData['term'].apply(lambda x: int(x.replace(' months','')))
# 处理标签:Fully Paid是正常用户;Charged Off是违约用户
allData['y'] = allData['loan_status'].apply(lambda x: int(x == 'Charged Off'))
#这里有个重点,产品期限不能太长,申请评分卡模型评估的违约概率必须在统一的期限中,所以就选个期限为36的
allData1 = allData.loc[allData.term == 36]
#切割数据
trainData, testData = train_test_split(allData1,test_size=0.4)
#接下来,开始数据预处理
#处理一下百分号,把百分号改为浮点
trainData['int_rate_clean'] = trainData['int_rate'].map(lambda x: float(x.replace('%',''))/100)
#把工作年限强制处理一下,防止影响排序
def Year(x):
if x.find('n/a') > -1:
return -1
elif x.find("10+")>-1:
return 11
elif x.find('< 1') > -1:
return 0
else:
return int(re.sub("\D", "", x))
trainData['emp_length_clean'] = trainData['emp_length'].map(Year)
#在处理缺失数据的时候,因为这次数据样本不多,全删除不现实,直接把缺失作为一种状态,非缺失作为另外一种状态
def DescExisting(x):
x2 = str(x)
if x2 == 'nan':
return 'no desc'
else:
return 'desc'
trainData['desc_clean'] = trainData['desc'].map(DescExisting)
#最后处理一下这个日期,日期方面的处理在python方面比较繁琐,这里也处理一下
def datemanage(x,format):
if str(x) == 'nan':
return datetime.datetime.strptime('9900-1','%Y-%m')
else:
return datetime.datetime.strptime(x,format)
trainData['app_date_clean'] = trainData['issue_d'].map(lambda x: datemanage(x,'%Y/%m/%d'))
trainData['earliest_cr_line_clean'] = trainData['earliest_cr_line'].map(lambda x: datemanage(x,'%Y/%m/%d'))
#处理一下缺失值,把0用-1代替,处理了上次逾期距今月份数、自上次公开记录以来的月数、破产记录数
def MakeupMissing(x):
if np.isnan(x):
return -1
else:
return x
trainData['mths_since_last_delinq_clean'] = trainData['mths_since_last_delinq'].map(lambda x:MakeupMissing(x))
trainData['mths_since_last_record_clean'] = trainData['mths_since_last_record'].map(lambda x:MakeupMissing(x))
trainData['pub_rec_bankruptcies_clean'] = trainData['pub_rec_bankruptcies'].map(lambda x:MakeupMissing(x))
#形成衍生变量,这个需要理解业务,具体处理办法看实际情况
#申请额度占收入的占比
trainData['limit_income'] = trainData.apply(lambda x: x.loan_amnt / x.annual_inc, axis = 1)
#第一次借贷时间到来我方申请日期的跨度,按照月份处理
def MonthGap(earlyDate, lateDate):
if lateDate > earlyDate:
gap = relativedelta(lateDate,earlyDate)
yr = gap.years
mth = gap.months
return yr*12+mth
else:
return 0
trainData['earliest_cr_to_app'] = trainData.apply(lambda x: MonthGap(x.earliest_cr_line_clean,x.app_date_clean), axis = 1)
#接下来,开始使用卡方分箱处理数据
#汇总一下前面的要求:不超过5箱,分好之后变量关联好坏比单调,每箱同时包含好坏样本,特殊值-1这类的,可以单独一箱;
#连续型变量可以直接分箱;如果遇到类别型变量,在类别较多的情况下,需要先进行bad rate编码,再分箱;如果类别少:1、每种类别同时包含好坏样本,无需分箱;2、有类别只包含好坏样本的一种,需要合并。
#数值型变量
num_features = ['int_rate_clean','emp_length_clean','annual_inc', 'dti', 'delinq_2yrs', 'earliest_cr_to_app','inq_last_6mths', \
'mths_since_last_record_clean', 'mths_since_last_delinq_clean','open_acc','pub_rec','total_acc']
#类别型变量
cat_features = ['home_ownership', 'verification_status','desc_clean', 'purpose', 'zip_code','addr_state','pub_rec_bankruptcies_clean']
more_value_features = []
less_value_features = []
#接下来第一步检查类别变量中,那些变量的取值超过5个
for var in cat_features:
valueCounts = len(set(trainData[var]))
print (valueCounts)
if valueCounts > 5:
more_value_features.append(var) #取值超过5的变量,需要bad rate编码,再用卡方分箱法进行分箱
else:
less_value_features.append(var)
#求出每个变量每一箱的bad rate
def BinBadRate(df, col, target, grantRateIndicator=0):
'''
:param df: 需要计算好坏比率的数据集
:param col: 需要计算好坏比率的特征
:param target: 好坏标签
:param grantRateIndicator: 1返回总体的坏样本率,0不返回
:return: 每箱的坏样本率,以及总体的坏样本率(当grantRateIndicator==1时)
'''
total = df.groupby([col])[target].count()
total = pd.DataFrame({'total': total})
bad = df.groupby([col])[target].sum()
bad = pd.DataFrame({'bad': bad})
regroup = total.merge(bad, left_index=True, right_index=True, how='left')
# regroup.reset_index(level=0, inplace=True)
regroup.reset_index(inplace=True) #重建索引
regroup['bad_rate'] = regroup.apply(lambda x: x.bad * 1.0 / x.total, axis=1)
dicts = dict(zip(regroup[col],regroup['bad_rate']))
if grantRateIndicator==0: #如果不等于0,则求出整体的坏的客户占比情况。等于0则只计算到每个变量类别中的坏客户比例。
return (dicts, regroup)
N = sum(regroup['total'])
B = sum(regroup['bad'])
overallRate = B * 1.0 / N
return (dicts, regroup, overallRate)
#目的是让坏样本为0的箱子与其他不为0的进行合并,并且求出变量中的类别属于哪个箱子
def MergeBad0(df,col,target):
'''
:param df: 需要计算好坏比率的数据集
:param col: 需要计算好坏比率的特征
:param target: 好坏标签
:return: WOE 和 IV 的字典
'''
regroup = BinBadRate(df, col, target)[1]
regroup = regroup.sort_values(by = 'bad_rate')
col_regroup = [[i] for i in regroup[col]]
for i in range(regroup.shape[0]-1):
col_regroup[i+1] = col_regroup[i] + col_regroup[i+1]
col_regroup.pop(i)
if regroup['bad_rate'][i+1] > 0:
break
newGroup = {}
for i in range(len(col_regroup)):
for g2 in col_regroup[i]:
newGroup[g2] = 'Bin '+str(i)
return newGroup
#如果类别变量里面有全是坏的就合并,全是好的也合并
# (i)当取值<5时:如果每种类别同时包含好坏样本,无需分箱;如果有类别只包含好坏样本的一种,需要合并
merge_bin_dict = {} #存放需要合并的变量,以及合并方法
var_bin_list = [] #由于某个取值没有好或者坏样本而需要合并的变量
for col in less_value_features: #类别小于5的类别变量
binBadRate = BinBadRate(trainData, col, 'y')[0] #求出了坏的样本的占比
# print(BinBadRate(trainData, col, 'y')[0])
if min(binBadRate.values()) == 0 : #由于某个取值没有坏样本而进行合并
print ('{} need to be combined due to 0 bad rate'.format(col))
combine_bin = MergeBad0(trainData, col, 'y')
merge_bin_dict[col] = combine_bin
newVar = col + '_Bin'
trainData[newVar] = trainData[col].map(combine_bin) #combine_bin是一个对应关系,根据对应关系,将类别变换成对应的箱子
var_bin_list.append(newVar) #需要合并的变量添加到这个列表
if max(binBadRate.values()) == 1: #由于某个取值没有好样本而进行合并
print ('{} need to be combined due to 0 good rate'.format(col))
combine_bin = MergeBad0(trainData, col, 'y',direction = 'good')
merge_bin_dict[col] = combine_bin
newVar = col + '_Bin'
trainData[newVar] = trainData[col].map(combine_bin)
var_bin_list.append(newVar)
#less_value_features里剩下不需要合并的变量 不需要合并处理的变量
def BadRateEncoding(df, col, target):
'''
:param df: 需要计算好坏比率的数据集
:param col: the feature that needs to be encoded with bad rate, usually categorical type
:param target: good/bad indicator
:return: the assigned bad rate to encode the categorical feature
'''
regroup = BinBadRate(df, col, target, grantRateIndicator=0)[1]
#以col作为索引,并且除索引外转化为dict格式
br_dict = regroup[[col,'bad_rate']].set_index([col]).to_dict(orient='index')
#把类别变量里面的类型和坏样本占比对应起来
for k, v in br_dict.items():
br_dict[k] = v['bad_rate']
#将类别变量中的类型替换为怀样本占比
badRateEnconding = df[col].map(lambda x: br_dict[x])
return {'encoding':badRateEnconding, 'bad_rate':br_dict}
#类别变量中的类型超过5个,最后作为一个数值变量添加进去
# (ii)当取值>5时:用bad rate进行编码,放入连续型变量里
br_encoding_dict = {} #记录按照bad rate进行编码的变量,及编码方式
for col in more_value_features:
br_encoding = BadRateEncoding(trainData, col, 'y')
print(br_encoding)
trainData[col+'_br_encoding'] = br_encoding['encoding']
br_encoding_dict[col] = br_encoding['bad_rate']
num_features.append(col+'_br_encoding')